Ах2 вх с что означает с
Урок «Функция y=ax^2+bx+c, её свойства и график»
Краткое описание документа:
Рассмотрим выражение вида ах 2 +вх+с, где а, в, с – действительные числа, а отлично от нуля. Это математическое выражение известно как квадратный трехчлен.
Но не всегда у квадратного трехчлена присутствуют все три слагаемые. Возьмем для примера выражение 3х 2 + 2х, где а=3, в=2, с=0.
Перейдем к квадратичной функции у=ах 2 +вх+с, где а, в, с – любые произвольные числа. Эта функция является квадратичной, так как содержит член второй степени, то есть х в квадрате.
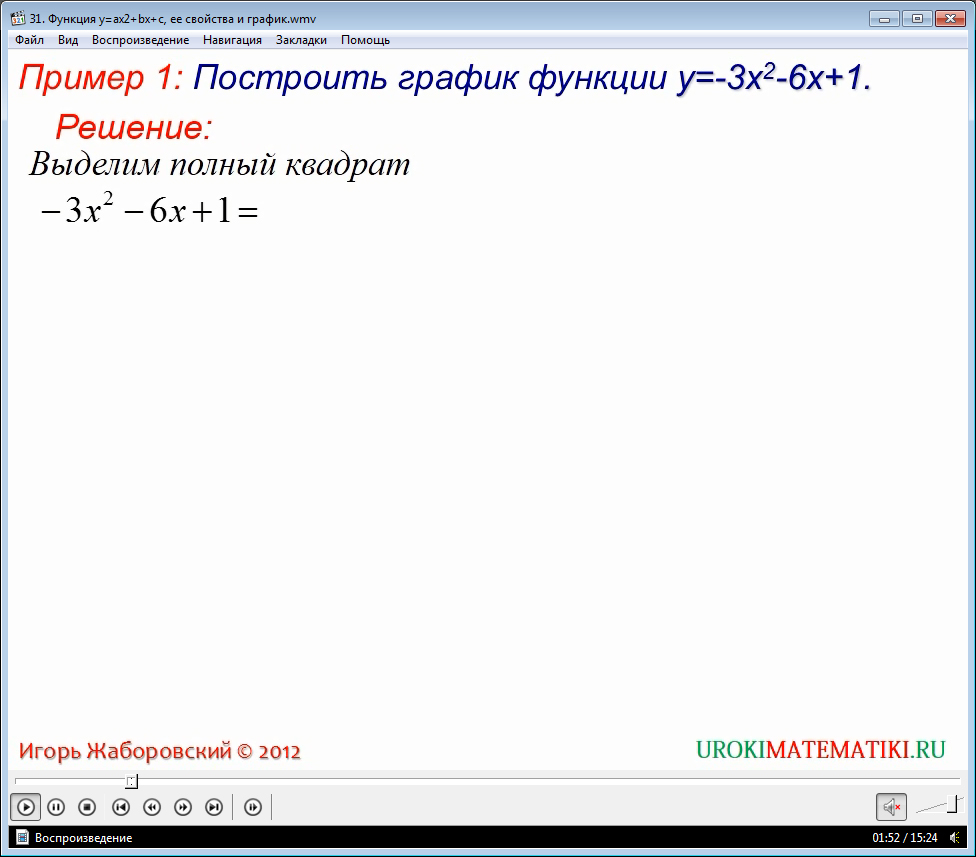
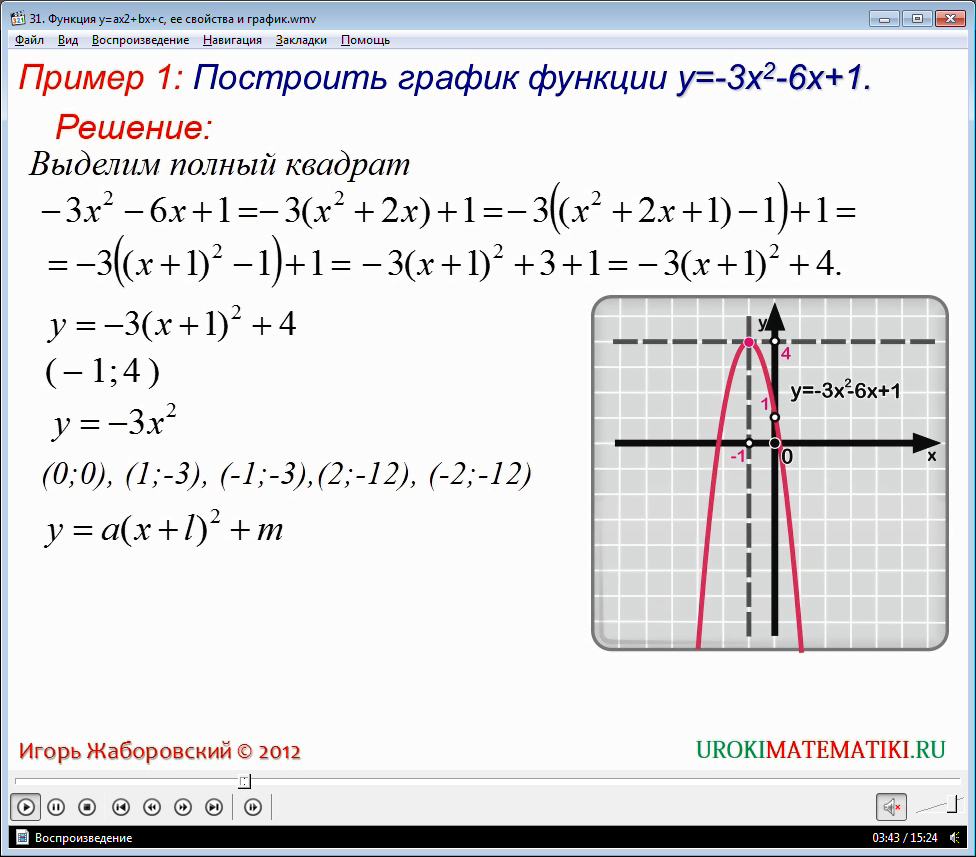
Довольно легко построить график квадратичной функции, например, можно воспользоваться методом выделения полного квадрата.
Построим график полученной функции, перейдя к вспомогательной системе координат с началом в точке с координатами (-1; 4).
Применяя метод выделения полного квадрата, мы имеем квадратичную функцию вида: у = а*(х+1) 2 + m.
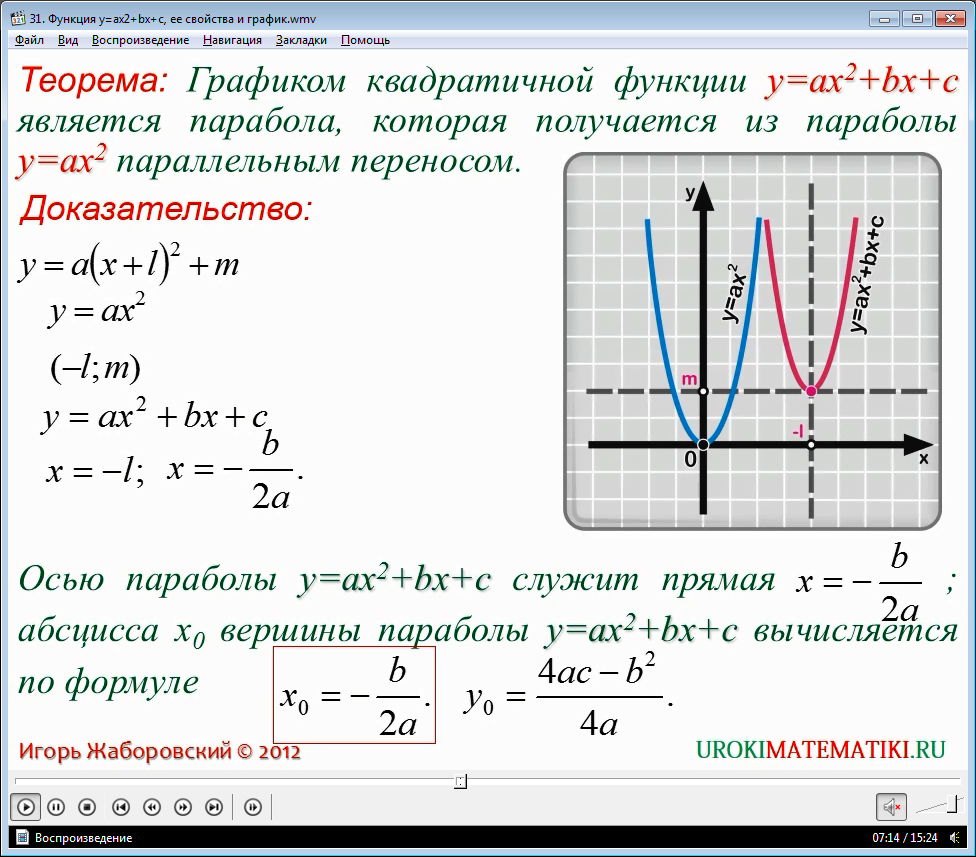
Для определения уравнения оси, направления ее ветвей и координат вершины параболы, рассмотрим следующий пример.
Следующим по сложности идет первый вопрос, потому что требует дополнительных вычислений.
И самый сложный второй, так как, кроме вычислений, еще необходимы знания формул, по которым находятся х нулевое и у нулевое.
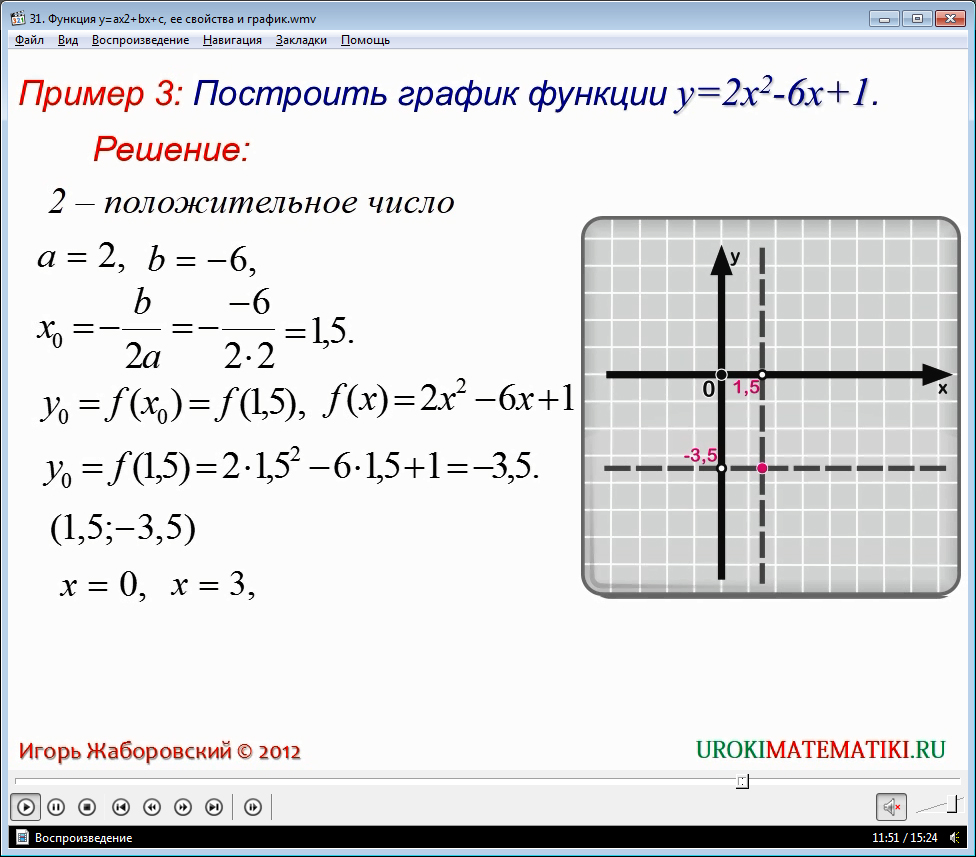
Вершина – (1,5;-3,5). Ось – х=1,5. Возьмем точки х=0 и х=3. у=1. Отметим данные точки. По трем известным точкам строим искомый график.
Для построения графика функции ах 2 + bx + c необходимо:
— найти координаты вершины параболы и отметить их на рисунке, потом провести ось параболы;
— на оси ох взять две симметричные, относительно оси, параболы точки, найти значение функции в этих точках и отметить их на координатной плоскости;
— через три точки построить параболу, при необходимости можно взять еще несколько точек и строить график по ним.
По алгоритму: а=-2, в=8, значит х нулевое равно 2, а у нулевое – 3, (2;3) – вершина параболы, а х=2 является осью.
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Алгоритм нахождения значения коэффициентов a,b, c квадратичной функции
1) По графику параболы определяем координаты вершины ( m;n ).
2) По графику параболы определяем координаты любой точки А ( х 1; у 1 ).
3) Подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
4) Решая полученное уравнение, находим а.
Сначала находим значение коэффициента a (шаг I, смотри выше).
III. нахождение коэффициента с :
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
1) По графику параболы определяем координаты вершины (m;n).
2) По графику параболы определяем координаты любой точки А (х1;у1).
3) Подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
4) Решая полученное уравнение, находим а.
1) Сначала находим значение коэффициента a (шаг I, смотри выше).
2) Вычисляем значение коэффициента b.
III. нахождение коэффициента с:
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a, b).
Номер материала: 371015
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Бельгийский город будет платить детям виртуальные деньги за отказ от неэкологичного транспорта
Время чтения: 0 минут
Только каждый 10-й россиянин может дать платное образование своим детям
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Школьники из России выиграли 8 медалей на Международном турнире по информатике
Время чтения: 3 минуты
Учителя Кубани смогут получить миллион рублей на взнос по ипотеке
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Как определить a, b и c по графику параболы
Предположим, вам попался график функции \(y=ax^2+bx+c\) и нужно по этому графику определить коэффициенты \(a\), \(b\) и \(c\). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью \(y\) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент \(a\) можно найти с помощью следующих фактов:
— Если \(a>0\), то ветви параболы направленных вверх, если \(a 1\), то график вытянут вверх в \(a\) раз по сравнению с «базовым» графиком (у которого \(a=1\)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: \(y=ax^2+bx+c\). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим \(9a\) вместо \(b\):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки \(A\) и \(B\) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение \(a\):
Получается квадратичная функция: \(y=-x^2-9x-15\).
Сразу заметим, что по графику можно сразу определить, что \(c=4\). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: \(C(-1;8)\), \(D(1;2)\) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Сам способ базируется на следующих идеях:
График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).
– Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
— График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц.
График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).
То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:
Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).
Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).
Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).
Разработка урока по алгебре «Функция у=ах^2+вх+с и её свойства»(урок 1)
Выбранный для просмотра документ Конспект урока.docx
муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа №45
Разработка урока по теме
«Функция и её свойства»,
Автор учитель математики
МАОУ СОШ №45 г. Калининграда
Гавинская Елена Вячеславовна.
2016 – 2017 учебный год
Автор – Гавинская Елена Вячеславовна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45
Предмет – математика (модуль «Алгебра»)
Тема – « Функция у = а и её свойства »
Продолжить исследование функции у = ; научить учащихся выполнять преобразования графика квадратичной функции; рассмотреть способы нахождения координат вершин параболы, построения оси симметрии и определения направленности ветвей параболы; подготовить учащихся к введению понятий наибольшего и наименьшего значений квадратного трехчлена.
формирование функциональных представлений на наглядном материале;
формирование умений построения графиков функции у = ;
формирование навыков чтения графиков, умения отражать свойства функции на графике;
формирование способности анализировать, обобщать полученные знания;
развитие навыков применения компьютерных технологий;
формирование логического мышления;
активизировать интерес к получению новых знаний,
воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.
Обоснование выбора методов, средств и форм обучения:
оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
Оборудование и материалы для урока : проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.
Тип урока : комбинированный.
Целесообразность использования медиа продукта на занятии продиктована следующими факторами:
интенсификацией учебно-воспитательного процесса:
автоматизацией процесса контроля,
улучшением наглядности изучаемого материала,
увеличением количества предлагаемой информации,
уменьшением времени подачи материала;
повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.
Обоснование выбора форм и методов работы на обобщающем уроке по теме «Функция у = и её свойства» и методические рекомендации по применению презентации на уроке.
И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.
Объявляется цель и план урока.
Записывается домашнее задание: №602 (2), 617 (проверку этого задания на следующем уроке можно провести с помощью слайдов №14, 15, 16 ).
2.Актуализация опорных знаний.
Учащимся группы А предлагается выполнить самостоятельно задания №8, 9, 10 из Рабочей тетради (стр.101 – 102). При необходимости они пользуются помощью преподавателя. Остальные учащиеся (группы В и С) выполняют на компьютерах тест в Excel «Преобразования графика квадратичной функции». Затем они подсаживаются к ребятам из группы А и в парах проверяют задания из Рабочей тетради. Окончательно – фронтальная проверка с обсуждением трудностей, с которыми столкнулись учащиеся. Последний этап – учащиеся группы А подсаживаются к компьютерам и ребята групп В и С объясняют задания из теста, который они выполняли.
3.Изложение нового материала.
2) Устно учащимся предлагается придумать свои формулы квадратичной функции, а другие ребята называют в предложенных формулах коэффициенты а, в, с.
3) Задаётся провокационный вопрос: будут ли являться квадратичными функции вида у = , у = , у = . После ответа на вопрос учащиеся называют коэффициенты в указанных формулах.
5) Устно фронтально выполняется задание №608.
6) Далее изучение нового материала осуществляется с помощью беседы (с записями в тетрадь) по слайдам №5, 6, 7 .
4. Гимнастика для глаз.
5. Закрепление первичных знаний.
6.Самостоятельная работа обучающего характера.
Учащиеся по вариантам выполняют тест Word «Преобразования графика квадратичной функции». Тетради сдаются на проверку учителю.
7.Подведение итогов урока, выставление отметок.
Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?
Анкетирование можно провести с помощью системы Verdict:
Выставить отметки за работу на уроке.
Выбранный для просмотра документ Опорный конспект.doc