Арккосинус 60 чему равен
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Таблица Брадиса: арккосинус
Вы будете перенаправлены на Автор24
Таблица Брадиса — это таблица, позволяющая высчитывать значения арктангенсов и других тригонометрических функций с высокой точностью.
Для того чтобы воспользоваться таблицей Брадиса, ищут угол в градусах в крайнем столбце слева для синуса (для косинуса в соответствующем столбце справа), а затем в верхней строке минуты. На пересечении строки со столбцом находится искомое значение.
При необходимости найти значения обратных тригонометрических функций — таблицу Брадиса используют наоборот. Например, ищут числовое значение в таблице арктангенсов и тангенсов и для него определяют, в какой строке градусов и столбце минут оно находится.
Таким образом, Таблицу Брадиса можно использовать не только для поиска обычных тригонометрических функций, но и как таблицу арккосинуса и арксинуса, арктангенсов и арккотангенсов.
Сверху в этой статье расположена таблица значений arcsin и arccos, ближе к концу — таблица значений arctg и arcctg.
Таблица Брадиса: таблица arcsin, arccos, cos и sin
Рисунок 1. Таблица Брадиса таблица значений arcsin и arccos. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Таблица. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Таблица значений арктангенсов и арккотангенсов, тангенсов и котангенсов
Рисунок 4. Таблица Брадиса: таблица значений арктангенсов arctg и арккотангенсов arctg. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 7. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Таблица. Автор24 — интернет-биржа студенческих работ
Arcsin arccos arctg arctg таблица значений
Арксинус, arcsin
Определение и обозначения
Арксинус иногда обозначают так:
.
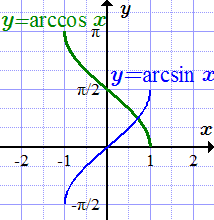
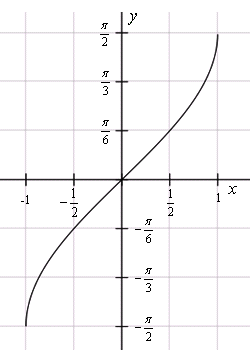
График функции арксинус
Арккосинус, arccos
Определение и обозначения
Арккосинус иногда обозначают так:
.
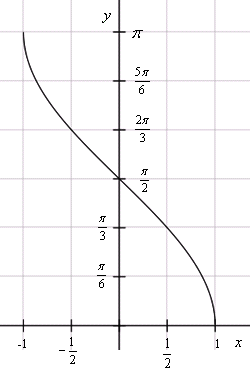
График функции арккосинус
Четность
Функция арксинус является нечетной:
arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0° | 90° | |||
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° |
Формулы
Формулы суммы и разности
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса».
Для этого обратимся к определениям арксинуса, арккосинуса, арктангенса и арккотангенса числа. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать угол, то значением арксинуса, арккосинуса, арктангенса и арккотангенса числа a логично считать величину этого угла. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать число, то оно и является значением соответствующей аркфункции.
Чтобы окончательно все стало понятно, приведем пример.
Основные значения arcsin, arccos, arctg и arcctg
Из таблицы синусов основных углов мы можем извлечь следующие результаты:
Для удобства запишем основные значения арксинуса в таблицу. Основные значения арксинуса (как и приведенные ниже значения арккосинуса, арктангенса и арккотангенса) желательно выучить наизусть, так как с ними придется часто встречаться при решении примеров и задач.
Чтобы получить основные значения арккосинуса, обратимся к таблице косинусов основных углов. Из нее находим, что
Отсюда получаем такие значения арккосинуса:
Вот соответствующая таблица арккосинусов.
Аналогично находятся основные значения арктангенса и арккотангенса. Также занесем их в таблицы арктангенсов и арккотангенсов.
Нахождение значений arcsin, arccos, arctg и arcctg по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Задача нахождения значения арксинуса числа через известный арккосинус этого числа, арккосинуса через известный арксинус, арктангенса через арккотангенс и арккотангенса через известный арктангенс решается очень просто – достаточно использовать формулы arcsin a+arccos a=π/2 и arctg a+arcctg a=π/2 (смотрите формулы суммы арксинуса и арккосинуса, суммы арктангенса и арккотангенса).
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg.
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 1 2 | 2 2 | 3 2 | |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | π 6 | π 4 | π 3 | |
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | π 6 | π 4 | π 3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса».
Для этого обратимся к определениям арксинуса, арккосинуса, арктангенса и арккотангенса числа. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать угол, то значением арксинуса, арккосинуса, арктангенса и арккотангенса числа a логично считать величину этого угла. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать число, то оно и является значением соответствующей аркфункции.
Чтобы окончательно все стало понятно, приведем пример.
Основные значения arcsin, arccos, arctg и arcctg
Из таблицы синусов основных углов мы можем извлечь следующие результаты:
Для удобства запишем основные значения арксинуса в таблицу. Основные значения арксинуса (как и приведенные ниже значения арккосинуса, арктангенса и арккотангенса) желательно выучить наизусть, так как с ними придется часто встречаться при решении примеров и задач.
Чтобы получить основные значения арккосинуса, обратимся к таблице косинусов основных углов. Из нее находим, что
Отсюда получаем такие значения арккосинуса:
Вот соответствующая таблица арккосинусов.
Аналогично находятся основные значения арктангенса и арккотангенса. Также занесем их в таблицы арктангенсов и арккотангенсов.

Нахождение значений arcsin, arccos, arctg и arcctg по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Задача нахождения значения арксинуса числа через известный арккосинус этого числа, арккосинуса через известный арксинус, арктангенса через арккотангенс и арккотангенса через известный арктангенс решается очень просто – достаточно использовать формулы arcsin a+arccos a=π/2 и arctg a+arcctg a=π/2 (смотрите формулы суммы арксинуса и арккосинуса, суммы арктангенса и арккотангенса).
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg.
Тригонометрия. Обратные тригонометрические функции. Арккосинус.
Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям.
Арккосинус, обратная функция к cos (x = cos y), y = arccos x определен при 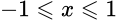
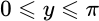
Арккосинус (обозначение: arccos x; arccos x — это угол, косинус которого равняется x и так далее).
Функция y = cos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей.
Дана функция y = cos x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — [0; π]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0; π] существует обратная функция y = arccos x, график которой симметричен графику y = cos x на отрезке [0; π] относительно прямой y = x.