Асимптота что это такое простыми словами

Асимптоты графика функции

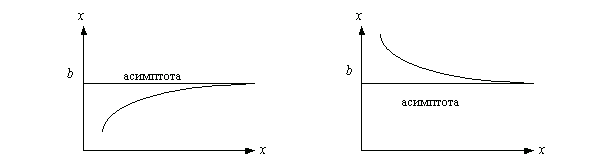
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.

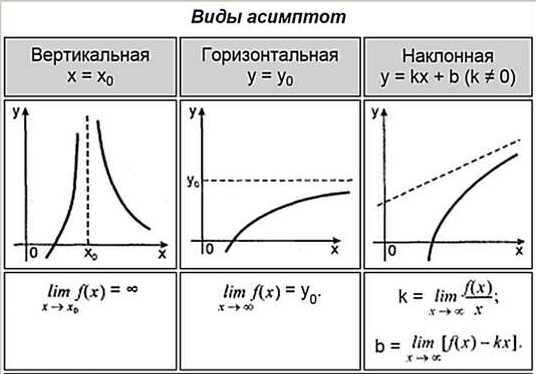
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.

Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три. и бесконечно много. У каждой функции по разному.

Вертикальные асимптоты

Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.

Горизонтальные асимптоты

Наклонные асимптоты

Примеры решений

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Приступим к поиску наклонных асимптот.

Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты.

Нет точек разрыва, а это значит, нет вертикальных асимптот.

Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.

Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.

Источник

Асимптота

Полезное

Смотреть что такое «Асимптота» в других словарях:

АСИМПТОТА — (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка

АСИМПТОТА — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия

АСИМПТОТА — (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь

асимптота — Прямая линия, к которой постепенно приближается кривая. [http://www.morepc.ru/dict/] асимптота Прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или … Справочник технического переводчика

Асимптота — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь

АСИМПТОТА — жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля

асимптота — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Асимптота — (от греч. слов: a, sun, piptw) несовпадающая. Подасимптотой подразумевается такая линия, которая, будучи неопределеннопродолжена, приближается к данной кривой линии или к некоторой ее частитак, что расстояние между общими линиями делается менее… … Энциклопедия Брокгауза и Ефрона

Асимптота — поверхности называется прямая линия, пересекающаяповерхность по крайней мере в двух бесконечно удаленных точках … Энциклопедия Брокгауза и Ефрона

АСИМПТОТА — (asymptote) Значение, к которому стремится данная функция при изменении аргумента (argument), но не достигает его ни при одном конечном значении аргумента. Например, если общая стоимость выпуска х задается функцией ТС=а+bх, где а и b – константы … Экономический словарь

Асимптота — [asymptote] прямая, к которой стремится (никогда не достигая ее), имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или уменьшается. Например, в функции: y = c + 1/x значение y приближается с… … Экономико-математический словарь

Источник

Асимптота

Смотреть что такое «Асимптота» в других словарях:

АСИМПТОТА — (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка

АСИМПТОТА — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия

АСИМПТОТА — (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь

асимптота — Прямая линия, к которой постепенно приближается кривая. [http://www.morepc.ru/dict/] асимптота Прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или … Справочник технического переводчика

Асимптота — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь

АСИМПТОТА — жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля

асимптота — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Асимптота — (от греч. слов: a, sun, piptw) несовпадающая. Подасимптотой подразумевается такая линия, которая, будучи неопределеннопродолжена, приближается к данной кривой линии или к некоторой ее частитак, что расстояние между общими линиями делается менее… … Энциклопедия Брокгауза и Ефрона

Асимптота — поверхности называется прямая линия, пересекающаяповерхность по крайней мере в двух бесконечно удаленных точках … Энциклопедия Брокгауза и Ефрона

АСИМПТОТА — (asymptote) Значение, к которому стремится данная функция при изменении аргумента (argument), но не достигает его ни при одном конечном значении аргумента. Например, если общая стоимость выпуска х задается функцией ТС=а+bх, где а и b – константы … Экономический словарь

Асимптота — [asymptote] прямая, к которой стремится (никогда не достигая ее), имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или уменьшается. Например, в функции: y = c + 1/x значение y приближается с… … Экономико-математический словарь

Источник

Асимптота

Полезное

Смотреть что такое «Асимптота» в других словарях:

АСИМПТОТА — (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка

АСИМПТОТА — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия

АСИМПТОТА — (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь

асимптота — Прямая линия, к которой постепенно приближается кривая. [http://www.morepc.ru/dict/] асимптота Прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или … Справочник технического переводчика

Асимптота — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь

АСИМПТОТА — жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля

асимптота — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Асимптота — поверхности называется прямая линия, пересекающаяповерхность по крайней мере в двух бесконечно удаленных точках … Энциклопедия Брокгауза и Ефрона

АСИМПТОТА — (asymptote) Значение, к которому стремится данная функция при изменении аргумента (argument), но не достигает его ни при одном конечном значении аргумента. Например, если общая стоимость выпуска х задается функцией ТС=а+bх, где а и b – константы … Экономический словарь

Асимптота — [asymptote] прямая, к которой стремится (никогда не достигая ее), имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или уменьшается. Например, в функции: y = c + 1/x значение y приближается с… … Экономико-математический словарь

Источник

Асимптота графика функции: определение, как искать

Что такое асимптота — понятие и определение

Асимптота графика функции у=f (x) представляет собой прямую L, максимально приближающеюся к графику функции, точка которого стремится к бесконечности, то есть неограниченно удаляется от начала координат по кривой. Расстояние между этой точкой функции у=f(x) и асимптотой L стремится к нулю.

На рисунке приведены примеры асимптот графиков функций.

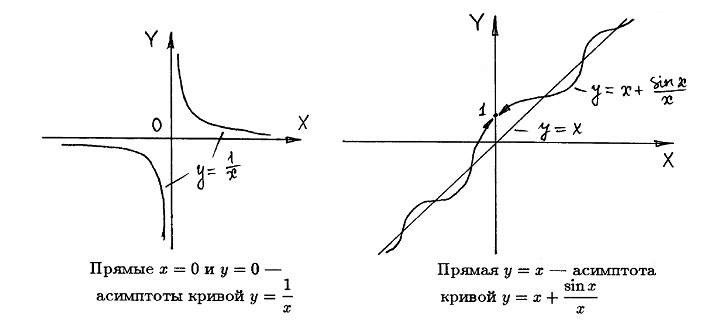
На рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон

Асимптоты графика функции, основные виды

Асимптоты делятся на три вида: вертикальные, наклонные и горизонтальные.

У разных функции в наличии может быть различное количество асимптот:

Приведем пример нахождения асимптот гиперболы.

Гипербола — геометрическое место расположения точек, от которых абсолютная величина разности растояний до двух фокусов (заданных точек), является постоянной и меньшей, чем расстояние между самими фокусами.

Это действительно, так как:

Следовательно, если абсцисса х неограниченно возрастает, то график гиперболы и ее асимптота неограниченно сближаются.

Расположение асимптот гиперболы соответствует диагоналям прямоугольника, стороны которого параллельны оси Ох и оси Оу, а центром служит начало координат.

Пример

Необходимо составить уравнение гиперболы, если следующие уравнения задают ее асимптоты:

Решение

Применим формулу \(y=\frac bax\) и получим:

Подставим координаты точки М в общую формулу уравнения гиперболы:

Получим систему уравнений. Чтобы получить уравнение данной гиперболы, необходимо вычислить полученную систему уравнений.

Вертикальные асимптоты

Если хотя бы один из пределов \(\lim_f(x)\) или \(\lim_f(x)\) является равным +∞ или —∞, то вертикальной асимптотой графика функции у=f(x) будет являться прямая х=с.

Примеры вертикальных асимптот:

Пример 1

Необходимо определить вертикальную асимптоту функции \(\lim_a(x)=0.\)

Решение

то x=0 — вертикальная асимптота.

Пример 2

Ось ординат является вертикальной асимптотой, так как

Наклонные асимптоты

Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.

Если k=0, то наклонная асимптота превращается в горизонтальную.

Применение правила Лопиталя

Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:

Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:

Производная может применяться многократно для получения константы в числителе или знаменателе.

Пример 1

Прямая у=х — наклонная асимптота графика данной функции.

Пример 2

Рассмотрим два варианта:

То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.

То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.

Горизонтальные асимптоты

Прямая y=b является горизонтальной асимптотой для графика функции y=f(x), если

Пример 1

Имеется функция: \(y=4+\frac1x.\)

поэтому y=4 — горизонтальная асимптота данной функции.

Пример 2

Значит, у=1 — горизонтальная асимптота графика функции.

Пример 3

Источник