Аттрактор что это такое
Значение слова «аттрактор»
Существуют различные формализации понятия стремления, что приводит к различным определениям аттрактора, задающим, соответственно, потенциально различные множества (зачастую — вложенные одно в другое). Наиболее употребительными определениями являются максимальный аттрактор (зачастую — в своей малой окрестности, см. ниже), аттрактор Милнора и неблуждающее множество.
Аттракторы классифицируют по:
Формализации понятия стремления: различают максимальный аттрактор, неблуждающее множество, аттрактор Милнора, центр Биркгофа, статистический и минимальный аттрактор.
Регулярности самого аттрактора: аттракторы делят на регулярные (притягивающая неподвижная точка, притягивающая периодическая траектория, многообразие) и странные (нерегулярные — зачастую фрактальные и/или в каком-либо сечении устроенные как канторово множество; динамика на них обычно хаотична).
Локальности («притягивающее множество») и глобальности (здесь же — термин «минимальный» в значении «неделимый»).
Также, есть известные «именные» примеры аттракторов: Лоренца, Плыкина, соленоид Смейла-Вильямса, гетероклинический аттрактор (пример Боуэна).
аттра́ктор
1. физ. состояние динамической системы, к которому она стремится с течением времени ◆ Точки, притягивающие траекторию развивающейся динамической системы, получили название аттракторов (от английского attract ― привлекать, притягивать). Владимир Горбачев, «Концепции современного естествознания», 2003 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова печище (существительное):
Аттрактор
Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).
Существуют различные формализации понятия стремления, что приводит к различным определениям аттрактора, задающим, соответственно, потенциально различные множества (зачастую — вложенные одно в другое). Наиболее употребительными определениями являются максимальный аттрактор (зачастую — в своей малой окрестности, см. ниже), аттрактор Милнора и неблуждающее множество.
Аттракторы классифицируют по:
Также, есть известные «именные» примеры аттракторов: Лоренца, Плыкина, соленоид Смейла-Вильямса, гетероклинический аттрактор (пример Боуэна).
Содержание
Свойства и связанные определения
При всех определениях аттрактор полагается замкнутым и (полностью) инвариантным множеством.
С понятием аттрактора также тесно связано понятие меры Синая-Рюэлля-Боуэна: инвариантной меры на нём, к которой стремятся временные средние типичной (в смысле меры Лебега) начальной точки либо временные средние итераций меры Лебега. Впрочем, такая мера существует не всегда (что иллюстрирует, в частности, пример Боуэна).
Виды формализации определения
Поскольку всё фазовое пространство в любом случае сохраняется динамикой, формальное определение аттрактора можно давать, исходя из философии, что «аттрактор это наименьшее множество, к которому всё стремится» — иными словами, выкидывая из фазового пространства всё, что может быть выкинуто.
Максимальный аттрактор
Пусть для динамической системы задана область 
, которая переводится строго внутрь себя динамикой:
Тогда, максимальным аттрактором системы в ограничении на U называется пересечение всех его образов под действием динамики:
То же самое определение можно применить и для потоков: в этом случае, необходимо потребовать, чтобы векторное поле, задающее поток, на границе области было направлено строго внутрь неё.
У этого определения есть два недостатка. Во-первых, для его применения необходимо найти поглощающую область. Во-вторых, если такая область была выбрана неудачно — скажем, содержала отталкивающую неподвижную точку с её бассейном отталкивания — то в максимальном аттракторе будут «лишние» точки, около которых на самом деле несколько раз подряд оказаться нельзя, но текущий выбор области этого «не чувствует».
Аттрактор Милнора
По определению, аттрактором Милнора динамической системы называется наименьшее по включению замкнутое множество, содержащее ω-предельные множества почти всех начальных точек по мере Лебега. Иными словами — это наименьшее множество, к которому стремится траектория типичной начальной точки.
Неблуждающее множество
Точка x динамической системы называется блуждающей, если итерации некоторой её окрестности U никогда эту окрестность не пересекают:
0 \quad f^n(U)\bigcap U =\emptyset. » border=»0″ />
Иными словами, точка блуждающая, если у неё есть окрестность, которую любая траектория может пересечь только один раз. Множество всех точек, не являющихся блуждающими, называется неблуждающим множеством.
Статистический аттрактор
Статистический аттрактор определяется как наименьшее по включению замкнутое множество 
, в окрестности которого почти все точки проводят почти всё время: для любой его окрестности для почти любой (в смысле меры Лебега) точки 
выполнено
Минимальный аттрактор
Минимальный аттрактор определяется как наименьшее по включению замкнутое множество 
, в окрестности которого почти вся мера Лебега проводит почти всё время: для любой его окрестности выполнено
Примеры несовпадений
Локальность, минимальность и глобальность
Регулярные и странные аттракторы
Регулярные аттракторы
Притягивающая неподвижная точка
(пример: маятник с трением)
Предельный цикл
(пример: микрофон+колонки, осциллятор Ван дер Поля)
Странные аттракторы
(примеры: аттрактор Лоренца, аттрактор Рёсслера, соленоид Смейла-Вильямса; комментарий про эффект бабочки и про динамический хаос.)
Странный аттрактор — это аттрактор, имеющий два существенных отличия от обычного аттрактора: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима нарастают). Основным критерием хаотичности аттрактора является экспоненциальное нарастание во времени малых возмущений. Следствием этого является «перемешивание» в системе, непериодичность во времени любой из координат системы, сплошной спектр мощности и убывающая во времени автокорреляционная функция.
Динамика на странных аттракторах часто бывает хаотической: прогнозирование траектории, попавшей в аттрактор, затруднено, поскольку малая неточность в начальных данных через некоторое время может привести к сильному расхождению прогноза с реальной траекторией. Непредсказуемость траектории в детерминированных динамических системах называют динамическим хаосом, отличая его от стохастического хаоса, возникающего в стохастических динамических системах. Это явление также называют эффектом бабочки, подразумевая возможность преобразования слабых турбулентных потоков воздуха, вызванных взмахом крыльев бабочки в одной точке планеты в мощное торнадо на другой её стороне вследствие многократного их усиления в атмосфере за некоторое время.
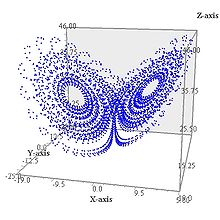
Среди странных аттракторов встречаются такие, хаусдорфова размерность которых отлична от топологической размерности и является дробной. Одним из наиболее известных среди подобных аттракторов является аттрактор Лоренца.
Именные примеры
Аттрактор Лоренца
Система диф. уравнений, создающих аттрактор Лоренца имеет вид:
при следующих значениях параметров: 
, 
, 
. Аттрактор Лоренца не является классическим, и даже не является странным в смысле Смейла. [2]
Соленоид Смейла-Вильямса
Соленоид Смейла-Вильямса — пример обратимой динамической системы, аналогичной по поведению траекторий отображению удвоения на окружности. Более точно, эта динамическая система определена на полнотории, и за одну её итерацию угловая координата удваивается; откуда автоматически возникает экспоненциальное разбегание траекторий и хаотичность динамики. Также соленоидом называют и максимальный аттрактор этой системы (откуда, собственно, и происходит название): он устроен как (несчётное) объединение «нитей», наматывающихся вдоль полнотория.
Аттрактор Плыкина
Пример Боуэна, или гетероклинический аттрактор
Аттрактор Эно
Гипотезы
Гипотеза Палиса
Гипотезы Рюэля
См. также
Примечания
Ссылки и литература
Полезное
Смотреть что такое «Аттрактор» в других словарях:
аттрактор — точка притяжения Словарь русских синонимов … Словарь синонимов
АТТРАКТОР — см. Синергетика. Большой психологический словарь. М.: Прайм ЕВРОЗНАК. Под ред. Б.Г. Мещерякова, акад. В.П. Зинченко. 2003 … Большая психологическая энциклопедия
Аттрактор — потенциальное состояние системы, к которому она эволюционирует. По Князевой: конечная область неминуемого схождения фазовых траекторий движения сложной системы. В качестве аттрактора может выступать или точка (устойчивый фокус), или иное более… … Словарь-справочник по философии для студентов лечебного, педиатрического и стоматологического факультетов
аттрактор — 3.1.1 аттрактор: Фактор саморазвития системы, влияющий на ее самоорганизацию и способность к взаимосодействию ее основных частей. Источник … Словарь-справочник терминов нормативно-технической документации
Аттрактор — (от лат. attraho притягиваю к себе) некоторая область, к которой притягиваются (сходятся) все возможные траектории движения систем … Начала современного естествознания
аттрактор — Syn: точка притяжения … Тезаурус русской деловой лексики
АТТРАКТОР — структура (функция), задающая (определяющая) устойчивое состояние любой системы. (См. синергетика, нелинейное мышление) … Философия науки: Словарь основных терминов
Аттрактор — (лат. притягиваю к себе) точка или множество точек (замкнутая кривая), к которому стремятся параметры состояния диссипативной системы, конечное состояние диссипативной системы (см. Система диссипативная) … Концепции современного естествознания. Словарь основных терминов
Аттрактор Рёсслера — Аттрактор Рёсслера хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера … Википедия
Аттрактор Плыкина — пример динамической системы на диске, максимальный аттрактор которой гиперболичен. В частности, этот пример структурно устойчив, как удовлетворяющий аксиоме A Смейла. Конструкция Аттрактор Плыкина строится как фактор диффеоморфизма тора,… … Википедия
Визуализация хаоса: как представляют аттракторы динамических систем
(с)
Среди ученых ходит байка о нетривиальном способе сделать свой доклад интересным и увлекательным. Во время выступления нужно выбрать в зале самого недоумевающего, самого потерянного слушателя, и рассказывать персонально ему, да так, чтобы зажечь в глазах огонек интереса.
Еще известен афоризм, приписываемый физику Ричарду Фейнману: «Если вы ученый, квантовый физик, и не можете в двух словах объяснить пятилетнему ребенку, чем вы занимаетесь, — вы шарлатан».
Доступно объяснять устройство сложных вещей — великий навык, однако бывают истории, о которые сломает язык даже самый искусный оратор. Теория динамических систем – вот та область, где без визуализации чувствуешь себя слепым садовником в окружении колючих, увенчанных шипами растений.
Сложные непериодические режимы поведения динамических систем можно описать непериодическими траекториями — так называемыми странными аттракторами, имеющими фрактальную структуру. Сегодня покажем, как визуализируют поведение странных и некоторых других аттракторов.
Great attractor
Если остановить на улице первого попавшегося человека, посветить ему в лицо фонариком и спросить, что он знает об аттракторах, то, скорее всего, ничего не услышим услышим о Великом аттракторе, притягивающем к себе в глубинах космоса сотни тысяч галактик, чтобы однажды перезапустить Матрицу.
На самом деле космологические аттракторы — это области гравитационной аномалии, вызванные, по всей видимости, особыми галактическими скоплениями, и не имеющие прямого отношения к теме статьи.
Безусловно, стоит отметить, что теория динамических систем особенно хорошо подходит для определения возможных асимптотических состояний различных космологических моделей. Да и видео интересное — посмотрите.
Lorenz attractor
Один из самых знаменитых аттракторов — аттрактор Лоренца, получивший известность благодаря массовому распространению термина «эффект бабочки». Помимо того, что при визуализации аттрактора его форма напоминает бабочку, он представляет собой набор хаотических решений системы Лоренца.
Демонстрация хаотических систем, подобных аттрактору Лоренца (можно сделать самому на C++).
Суть решений Эдварда Лоренца в нелинейной системе обыкновенных дифференциальных уравнений можно передать следующим образом: в любой физической системе при отсутствии совершенного знания начальных условий мы не способны в полной мере предсказать ее будущее. Физические системы могут быть полностью непредсказуемыми даже при отсутствии квантовых эффектов.
Hidden attractor
Аттрактор называется скрытым, если его область притяжения не пересекается с определенной открытой окрестностью точек равновесия. В противном случае он называется самовозбуждающимся аттрактором (self-excited attractor).
Классификация аттракторов (скрытые или самовозбуждающиеся) появилась только в 2009 году — после того как был обнаружен скрытый аттрактор в простейшей электрической цепи Чуа с одним нелинейным резистором, демонстрирующей режимы хаотических колебаний.
Multiscroll attractor
Это целое семейство многокомпонентных аттракторов, включающее в том числе модифицированный скрытый хаотический аттрактор Чуа.
Nonchaotic attractor
Помимо «обычных» хаотических аттракторов существуют периодические, квазипериодические, а также странные нехаотические аттракторы.
Один из основных критериев, по которому аттрактор можно причислить к нехаотическим, — расчет показателей Ляпунова. В этом типе аттракторов для системы экспоненты Ляпунова не являются положительными.
Hyperchaotic attractor
Hyperchaotic attractor — это визуализация дифференциальных уравнений Safieddine Bouali. Гиперхаотические аттракторы существуют только в динамических системах, размерность фазового пространства которых более или равна четырем. Модели гиперхаотических аттракторов могут использоваться в реальных приложениях, имеющих отношение к безопасной связи и шифрованию.
Limit Cycle
Непрерывная динамическая система с изолированной орбитой, подразумевающая самоподдерживающиеся колебания (например, колебания маятниковых часов или сердцебиение во время отдыха).
Rössler attractor
Хаотический аттрактор системы дифференциальных уравнений Рёсслера. В 1976 году врач Отто Рёсслер представил трехмерную модель динамики химических реакций, протекающих в некоторой смеси с перемешиванием. Для аттрактора Рёсслера характерна фрактальная структура в фазовой плоскости.
На аттракторе Рёсслера траектории не пересекают сами себя. Поверхности, образующие странный аттрактор, делятся на отдельные слои, создавая бесконечное множество поверхностей, каждая из которых находится чрезвычайно близко к соседней. Можно допустить, что лента, которая образует основание аттрактора, подобна многослойному листу Мёбиуса.
Spiral attractor
Spiral attractor — аттрактор, позволивший изучить жизнь амеб Dictyostelium discoideum. При истощении питательных ресурсов амебы секретируют циклический аденозинмонофосфат (цАМФ) — сигнальные молекулы, привлекающие соседние клетки к центральному местоположению. Голодные миксамёбы (одноклеточная стадия развития Dictyostelium), подчиняясь сигналам, сползаются к центру, который образовался в результате «склеивания» первых миксамёб, случайно оказавшихся рядом. Соединяясь с помощью молекул клеточной адгезии, они образуют агрегат из нескольких десятков тысяч клеток. Собственно, этот процесс и представлен на видео.
Tinkerbell attractor
Карта Тинкербелла — динамическая система с дискретным временем, демонстрирующая хаотическое поведение в двумерном пространстве. Форму Тинкербелла можно изменить, чтобы получить другие хаотические аттракторы в системах защищенных коммуникаций, использующих хаос связи.
Thomas’ cyclically symmetric attractor
Трехмерный аттрактор, предложенный биоинформатиком Рене Томасом, может рассматриваться как траектория демпфирующей частицы, движущейся в трехмерной решетке сил.
Ikeda attractor
Фрактальный набор, к которому притягивается орбита любой точки на плоскости, если мы продолжаем итерацию определенной карты от плоскости к самой себе.
Заключение
Мы рассмотрели лишь несколько известных типов аттракторов. Всего же вы можете найти упоминания о сотне различных аттракторов.
Надо отметить, что это очень молодая область науки, и поиск, начавшийся с идеи уйти от математической абстракции в сторону практического «создания» хаоса, продолжается по сей день.
Неизменно одно: наш интерес с силой Великого аттрактора притягивают системы, чрезвычайно чувствительные к небольшим отклонениям в описании начального состояния. Мы сталкиваемся с этими системами не из праздного любопытства — мы живем среди них и благодаря им.
Курс на Великий Аттрактор
Уважаемые читатели, в своей скромной статье я хочу рассказать о таком астрономическом понятии как «Великий аттрактор» (Великий центр притяжения). Наверняка те из вас кто увлекается астрономией уже знакомы с данной темой, но есть и такие читатели, вроде меня, которые впервые столкнулись с данным понятием.
Ученым давно было известно, что наша галактика движется в направлении созвездия Центавра, но причина движения долго оставалась загадкой. Около 30 лет назад была выдвинута теория, согласно которой Млечный путь испытывает притяжение не только со стороны других объектов местной группы, но и более отдаленного крупного скопления материи с массой более 10 квадриллионов больше массы Солнца, названного Великим Аттрактором.
Местная группа – скопление галактик, в которое входит Млечный путь. Насчитывает более чем 54 галактики с гравитационным центром где-то между Млечным путем и галактикой М31 – Андромеда. Входит в сверхскопление Девы.(Wikipedia)
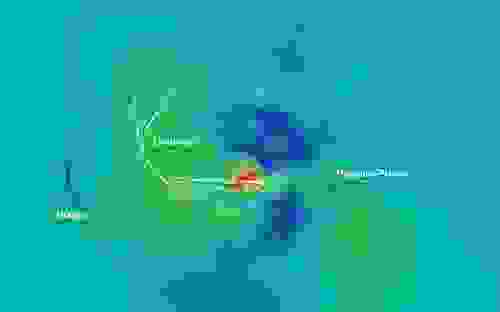
Более внимательно и подробно изучить Великий аттрактор не представлялось возможным из-за его нахождения в «зоне избегания» — области за плоскостью «Млечного пути», где газ и пыль содержащиеся в нашей галактике блокируют видимый свет от объектов за ее пределами.
Решением проблемы послужило исследование кластеров в зоне избегания (CIZA), проводимое учеными Института Астрономии при Гавайском Университете. Для изучения труднодоступных регионов было использовано рентгеновское излучение, которое с легкостью преодолевает облака газа и пыли. Скопления галактик являются источниками рентгеновкого излучения, что облегчает задачу наблюдения.
Зона избегания в настоящее время достаточно хорошо изучена. Галактический газ и пыль хорошо преодолеваются радиоволнами и светом в инфракрасном диапазоне. Самые известные находки за зоной избегания включают галактики Maffei 1 и Maffei 2, Dwingeloo 1 и Dwingeloo 2.
По результатам исследования, в районе предполагаемого расположения «Великого Аттрактора» было обнаружено меньше массивных галактических скоплений чем предполагалось. Тем не менее, гравитационная аномалия около центра Великого аттрактора, скопления Abell 3627, оказалась достаточной силы, чтобы разорвать на части спиральную галактику ESO 137-001 (фото — Hubble) 
Но самое интересное, что Астрономы Гавайского Университета обнаружили еще более массивное скопление галактик на расстоянии более чем 500 миллионов световых лет (5 секстиллионов км.) от «Млечного пути», далеко за «Великим Аттрактором», в районе сверхскопления Шепли.
Сверхскопление Шепли, обнаруженное в 1930г. Харлоу Шепли, является самым массивным сверхскоплением галактик из 220 известных сверхскоплений в обозримой вселенной. Оно содержит массу примерно в 10,000 раз большую чем масса Млечного пути и в 4 раза большую чем масса наблюдаемая в области «Великого Аттрактора».
Так же было проведено исследование, которое позволило рассчитать что вклад в скорость движения местной группы со стороны Великого Аттрактора составляет 44%, остальная часть связана с глобальным течением, где значительная часть локальной вселенной, включая сам «Великий Аттрактор» движется в направлени еще более сильного центра притяжения, в районе суперкластера Шепли. 
Недавно, в Августе 2014г. астрономы построили трехмерную визуализацию сверхскопления Ланиакеа, в которое входит и сверхскопление Девы содержащее наш родной «Млечный Путь». Так вот, всю площадь Ланиакеа можно представить как долину, окруженную горами с которых к самой нижней точке долины стекают реки и ручьи.
«Нижняя точка» представляет из себя новый «Великий Аттрактор» и является сердцем Ланиакеа. 