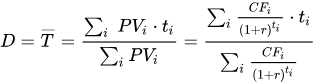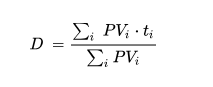дюрация по маколею что это
Очень надеюсь, что эта статья окажется максимально понятной и полезной для сообщества инвесторов, так как сам очень долго понимал смысл дюрации.
Первое, что вам нужно знать, слово дюрация — это адаптация на русский язык слова (duration — длительность). И отсюда же вытекает второй момент. Раз у нас дюрация — это на самом деле длительность, сразу становится логично, что измеряется данный показатель во временных единицах (обычно годы, могут быть дни).
Не смотрите Википедию
Мы все хотим, чтобы нам объясняли так, чтобы было понятно. Когда заходишь на википедию и видишь формулу дюрации — совсем непонятно:
Формула дюрации на википедии
Формулу выше можете не запоминать, важно здесь осознать только первую ее часть:
Упрощенная формула дюрации
Числитель:
Сумма из (поступление по облигации * время поступления)
Знаменятель:
Сумма из поступлений
Возьмем 3 облигации с одинаковой доходностью:
Облигация с номиналом 1000 рублей без купона и выплатой процента в конце срока 1 раз (100 рублей = 10%):
D = 1 год * 1100 рублей (номинал + процент) / 1100 рублей = 1 год.
Облигация с номиналом 1000 рублей с купоном 1 раз в полгода 50 рублей:
D = 0.5 года * 50 рублей + 1 год * 1050 рублей / 1100 рублей = 0,97 года (упрощенно)
Облигация с номиналом 1000 рублей и купоном 1 раз в квартал по 25 рублей
D = 0.25 года * 25 рублей + 0.5 года * 25 рублей + 0.75 года * 25 рублей + 1 год * 1025 рублей / 1100 рублей = 0.96 года (упрощенно)
Имея 3 облигации с одинаковой доходность мы получаем разную дюрацию. Что это значит и какой же вообще смысл данной формулы
Смысл формулы дюрации:
Дюрация показывает среднее время, за которое мы полностью вернем свои вложения в облигации. Таким образом очевидно, что при прочих равных условиях нужно выбирать облигации с меньшей дюрацией, или сроком возврата средств.
Бытовой пример:
Чтобы осознать полезность дюрации — можете представить следующую ситуацию:
К вам пришли 2 друга, оба хотят одолжить 100 000 рублей под 20% в год
Очевидно, что вам больше понравится второй вариант, так как вы свои деньги начнете получать назад уже через месяц. Дюрация во втором случае будет ниже.
Можно провести здесь аналогию с показателем P/E в акциях, который также отражает количество лет, за которые бизнес окупит себя. Как и P/E позволяет удобно сравнивать между собой акции, так и дюрация позволяет удобно сравнивать между собой облигации.
Сложная формула дюрации (из википедии) получается потому, что 100 рублей сейчас НЕ РАВНЫ 100 рублей через 1 год и т.п. Поэтому все поступления должны идти с соотвествующими коэффициентами (должны быть продисконтированы), которые зависят от процентной ставки.
Представьте, что к вам пришли те же 2 друга, но они хотят взять 100 000 рублей не на 1 год, а на 10 лет и под все те же 20% годовых
Дюрация во втором случае опять будет меньше — это понятно. Но на этот раз вероятно вы подумаете, что может быть вообще не стоит давать деньги друзьям, так как экономически ситуация может поменяться так, что если сейчас вы на эти 100 000 рублей можете всей семьей поехать в отпуск, то через 10 лет, кто знает, на эти деньги вы сможете купить разве что продуктов на вечер.
То есть временной фактор очень важен, так как еще раз повторю, 100 рублей сегодня НЕ РАВНЫ 100 рублей через год. Так вот наша сложная формула дюрации (из википедии) на самом деле учитывает и этот фактор, так как все поступления продисконтированы (взяты с коэффициентом) относительно процентной ставки. И поэтому на самом деле дюрация во втором случае будет намного меньше чем в первом, но она будет намного больше, чем когда друзья просили деньги на год.
Из этого вытекает главное, что вам нужно понять
Чем выше дюрация, тем выше неопределенность (риск) для инвестора.
На практике это оказывается очень интересно. Так как стоимость денег, как и сама дюрация, зависят от процентной ставки, собственно, как и тело облигации (а вы ведь знаете, что если ставки растут — облигации падают и наоборот), получается что есть реальная связь между изменением процентной ставки и изменением стоимости облигации в зависимости от дюрации.
Изменение процентной ставки на 1% в любую сторону вызывает изменение стоимости облигации на процент равный дюрации в противоположную сторону.
Пример:
Повысили ставку на 1%
Понизили ставку на 6.5% (так было в России несколько лет назад — правда ставку тогда повысили)
Практическая польза от понимания дюрации следующая:
Если у вас остались вопросы по этой теме — задавайте их в комментариях здесь или в нашем блоге.
Облигации: мифы и реальность. Часть 2. Глава 1. Дюрация Маколея.
В глянцевом журнале для тиньковских домохозяек https://journal.tinkoff.ru/ часто можно встретить такие мнения о дюрации:
“Дюрация — это эффективный срок до погашения облигации”
“С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций”
“Простыми словами — это количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги”
“Дюрация — это средняя окупаемость инвестиции”
При этом читателю вряд ли будет понятно, что в данном случае означают слова “эффективный” и “средний срок возврата”, а авторы таких статей в детали обычно не вдаются. Мы на примерах покажем, что эти дефиниции иногда могут сбить инвестора с толку, а в некоторых случаях бывают неверны. Мы продолжаем считать, что наши облигации живут в мире плоских процентных ставок, но иногда в нем могут происходить скачкообразные изменения кривой бескупонной доходности.
Дюрация Маколея
В вышеприведенных определениях под дюрацией авторы понимают прежде всего дюрацию Маколея, и она действительно была введена исторически как средневзвешенное время денежных потоков от облигации. (F.Macaulay, 1938) Он, собственно, и рассматривал дюрацию как некую оценку “срока жизни” облигации.
Выражение для дюрации Маколея хорошо известно и мы не будем его приводить, а обсудим лишь некоторые конкретные примеры.
Прежде всего обратим внимание, что единица измерения дюрации — временной интервал (годы, дни и т.д) И наилучшим образом понятию “количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги” отвечает дюрация бескупонной облигации, ведь она в точности равна времени до погашения T (в чем легко убедиться, посмотрев на формулу) Конечно же, деньги вернутся с лихвой, обеспечив держателю процент от вложений, но промежуточных выплат по такой облигации нет, и придется дожидаться погашения номинальной стоимости.
Если облигация платит купоны, то ее дюрация всегда меньше времени до погашения, а чем выше размер купона и/или ставка дисконтирования, тем меньше дюрация. Поэтому возникает восприятие дюрации как “эффективного срока до погашения”, ведь какую-то “часть” инвестор получает заранее, и чем раньше, тем для него лучше. Проблема в том, что данная эффективность в сознании инвестора не имеет четких критериев, она никак и никем количественно не определена. Это скорее качественный показатель, позволяющий судить о том, что одни облигации могут быть лучше других в смысле величины и частоты поступления денежных потоков.
Быть может, формулировка “средний срок окупаемости” подойдет нам больше? В определении срока окупаемости, принятом в корпоративных финансах, временная стоимость денег не учитывается. В этом случае можно показать, что если купонная доходность достаточно велика и близка к ставке дисконтирования, то сумма купонов, полученная за время равное дюрации будет сопоставима с ценой облигации.
Но еще более интересным примером является так называемая “вечная облигация” (или консоль), которая платит только купоны и не имеет номинальной погашаемой стоимости. Выражение дюрации Маколея для консоли, выплачивающей ежегодный купон С, легко вывести, используя стандартные методы анализа: D=(1+r)/r, где r — требуемая доходность при годовом начислении процентов. Цена такой облигации будет равна C/r. Теперь, если перейти к непрерывному начислению процентов (что не так грубо исказит картину, ведь консоли могут выплачивать купоны и ежемесячно), то D=1/y, где у — доходность при непрерывном начислении. И мы получим красивое соотношение: P=D·C, из которого ясно видно, что “вечная облигация” окупается ровно за D лет.
Если рассмотреть другой крайний пример для обычной купонной облигации, — предельно низкие (нулевые) ставки дисконтирования, то в этом случае ее цена равна сумме всех денежных потоков, а значит срок окупаемости должен быть равен времени до погашения. Можно показать, что в этом примере дюрация как правило не превосходит половину срока окупаемости. Не зря в некоторых источниках дюрацию иногда называют «временем полураспада» облигации. Так что, если понимать среднее именно как половину срока окупаемости, то это определение может нам и подойти.
Однако рассмотренный выше подход нас не вполне устраивает, ведь временная стоимость денег для нас имеет значение и полученные купоны мы обязательно реинвестируем. Для того, чтобы получить правильное соотношение для срока окупаемости, с ценой облигации нужно сравнивать не сумму купонов D·C, полученных за время, равное дюрации, а будущую стоимость аннуитета FV[C], рассчитанную для этих купонов. Поэтому, введем так называемый приведенный срок окупаемости PaybackRatio = FV[C]/P, который легко интерпретировать: если он равен или больше единицы, нам удалось отбить вложения в течение t=D, если нет, то увы.
В качестве примера на рис 1. приведены графики приведенных сроков окупаемости 10-летней облигации как функции ставки дисконтирования для различных значений купонной доходности (от 2.5% до 15%).
Видно, что зависимость довольно сложная и дюрация Маколея в нашем случае может выступать в качестве меры «окупаемости» только при достаточно высоких ставках дисконтирования, а в текущих рыночных условиях низких ставок эта мечта вряд ли достижима.
Подводя итог, можно сказать, что дюрация Маколея как «эффективный срок погашения» или «срок окупаемости» безупречно интерпретируется в двух случаях: 1) бескупонная облигация, 2) консоль. Для распространения этого подхода на привычную нам купонную облигацию желательны как высокие ставки дисконтирования, так и большой купонный доход.
И напоследок стоит уточнить, что понятие срока окупаемости, которое обычно применяется к инвестиционным проектам, теряет смысл в условиях торговли высоколиквидными облигациями на ОРЦБ, так как любую купленную облигацию можно продать по усмотрению инвестора в любой удобный момент и тем самым «окупить вложения».
Теперь немного усложним задачу и попросим тиньковскую домохозяйку с помощью известной нам формулы найти дюрацию Маколея, например, для флоатера ОФЗ-24020. И тут ее, скорее всего, постигнет неудача, ведь будущие купоны флоатера неизвестны и зависят от средних значений ставок Ruonia за купонный период, как это определено в спецификации бумаги. Их нельзя подставить в формулу для дюрации. Что делать, как быть?
Нам следует полностью изменить подход к дюрации и отказаться рассматривать ее исключительно с точки зрения средневзвешенного времени получения денежных потоков по облигации. Об этом поговорим в следующей главе.
Облигации: дюрация. Примеры и польза для частного инвестора
Не смотрите Википедию
Мы хотим, чтобы нам объясняли так, чтобы было понятно. Когда видишь формулу и формулировку дюрации в википедии, становится совсем непонятно.
Дюрация — средневзвешенный срок потока платежей, причём весами являются дисконтированные стоимости платежей.
Дюрация от слова Duration
Дюрация — термин, пришедший от английского слова duration — длительность.
И сразу становится логично, что данный показатель измеряется во временных единицах (обычно годы, могут быть дни).
В формуле дюрации важно понять ключевую часть:
D = Σi(PVi * ti) / Σi(PVi),
а Σi для тех кто забыл — это сумма из всех значений по i.
Пример
Возьмем 3 облигации с одинаковой доходностью:
D = 1 год * 1100 рублей (номинал + процент) / 1100 рублей = 1 год.
2. Облигация с номиналом 1000 рублей с купоном 1 раз в полгода 50 рублей:
D = 0.5 года * 50 рублей + 1 год * 1050 рублей / 1100 рублей = 0,97 года
3. Облигация с номиналом 1000 рублей и купоном 1 раз в квартал по 25 рублей:
D = 0.25 года * 25 рублей + 0.5 года * 25 рублей + 0.75 года * 25 рублей + 1 год * 1025 рублей / 1100 рублей = 0.96 года
Имея 3 облигации с одинаковой доходностью мы получаем разную дюрацию. Так о чем же говорит нам эта разница?
Смысл дюрации
Дюрация показывает среднее время, за которое мы полностью вернем свои вложения в облигации. Таким образом, при прочих равных условиях, нужно выбирать облигации с меньшей дюрацией (меньшим сроком возврата средств).
Представим ситуацию: К вам пришли 2 друга, оба хотят одолжить 100 000 рублей под 20% в год:
— первый отдаст вам 120 000 рублей разом через год;
— второй будет отдавать по 10 000 рублей в месяц.
Очевидно, что вам больше понравится второй вариант, так как вы свои деньги начнете получать назад уже через месяц. Дюрация во втором случае будет ниже.
Но в примере выше все и так очевидно и знать дюрацию не обязательно. А вот когда нужно выбрать из 5-10 примерно похожих по условиям облигациям, дюрация приходит на помощь.
Дюрация как мера риска
Продолжим наш пример: к вам пришли те же 2 друга, но они хотят взять 100 000 рублей не на 1 год, а на 10 лет и под все те же 20% годовых:
— первый отдаст вам всю сумму в конце года;
— второй также будет отдавать частями каждый месяц.
Дюрация во втором случае опять будет меньше — это понятно. Но на этот раз, возможно, вы подумаете, что вообще не стоит давать деньги друзьям, так как может случиться, что сейчас на 100 000 рублей вы со всей семьей поедете в отпуск, а через 10 лет на эти деньги, разве что купите продукты на вечер.
Временной фактор очень важен, так как 100 рублей сегодня НЕ РАВНЫ 100 рублям через год.
Сложная формула дюрации (из википедии) получается как раз потому, что она учитывает временной фактор и что 100 рублей сейчас НЕ РАВНЫ 100 рублям через 1 год. Поэтому в сложной формуле дюрации все поступления идут с поправочными коэффициентами (продисконтированы), зависящими от процентной ставки.
Из этого вытекает главное, что нужно понять:
Чем выше дюрация, тем выше неопределенность (риск) для инвестора.
На практике это оказывается очень интересно. Так как стоимость денег, как и сама дюрация, зависят от процентной ставки, собственно, как и тело облигации (а вы ведь знаете, что если ставки растут — облигации падают и наоборот), получается, что есть реальная связь между изменением процентной ставки и изменением стоимости облигации в зависимости от дюрации.
Изменение процентной ставки на 1% в любую сторону вызывает изменение стоимости облигации на процент равный дюрации в противоположную сторону.
— Облигации с дюрацией 2 упали на 2%
— Облигации с дюрацией 5 упали на 5%
— Облигации с дюрацией 10 упали на 10%
2. Понизили ставку на 6.5%
— Облигации с дюрацией 2 выросли на 13%
— Облигации с дюрацией 5 выросли на 32.5%
— Облигации с дюрацией 10 выросли на 65%
Как использовать дюрацию в инвестировании?
Практическая польза от понимания дюрации следующая:
Спасибо! Надеюсь эта статья покажется вам полезной — если так, пожалуйста поставьте лайк!
Если вам интересны подобные рассуждения, не вписывающиеся в формат полноценной статьи, подписывайтесь на мой телеграм канал.
Старался написать статью максимально понятно.
А Вы могли бы чуть подробнее объяснить,
1) почему Вы рассматриваете пример
Представим ситуацию: К вам пришли 2 друга, оба хотят одолжить 100 000 рублей под 20% в год:
— первый отдаст вам 120 000 рублей разом через год;
— второй будет отдавать по 10 000 рублей в месяц.
только с точки зрения дюрации? Там очевидно разные доходности.
2) Почему предлагаете
При прочих равных выбирать облигации с меньшей дюрацией.
Какие прочие равные имеются ввиду и почему такая рекомендация? Ниже Вы, например, пишете, что в зависимости от ожиданий по процентной ставке нужно выбирать ту или иную дюрацию. Вы не видите в этом противоречия?
только с точки зрения дюрации? Там очевидно разные доходности.
pessimist, конечно разная, но вовсе не она является в данном примере критерием для принятия решений. Автор судя по всему привык писать для Тинькоф-журнала, а публика там невзыскательная. Поверхностные рассуждения там примут на ура. С бурными аплодисментами. Но здесь все-таки форум профессионалов и тиньковские рецепты упрощения действительности не подойдут.
Автор в самом начале делает, например сразу два неверных утверждения
1.Дюрация показывает среднее время, за которое мы полностью вернем свои вложения в облигации.
2.Таким образом, при прочих равных условиях, нужно выбирать облигации с меньшей дюрацией (меньшим сроком возврата средств).
Инвестор из приведенного примера должен выбрать второй вариант потому что он сможет реинвестировать ежемесячные выплаты под ту же ставку (если не сказано ничего другого в данном модельном примере это нужно предположить) Иными словами, эффективная доходность второй инвестиции будет выше: не 20%, а 22%. (для вычислений можно пользоваться формулой ЭФФЕКТ в Excel)
Автор, скорее всего, не понимает различия между дюрацией Маколея (формулу которой он привел выше и назвал средним временем) и модифицированной дюрацией, которую нужно использовать при оценке риска. Она заведомо меньше. То есть он пишет, что
— Облигации с дюрацией 10 упали на 10%
На деле они упадут на 9%, если купон ежегодный. Ну и т.д. и т.п. Он даже не подчеркивает, что эти рассуждения могут касаться только простых купонных облигаций. А на рынке все больше появляется корпоративных облигаций с привязкой купона к чем-либо. Даже КАМАЗ наплодил целую серию облигацию с привязкой к КБД.
Можно было бы сказать, что это малосущественные придирки, однако это не так. Мы не тинькофские пульсята, накупившие бондов Норникеля, и не хотим попадать в ситуации, когда профанация финансовых знаний больно бьет по нашему кошельку.
Что такое дюрация облигаций
Что показывает и как рассчитать
Дюрация — это эффективный срок до погашения облигации. Эффективный срок учитывает все купонные платежи, выплаченные в разное время, и различные особенности облигации, такие как амортизация или оферта. Если купонных платежей, амортизации и оферты нет, то дюрация совпадает со сроком до погашения облигации.
Для чего нужна и где используется
С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций. Дюрация показывает зависимость облигаций от изменения процентных ставок, и это полезно при выборе облигаций.
Также дюрация позволяет оценить другие финансовые активы с фиксированными выплатами. Например, банки могут рассчитывать дюрацию кредитов и кредитных портфелей.
Как узнать дюрацию
Необязательно считать самостоятельно: значение можно посмотреть на справочных сайтах, например в облигационном разделе « Смарт-лаба », на cbonds.ru или rusbonds.ru.
Значение дюрации также есть в торговом терминале QUIK. Еще его можно посчитать для любой облигации в калькуляторе на сайте Московской биржи, в котором есть и обычная, и модифицированная дюрация.
Но мы все же рассмотрим несколько методик расчета.
Дюрация Маколея: формула расчета
Первый и наиболее известный способ расчета дюрации — формула Маколея. Дюрация Маколея показывает эффективный срок до погашения облигации.
Чтобы рассчитать дюрацию, надо сложить все будущие платежи с учетом срока их поступления и поделить результат на рыночную цену облигации с учетом накопленного купонного дохода. Будущие платежи по облигации — это купоны и погашение номинала частями или в конце срока.
В числителе мы складываем все денежные потоки: четыре купонных платежа и погашение номинала облигации. Так как это будущие платежи разного времени, нужно каким-то образом привести их к сегодняшнему дню. С точки зрения математики эти платежи надо освободить от 10% доходности, то есть дисконтировать. Дисконтирование — это процесс, обратный начислению процентов. В нашем случае ставка дисконтирования — это годовая доходность, то есть 10%.
Далее надо поделить это на цену облигации с НКД — и мы получим дюрацию.
Если купоны выплачиваются чаще раза в год, то расчет усложнится. Квартальных или полугодовых платежей больше, и их надо дисконтировать по квартальной или полугодовой ставке.
Модифицированная дюрация
Модифицированная дюрация — это второй способ измерения дюрации. С ее помощью инвестор определяет, на сколько процентов изменится цена облигации, если изменятся процентные ставки.
MD = Дюрация Маколея / (1 + процентная ставка)
Для небольших изменений работает следующая формула:
Изменение цены / Рыночная цена с НКД = −MD × Изменение ставок
Например, MD равна 3, цена облигации с учетом НКД — 95%, доходность к погашению — 8% годовых. Мы можем определить, как изменится цена, если доходность вырастет на 0,5 процентного пункта и станет равна 8,5%.
Х = −3 × 0,005 × 0,95 = −0,01425
Если доходность вырастет на 0,5%, цена облигации снизится на 1,4%.
Эффективная дюрация и оферта
Эффективная дюрация — третий способ измерить дюрацию. Подходит для облигаций, которые содержат встроенные условия — то есть эмитент может их выкупить раньше срока погашения по оферте. Вероятность того, что облигация будет выкуплена, сокращает ее дюрацию.
Дюрацию облигаций с офертой рассчитывают по формуле эффективной дюрации:
В числителе стоит разница между ценой облигации в условиях падения ставок и ее ценой при росте ставок. В знаменателе — первоначальная цена, умноженная на разницу ставок.
Например, у облигации Тинькофф 001Р-02R дюрация на 23 октября 2019 года составляет 674 дня, хотя срок обращения облигации — 3640 дней. Дюрация существенно меньше срока обращения, потому что по облигации предусмотрена оферта 4 апреля 2022 года и дюрация рассчитывается на момент оферты.
Дюрация портфеля облигаций
Дюрация портфеля облигаций — это средневзвешенная дюрация отдельных облигаций.
Например, в портфеле инвестора два вида облигаций — РЖД 001P-12R с дюрацией 1308 дней и ПИК БО-П03 с дюрацией 866 дней. Доли в портфеле — 70 и 30% соответственно.
ДПорт = 1308 × 0,7 + 866 × 0,3 = 915,6 + 259,8 = 1175,4 дня
Дюрация проекта
По экономическому смыслу дюрация проекта близка к показателю срока окупаемости проекта, но она учитывает только дисконтированные денежные потоки и не учитывает размер инвестиций.
Формула дюрации проекта:
Например, есть проект, который принесет по 500 Р в четвертый и пятый годы существования. Ставка дисконтирования зависит от многих факторов, например от риска инвестиций. В данном случае она составляет, допустим, 20%. Скорее всего, проект рискованный, поэтому по нему предлагают доходность выше, чем по надежным банковским депозитам. Рассчитаем дюрацию этого проекта.
Таким образом, без учета первоначальных вложений проект окупится через четыре года и пять с половиной месяцев.
Свойства дюрации
Дюрация купонных облигаций меньше времени до погашения, потому что инвестор регулярно получает купонные платежи.
Дюрация дисконтных облигаций равна времени до погашения, потому что по дисконтным облигациям инвесторы не получают купоны. Если купон один и выплачивается при погашении, дюрация также будет равна сроку до погашения.
При прочих равных чем меньше купон по облигации, чем реже его выплачивают или чем больше времени до погашения, тем больше дюрация: инвестор будет дольше возвращать свои деньги. И наоборот: если купонные платежи большие и более частые, а времени до погашения немного, то дюрация будет меньше, потому что инвестор быстрее вернет свои деньги.
Если рыночная цена облигации падает, то ее доходность растет и дюрация уменьшается, потому что инвестор покупает облигацию дешевле и возвращает вложения быстрее. И наоборот: если рыночная цена облигации растет, то ее доходность падает, а дюрация увеличивается, потому что инвестор больше платит за покупку и медленнее возвращает вложенные деньги.
Зависимость от процентных ставок
Если купонные платежи по облигациям зафиксированы, то риск для инвесторов заключается в колебаниях цены облигации. Цена облигации и процентные ставки связаны обратной зависимостью: если процентные ставки в экономике растут, то цена ранее выпущенных облигаций падает, и наоборот.
Чем меньше дюрация, тем меньше цена облигации изменится при изменении процентных ставок. Например, по облигациям Тинькофф БО-07 на 23 октября 2019 года дюрация всего 64 дня, потому что 30 декабря банк погасит облигации по номиналу. Скорее всего, за оставшиеся несколько месяцев цена облигации практически не поменяется.
И наоборот: чем выше дюрация, тем больше вероятность того, что цена облигаций существенно изменится при изменении процентных ставок. Например, по облигациям РЖД 001P-12R на 23 октября дюрация составляет 1308 дней, или 3,6 года. За несколько лет ставки могут измениться, а значит, и цена облигации изменится.
Что такое выпуклость облигаций и как она связана с дюрацией
Зависимость цены облигации от ее доходности не линейная, а выпуклая. Выпуклость облигаций бывает позитивной и негативной, а точное значение выпуклости для конкретных облигаций можно посмотреть на rusbonds.ru. В некоторых источниках выпуклость называют конвекцией.
На графике цена облигации C с негативной выпуклостью — желтая линия — при росте ставки меняется, а при падении ставки остается стабильной. Оценка таких облигаций с помощью дюрации дает очень большую погрешность из-за асимметрии между ценой и доходностью облигации. На графике асимметрия — это расстояние между пунктирной и сплошными линиями, которое увеличивается из-за выпуклости. Поэтому при больших изменениях процентной ставки используют выпуклость.
Профессиональные управляющие используют выпуклость для оценки инвестиционных портфелей. Частным инвесторам выпуклость может быть полезна, если дюрация облигаций одинаковая.
На рисунке дюрация двух облигаций с позитивной выпуклостью — красная и зеленая линии — одинаковая, но выпуклость облигации А больше, чем у облигации В. При падении ключевой ставки ЦБ цена облигации А вырастет больше, чем цена облигации В. При росте ключевой ставки ЦБ цена облигации А упадет меньше, чем цена облигации В. Таким образом, более выпуклая облигация А выгоднее для инвестора.
Как применять дюрацию на практике
На практике с помощью модифицированной дюрации вычисляют, как изменится цена облигации при изменении рыночных процентных ставок.
Например, доходность облигации к погашению — 12%, а модифицированная дюрация — 3,469. Мы можем определить, как изменится цена облигации при росте рыночных ставок на 1%:
−3,469 × 0,01 / 1,12 = −0,031 = −3,1%
При росте ставок на 1% цена этой облигации снизится на 3,1%.
С помощью обычной дюрации инвесторы сравнивают похожие облигации и выбирают ту, у которой дюрация меньше. Так можно уменьшить процентный риск.
Если инвестор полагает, что процентные ставки в экономике будут снижаться, разумно купить облигации с большим сроком погашения и, соответственно, большей дюрацией. Цена таких облигаций вырастет, а кроме того, по ним по-прежнему будут выплачиваться более высокие купоны, чем по новым облигациям.
Напротив, если ожидается повышение процентных ставок, облигации с меньшей дюрацией могут оказаться более подходящими, так как их цена снизится в меньшей степени.
Использование дюрации для оценки риска облигаций. Чтобы уменьшить процентный риск, инвестор выбирает облигации с низкой дюрацией или формирует портфель с заданной дюрацией.
Например, инвестор хочет составить портфель из двух видов облигаций — с дюрациями 3,4 и 5,6 года — и застраховаться от риска изменения процентных ставок на 5 лет. Инвестор не может повлиять на изменение рыночных процентных ставок, но на время дюрации он получает гарантированный купонный доход. Если рыночные ставки растут, то цена облигаций падает. Инвестор реинвестирует купоны под более высокий процент и этим компенсирует падение цены облигации. Таким образом, для страхования риска инвестор должен составить портфель с дюрацией 5 лет и определить доли облигаций.
Доля облигаций А + Доля облигаций В = 100%
Дюрация портфеля = Доля А × 3,4 + Доля В × 5,6 = 5 лет
Доля облигаций А = 27%
Доля облигаций В = 73%
Эта техника называется иммунизацией портфеля, и она работает для небольших изменений процентных ставок.
На три вещи можно смотреть бесконечно: как горит огонь, как течет вода и НА ДЮРАЦИЮ
Прекрасный разбор, многое стало понятным
«Простыми словами — это количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги».
Юлия, это неправильное определение, хотя оно и встречается довольно часто.
Представьте себе облигации с доходностью в 10% годовых без амортизации. В соответствии с этим определением, дюрация всех облигаций со сроком более 10 лет будет одинаковой. А это не так. Например, если срок до погашения 10 и 100 лет, то дюрация будет отличаться весьма значительно. Взгляните, хотя бы, на формулу Маколея.
Влад, ну а как было иначе простыми словами сказать иначе, чтобы основная мысль была понятна?
Юлия! Вы гений! Сейчас прочитал новый вариант первого абзаца. Именно так и следует писать.
Влад, это работа коллективного разума 🙂
1) количественного измерения процентного риска
2) иммунизации портфеля, составленного из процентных активов и обязательств.
Я очень ценю Ваши усилия по ведению блога по вкладам и налогам, это сложная и кропотливая работа, и она выполняется блестяще. Но когда мы говорим о терминах и понятиях из мира финансов, то поскольку у Вас нет опыта работы в этой области, Ваше понимание складывается из прочтения популярных статей на различных сайтах.
Для того чтобы расширить свои знания, необходимо читать больше профессиональной литературы по тематике фиксированного дохода. Начать можно, например, с корифеев :
Fabozzi Frank J. (ed.) The Handbook of Fixed Income Securities (здесь он прямо критикует отношение к дюрации как «среднему сроку до погашения» и т.д.)
Fabozzi Frank J. Bond Markets, Analysis and Strategies, 8e
Choudhry M. An Introduction to Bond Markets, 4e
Простой пример: Вы не сможете определить дюрацию флоатера по Вашим формулам, тем не менее она существует. Дюрация может быть как больше срока до погашения, так и даже отрицательной. Ваши формулы этого не объяснят. Так происходит потому, что Вы просто забываете, что мир облигаций не сводится к инструментам, выплачивающим фиксированный размер купона и номинал.
Вячеслав, я практик, не теоретик. И теоретиком становиться не собираюсь, как и все читатели моего блога. Я когда-то пробовал читать Фрэнка Фабоцци (Рынок облигаций: Анализ и стратегии. 2-е изд., испр. и доп.: Альпина Бизнес Букс; Москва; 2007) (уж извините, но «my english isn’t well enough»). Ничего кроме скуки он не вызвал. Я не понял как мне в моей практической деятельности использовать то, про что он пишет.
Я не собираюсь рассчитывать дюрацию флоатера или линкера или даже банального ОФЗ-ПД, по той причине, что это за меня делает мосбиржа. Мне важно более-менее понимать что это такое и знать как это использовать. И этого мне достаточно. Я же не предлагаю вам читать больше профессиональной литературы по гидродинамике, на основании того, что вы пользуетесь водопроводом.
BAY, Эх, ну что тут сказать. «Не хочу учиться, а хочу жениться» Раз Вы не нашли пользу в чтении Фабоцци, то, безусловно, соглашусь, что пытаться переубедить Вас большого смысла нет. Вы упрямо отстаиваете свое право на простую картину мира и я бесконечно уважаю Ваш выбор.
«Я не собираюсь рассчитывать дюрацию флоатера или линкера или даже банального ОФЗ-ПД, по той причине, что это за меня делает мосбиржа. «
Мосбиржа рассчитывает дюрацию Маколея (так же как, впрочем и доходность) для флоутера или линкера некорректно, так как исходит из того, что текущий купон будет оставаться таким и в дальнейшем, тогда как на самом деле будущие купоны для этих облигаций неизвестны. Впрочем, все это специально оговаривается и в большинстве бонд-калькуляторов у таких облигаций в графах дюрации и дох-ти стоят прочерки.
«.. я практик, не теоретик. И теоретиком становиться не собираюсь..»
Все, что я написал имеет непосредственное практическое отношение к реальности, но, соглашусь, неприхотливому инвестору в ОФЗ-ПД вряд ли пригодиться. Хотя, как знать. Если бы инвесторы всматривались в мир облигаций чуть пристальней, чем они это делают при помощи моб. приложений, они бы с осторожностью отнеслись к покупке облигаций «Норильского Никеля» с встроенным опционом-колл и не потеряли бы свои деньги при досрочном погашении.
«Мне важно более-менее понимать что это такое и знать как это использовать. И этого мне достаточно. «
Но я пишу эти комментарии не только для Вас (мы же выяснили, что Вы не занудный теоретик, а инвестор с практичным складом ума) но и для тех читателей, кому быть может интересно подробнее разобраться в мире облигаций, их свойствах и особенностях.