е равно мс в квадрате что это за формула
E = mc²: Самое знаменитое уравнение Эйнштейна
Это гораздо больше, чем взаимосвязь массы-энергии, это ключ к пониманию квантовой Вселенной.
В течение сотен лет существовал непреложный закон физики, который никогда не оспаривался: при любой реакции, происходящей во Вселенной, масса вещества сохранялась. Независимо от того, что с чем реагирует, масса исходных веществ и масса получившихся будет равна. Но, по законам специальной теории относительности, масса просто не может быть конечной сохраненной величиной, так как разные наблюдатели не соглашались бы с тем, что такое энергия системы. Вместо этого Эйнштейн смог получить закон, который мы используем сегодня, управляемый одним из самых простых, но самых мощных и изящных уравнений из всех существующих:
В самом известном уравнении Эйнштейна есть только три составляющих:
Это уравнение полностью меняет мир. Как выразился сам Эйнштейн:
Из специальной теории относительности следует, что масса и энергия — это одновременно разные проявления одного и того же — несколько необычная концепция для среднего ума.
Вот три самых важных по значимости вывода, которые следуют из этого простого уравнения:
Факт эквивалентности массы-энергии привел Эйнштейна к его величайшему достижению: Общей теории относительности. Представьте, что у вас есть частица материи и частица антивещества, каждая из которых имеет одинаковую массу покоя. Вы можете уничтожить их, и они будут производить фотоны определенного количества энергии, точного количества, заданного формулой E=mc². Теперь представьте, что пара частиц/античастиц движется очень быстро, как будто они падают из космоса, а затем самоуничтожаются вблизи поверхности Земли. Эти фотоны теперь будут иметь дополнительную энергию: не только E от E = mc², но и дополнительную E от количества кинетической энергии, которую они получили при падении.
Если мы хотим сохранить энергию, мы должны понять, что гравитационное красное смещение (а также синее смещение) должно быть реальным. Теория всемирного тяготения Ньютона не может объяснить этого, но в Общей теории относительности Эйнштейна кривизна пространства означает, что попадание в гравитационное поле заставляет вас получать энергию, а выход из гравитационного поля заставляет вас терять энергию. Тогда полное и общее отношение для любого движущегося объекта — это не только E=mc², но и E²=m²c⁴+ p²c² (где p — импульс.) Только обобщая вещи, включающие энергию, импульс и гравитацию, мы можем действительно описать Вселенную.
Е равно мс в квадрате что это за формула
Знаменитая формула на небоскрёбе Тайбэй 101 во время одного из мероприятий Всемирного года физики (2005)
E=mc² — уравнение, которое в теоретической физике устанавливает взаимосвязь между энергией (E), в любой форме, и массой (m). В этой формуле 
, квадрат скорости света в вакууме, является постоянным множителем, переводящим массу в энергию. Например E (джоули) = M (килограммы) · (299792458(метры в секунду))². Популярный, и известный многим, вид формулы E=mc², является неудачным, так как речь идет не о всякой энергии, а о энергии покоя Е0. Т. о. следует писать формулу следующим образом Е0=mc 2
Основы
применимо ко всем объектам с массой или энергией, так как оно утверждает, что масса происходит из энергии, или энергия из массы, и что одно можно превращать в другое, что является основой ядерной энергии.
Обычно это уравнение применяется к объекту, который покоится по отношению к системе отсчёта. Но тот же объект может считаться движущимся с точки зрения другой системы отсчёта, так что уравнение всё равно действительно, но полная энергия (или, эквивалентно, масса) различается по величине в разных системах отсчёта. То есть в отличие от ньютоновской механики, в специальной теории относительности, релятивистская масса различна в различных системах отсчёта.
Для осознания этого надо понять, что существует два разных понятия для слова «масса». Например в одном смысле масса означает обычную массу, которую можно измерить, находясь в покое относительно массы. Это понятие массы покоя, которое обозначается как .
Изучавшим физику знакома ньютоновская формула кинетической энергии : . Это, по сути, то же самое, что и знаменитая формула Эйнштэйна, несмотря на совсем другой вид. В своей специальной теории относительности Эйнштейн обнаружил, что единственно правильным выражением для энергии движущегося тела является
Релятивистская масса
Математические формулы будут проще, если мы определим другой тип массы. Релятивистская масса определяется как
,
Следует отметить, что физического смысла ввода массы подобного сорта — нет! Более того масса, зависящая от скорости — «безобразна». См., к примеру, статью Окуня Л. Б. в журнале «Успехи фических наук» (УФН)Выпуск 7, 1989 или см. http://www.ufn.ru/ufn89/ufn89_7/Russian/r897f.pdf ===
Используя эту формулу для массы, мы может записать . Теперь до тех пор, пока скорости не станут сравнимы со скоростью света, эта релятивистская масса почти точно равна массе покоя. То есть, если задать , то получим что .
Для понимания различия между массой покоя и релятивистской массой необходимо переписать уравнение в названии статьи либо как при , либо как при .
В оригинальных статьях Эйнштейна (см. напр. [1]) m обозначает то, что сейчас назвали бы релятивистской массой. Когда современный физик говорит о «массе», он или она почти наверняка говорит о массе покоя. Это может служить причиной непонимания.
Приближение малых скоростей
Для скоростей, значительно меньших скорости света можно переписать точное уравнение в виде приближенного уравнения:
Таким образом видно, что ньютоновская формула для кинетической энергии просто пренебрегает той частью, о которой Ньютон ничего не знал — . Это могло произойти только из-за того, что Ньютон мог наблюдать объекты, движущиеся со скоростями малыми по сравнению со скоростью света, и вообще не мог наблюдать превращение массы в энергию, как это происходит в ядерных процессах. Эйнштейну потребовалось добавить дополнительный член, чтобы сделать формулу верной и при высоких скоростях. Сделав это он открыл, что масса может превращаться в энергию.
Интересно заметить, что поскольку член является константой, его можно включить в ньютоновскую механику, так как только изменения в энергии имеют какое-либо влияние на то, что происходит с телами. Это было бы большой потерей времени и усилий, хотя именно потому, что этот член не имеет никакого значения до тех пор, пока мы не рассматриваем такие вещи, как ядерные реакции. Те члены высшего порядка, которые мы отбросили, показывают, что относительность является поправкой высших порядков к ньютоновской механике. Ньютоновская механика на самом деле неверна, но достаточно близка к действительности при маленьких скоростях, можно сказать, что ньютонова механика применима при скоростях много меньших скорости света.
Значения формулы
В ньютоновской механике масса не переходит в энергию, поэтому массу покоя можно не принимать во внимание.
С другой стороны, тело, не обладающее массой покоя, как например фотон, может обладать энергией и поэтому иметь «массу» m=E/c², в частности участвовать в гравитационном взаимодействии.
История и последствия
Впервые формула появилась в 1900 году в статье Анри Пуанкаре, при описании эквивалентной массы излучения.
Альберт Эйнштейн вывел формулу, основываясь на своём исследовании от 1905 года о поведении объекта, движущегося с около световой скоростью. Знаменитое заключение, которое он вывел из исследования состоит в том, что масса тела является мерой его энергии покоя. Для осознания значимости этого утверждения необходимо сравнить электромагнитные силы с гравитационными силами. В электромагнетизме энергия содержится в полях (электрическом и магнитном), связанных с силами, а не с зарядами. В гравитации энергия содержится в самой материи. Тот факт, что масса искривляет пространство, в то время как заряды трёх других фундаментальных сил не искривляют, не является случайностью.
Энергия покоя = Масса×(скорость света)²
Согласно уравнению, максимальная энергия, которую можно получить от объекта, равна массе объекта, помноженной на квадрат скорости света.
Это уравнение было краеугольным камнем в создании атомной бомбы. Измеряя массу разных атомных ядер и вычитая из этого числа полную массу протонов и нейтронов, которую они имели бы поотдельности, можно получить оценку энергии связи, доступной в данном атомном ядре. Это не только показало, что возможно высвободить эту энергию путем слияния лёгких ядер или деления тяжёлых ядер, но и позволило оценить количество энергии связи, доступной для высвобождения. Следует отметить, что массы протонов и нейтронов тоже представляют собой энергию.
Менее известен тот незначительный факт, что Эйнштейн первоначально записал своё уравнение в форме (с обозначением энергии в виде «» вместо «», которое обозначало энергию в другом месте статьи).
Пример
Килограмм массы полностью превращается в
Важно отметить, что в практических применениях превращение массы в энергию редко происходит со стопроцентной эффективностью. Теоретически совершенным превращением было бы столкновение материи с антиматерией, однако в большинстве случаев вместо энергии возникают побочные продукты и вследствие этого только очень малое количество массы превращается в энергию. На самом деле, согласно уравнению, масса и есть энергия, но в целях краткости далее будет использоваться слово превращение.
Эйнштейн и его статья 1905 года
В этой статье говорится: «Если тело отдаёт энергию в виде L в виде излучения, его масса уменьшается на .», при этом излучение является кинетической энергией, и масса является понятием обыкновенной массы, использовавшемся в то время, тем же, что сегодня называется энергией покоя, либо инвариантной массой, в зависимости от контекста.
Именно разность масс ‘‘ до и после ухода энергии равна , а не полная масса тела ‘‘. В то время это было теоретическим заключением и не было проверено экспериментально.
Вклад других
Телевизионная биография
E=mc² использовалось в качестве названия вышедшей в 2005 году телевизионной биографии Эйнштейна, исследующей 1905 год.
Однако
Теория относительности, пришедшая ей на смену, и постулировала (вопреки популярной формулировке — «все относительно») постоянство скорости света. Согласно Эйнштейну, никакое тело или сигнал перемещаться быстрее не может, а сам свет преодолевает за секунду путь в 299792 километра в любой системе отсчета и в любом месте Вселенной. С этим спорили, но главным предметом спора были как раз «традиционные ценности» — постоянство масс, длин и временных интервалов, без чего стройная механистическая картина мира разрушалась. В двадцатом веке астрономические эксперименты подтвердили правоту Эйнштейна. В двадцать первом — поставили под сомнение то, в чем сам «отец новой физики» не успел усомниться.
Первыми про старение констант заговорили астрофизики. В их распоряжении были фотоснимки самых старых объектов во Вселенной — а именно, квазаров, которые находятся на периферии видимого пространства. Это значит, что свет, который фиксируют приборы, возник всего через 1-2 миллиарда лет после Большого Взрыва. В 1998 году обнаружилось, что спектр квазара — после всех поправок на допплеровское смещение — выглядел иначе, чем при «лабораторном» анализе веществ, из которых состоит космический объект. По положению линий в атомных спектрах может быть рассчитана постоянная тонкой структуры («альфа») — безразмерная величина, связывающая заряд электрона с константой Планка и скоростью света. Согласно результатам Джона Вебба и Виктора Фламбаума, за 12 миллиардов лет «альфа» увеличилась на несколько миллионных долей.
Речь, разумеется, шла не просто о росте или убыли отдельной величины. Если в боровской модели атома ей приписывали конкретный физический смысл — «орбитальной скорости» электрона на заданной «орбите» в единицах скорости света, то в современной теории элементарных частиц «альфа» служит параметром, определяющим природу электромагнитных явлений как таковых. Если бы «в начале времен» он отличался от нынешней величины на 4 процента, не происходило бы синтеза углерода в недрах звезд, и жизни не из чего было бы возникнуть. (Кстати, этот факт крайне популярен среди сторонников антропного принципа — утверждения о том, что Вселенная не могла бы быть иной, чем необходимо для появления разумных существ). И, конечно, еще больше возражений вызывала интерпретация «дефекта»: поскольку изменяться заряду электрона запрещают законы сохранения, пострадать должна либо скорость света, либо константа Планка. По ряду причин последнюю версию отбросили, так что под угрозой оказалась уже эйнштейновская теория.
С другой стороны, отнюдь не все физики восприняли известие как катастрофу. Многие были убеждены, что только теперь можно с уверенностью изучать «первые дни» после Большого Взрыва. Термодинамика не в состоянии объяснить, как между различными частями Вселенной установилось тепловое равновесие — для этого отдаленные участки должны были обмениваться по крайней мере излучением, но лимит на скорость его распространения делал такой обмен невозможным. Если же скорость света раньше была «сверхсветовой», причины равновесия становятся понятны.
В этом, в свою очередь, увидели надежду на подтверждение теории струн — гипотезы (или, точнее, семейства гипотез), расширяющей «эйнштейновское» четырехмерное пространство-время до десятков измерений. Вместо частиц расширенное пространство населяют «струны» или «мембраны», колеблющиеся в дополнительных размерностях. «Колебаниям» с определенной частотой отвечают различные свойства «настоящих» частиц. Лишние измерения обладают сложной геометрией, замкнуты и ограничены (а потому — ненаблюдаемы), в отличие от времени и пространства, открытых и бесконечных в первом приближении. Благо математикам такие объекты знакомы и интересны, теория бурно развивалась последние несколько десятилетий, хотя и не получила серьезных экспериментальных подтверждений.
Перспективы выглядят заманчиво: «струны» должны объединить два главных достижения «новой физики» — гравитационную и квантовую теории. Приверженцы этих взглядов готовились узнать о первых «практических» результатах после запуска Большого адронного коллайдера — самого мощного из ускорителей элементарных частиц. События на краю космоса, разумеется, не отменяют земных опытов, однако лишают их статуса «последней надежды». Если масса протона действительно меняется со временем, это можно трактовать как расширение Вселенной, но только в дополнительных размерностях — тех самых, которые опасались не найти.
Что, впрочем, не делает менее неуютной мысль, что ничего абсолютного в этой Вселенной нет.
См. также
Ссылки
ar:ط=ك.س² bg:E=mc² br:E=mc² ca:E=mc² cs:E=mc² da:E=mc² de:Äquivalenz von Masse und Energie en:E=mc² es:E=mc² et:E=mc² eu:E=mc² fa:E=mc² fi:E=mc² fr:E=mc² he:E=mc² hu:E=mc² id:E=mc² it:E=mc² ja:E=mc² ko:E=mc² la:E=mc² lad:E=mc² nap:E=mc² nl:Massa-energierelatie nn:E=mc² no:Masseenergiloven pl:Równoważność masy i energii pt:E=mc² scn:E=mc² sl:E=mc² sr:E=mc² sv:E=mc² tr:E=mc² zh:E=mc²
Спросите Итана №78: почему E = mc2?
Самое знаменитое уравнение Эйнштейна вычисляется более красиво, чем это можно было бы ожидать.
Из специальной теории относительности вытекает, что масса и энергия являются разными проявлениями одного и того же – концепция, среднему уму незнакомая.
— Альберт Эйнштейн
Некоторые научные концепции настолько меняют мир и настолько глубоки, что практически каждый знает о них, даже если полностью и не понимает. Почему бы не поработать над этим вместе? Каждую неделю вы отправляете ваши вопросы и предложения, и на этой неделе я выбрал вопрос Марка Лиюва, который спрашивает:
Если бы наша Вселенная не была устроена так, как сейчас, то всё могло бы быть по-другому. Давайте посмотрим, что я имею в виду.
С одной стороны, у нас имеются объекты с массой: от галактик, звёзд и планет до самых мелких молекул, атомов и фундаментальных частиц. Хотя они и крохотные, у каждой из компонент того, что известно нам под именем материи, имеется фундаментальное свойство массы, что означает, что даже если исключить его движение, даже если замедлить его до полной остановки, он всё равно будет оказывать влияние на все остальные объекты Вселенной.
Конкретно, он оказывает гравитационное притяжение на всё остальное во Вселенной, неважно, на каком расстоянии находится удалённый объект. Он притягивает всё к себе, испытывает притяжение ко всему остальному, а также обладает энергией, присущей самому его существованию.
Последнее утверждение контринтуитивно, поскольку об энергии, по крайней мере, в физике, говорят, как о возможности что-либо сделать – о возможности совершать работу. А что можно сделать, если ты просто сидишь на месте?
Перед тем, как ответить, давайте посмотрим на другую сторону монеты – вещи без массы.
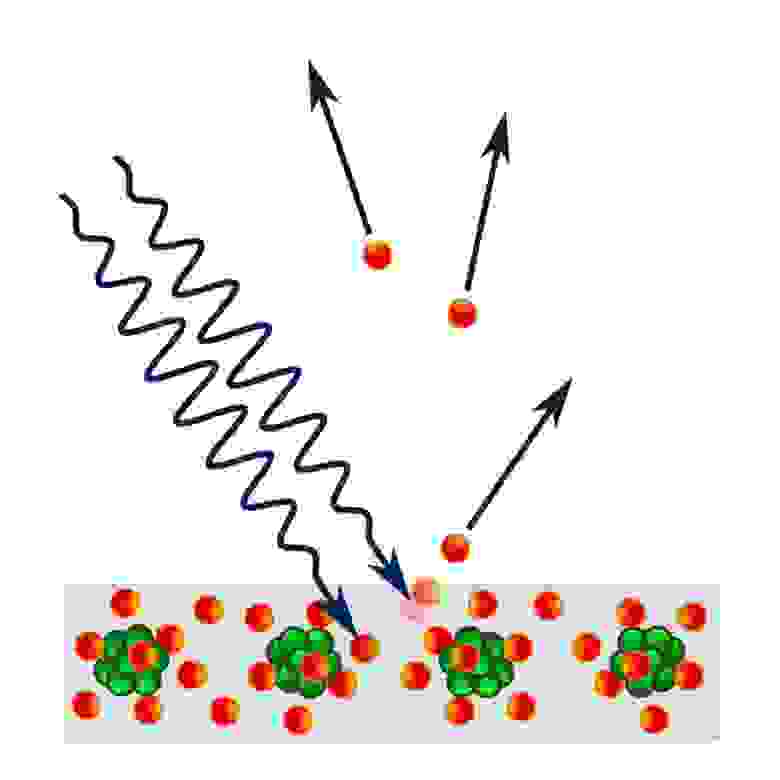
С другой стороны, существуют вещи, не имеющие массы – например, свет. У этих частиц есть определённая энергия, и это легко понять, наблюдая их взаимодействие с другими вещами – при поглощении свет передаёт им свою энергию. Свет с достаточной энергией может разогревать материю, добавлять кинетическую энергию (и скорость), вышибать электроны на верхние энергетические уровни или вообще ионизировать, в зависимости от энергии.
Более того, количество энергии, содержащейся в безмассовой частице, определяется только её частотой и длиной волны, произведение которых всегда равняется скорости движения частицы: скорости света. Значит, у более длинных волн частоты меньше, и энергия меньше, а у коротких – частоты и энергия выше. Массивную частицу можно замедлить, а попытки отобрать энергию у безмассовой приведут лишь к удлинению её волны, а не к изменению скорости.
Изначально коробочка не двигается, но поскольку фотоны обладают энергией (и импульсом), когда фотон сталкивается с зеркалом с одной стороны коробки и отскакивает, коробка начнёт движение в том направлении, в котором изначально двигался фотон. Когда фотон достигнет другой стороны, он отразится от зеркала с другой стороны, изменяя импульс коробки обратно до нуля. И он продолжит отражаться таким образом, в то время как коробка половину времени будет двигаться в одну сторону, а другую половину – оставаться неподвижной.
В среднем коробка будет двигаться и, следовательно, так как у неё есть масса, будет иметь определённую кинетическую энергию, благодаря энергии фотона. Но важно также помнить про импульс, количество движения объекта. Импульс фотонов связан с их энергией и длиной волны очень просто: чем короче волна и выше энергия, тем выше импульс.
Подумаем о том, что это значит, и для этого проведём ещё один эксперимент. Представьте, что происходит, когда изначально двигается только сам фотон. У него будет определённое количество энергии и импульс. Оба свойства должны сохраняться, поэтому в начальный момент энергия фотона определена его длиной волны, а у коробки есть только энергия покоя – какая бы она ни была – и фотон обладает всем импульсом системы, а у коробки импульс нулевой.
Затем фотон сталкивается с коробкой и временно поглощается. Импульс и энергия должны сохраняться – это основные законы сохранения Вселенной. Если фотон поглощён, то существует только один способ сохранить импульс – коробка должна двигаться с определённой скоростью в том же направлении, в котором двигался фотон.
Проблема? Нет, это довольно просто решить. Энергия системы коробка/фотон равна массе покоя коробки плюс кинетической энергии коробки плюс энергии фотона. Когда коробка поглощает фотон, большая часть его энергии переходит в увеличение массы коробки. Когда коробка поглотила фотон, её масса меняется (увеличивается) по сравнению с той, что была до столкновения.
Спросите Итана: по какой фундаментальной причине E = mc²?
Альберт Эйнштейн в 1920 году. Хотя он и совершил множество прорывов в физике, от специальной и общей теорий относительности до фотоэлектрического эффекта и статистической механики, многие задачи он решить не сумел. Самым его знаменитым уравнением остаётся E = mc².
Спросите любого человека, даже не разбирающегося в науке, о достижениях Эйнштейна, и вам приведут в пример самое его знаменитое уравнение: E = mc². Проще говоря, оно означает, что энергия равняется массе, перемноженной с квадратом скорости света. И это очень многое говорит о нашей Вселенной. Единственное уравнение говорит о том, сколько энергии содержится в массивной частице в состоянии покоя, и сколько энергии требуется для создания частиц и античастиц. Оно говорит нам о том, сколько энергии высвобождается в ядерных реакциях, и сколько энергии порождает аннигиляция материи с антиматерией.
Но почему? Почему энергия равняется массе, перемноженной с квадратом скорости света? Почему не как-то иначе? Об этом спрашивает наш читатель:
Уравнение Эйнштейна потрясающе элегантное. Но реальна ли его простота, или же только кажется? Выводится ли оно напрямую из эквивалентности энергии любой массы и квадрата скорости света (а это вообще кажется удивительным совпадением)? Или оно существует только потому, что его члены определены удобным способом?
Отличный вопрос. Давайте исследуем самое знаменитое уравнение Эйнштейна, и посмотрим, почему оно не могло быть другим.
Подготовка к испытаниям ракеты с ядерным двигателем, 1967. Она работает на преобразовании массы в энергию, в основе которого лежит знаменитое уравнение E = mc².
Для начала нужно кое-что понять касательно энергии. Её очень сложно определить, особенно далёкому от физики человеку. Навскидку мы можем придумать несколько примеров.
Фотоэлектрический эффект описывает ионизацию электронов фотонами в зависимости от длин волн отдельных фотонов, а не от интенсивности света, суммарной энергии или какого-либо ещё свойства. Если у кванта света достаточно энергии, он может взаимодействовать с электроном, ионизировав его, выбив его из материала, что даст сигнал, который можно обнаружить. Такие фотоны переносят энергию и выполняют работу над ударяемыми ими электронами.
У работы есть своё физическое определение: это сила, прикладываемая в направлении, совпадающем с направлением движения предмета, умноженная на расстояние его перемещения. Поднятие штанги на определённую высоту требует провести работу против силы гравитации, и увеличивает гравитационную потенциальную энергию. Отпустив штангу, мы преобразуем её гравитационную потенциальную энергию в кинетическую. Ударяющая пол штанга преобразует кинетическую энергию в комбинацию из тепловой, механической и звуковой энергии. Энергия в этих процессах не создаётся и не уничтожается, а преобразуется из одной формы в другую.
Большинство людей размышляют о формуле E = mc² в терминах анализа размерностей. Они говорят: так, энергия измеряется в Джоулях, а Джоуль – это килограмм на метр в квадрате на секунду в квадрате. Поэтому, чтобы превратить массу в энергию, нужно умножить это на метр в квадрате, делённый на секунду в квадрате. При этом у нас есть фундаментальная константа с размерностью метр/секунда. Эти рассуждения разумны, но не достаточны.
Ведь вы можете измерять любую скорость в метрах в секунду, а не только скорость света. Кроме того, природе никто не запрещает выдать пропорциональную константу – какой-нибудь множитель типа ½, ¾, 2π, и т.п., чтобы сделать уравнение верным. Чтобы понять, почему уравнение должно выглядеть, как E = mc², и почему других вариантов быть не может, нам надо представить физическую ситуацию, в которой можно будет различить разные интерпретации. Такой теоретический инструмент известен, как «мысленный эксперимент» (или gedankenexperiment, как сказал бы Эйнштейн), и стал одной из великих идей, появившихся в голове Эйнштейна и укоренившихся в научном мейнстриме.
Мы можем представить, что у частицы есть энергия, присущая её массе покоя, и энергия её движения – кинетическая. Можно представить, что частица начала свой путь, находясь высоко в гравитационном поле, то есть с большим запасом потенциальной энергии, но изначально не двигалась. Если мы её уроним, потенциальная энергия превратится в кинетическую, а энергия массы покоя останется той же. Перед самым ударом о землю никакой потенциальной энергии у неё не останется – только кинетическая и энергия массы покоя, какие бы они ни были.
У обозначенной оранжевым частицы, покоящейся над поверхностью земли, не будет кинетической энергии, но будет большой запас потенциальной. Если её отправить в свободное падение, она приобретёт кинетическую энергию, в которую превратится потенциальная.
Теперь добавим ещё одну идею: что у всех частиц есть двойники-античастицы, и что когда они сталкиваются друг с другом, то аннигилируют, выделяя чистую энергию.
Да, E = mc² описывает взаимоотношение массы и энергии, включая количество энергии, необходимое для создания из ничего пар частица-античастица, и то, сколько энергии вы получите, когда такая пара аннигилирует. Но мы пока этого не знаем, мы хотим это доказать!
Давайте представим, что у нас не одна частица находится высоко в гравитационном поле, а сразу и частица, и античастица, и они готовы упасть. Рассмотрим два разных сценария развития, и изучим их последствия.
Появление пар частица-античастица (слева) из чистой энергии – реакция полностью обратимая (справа), они могут аннигилировать, превратившись в энергию. Но для многих систем частиц обратимость не гарантирована.
Сценарий 1: частица и античастица падают, и аннигилируют прямо перед ударом о землю. Ситуация похожа на описанную ранее, просто мы её удвоили. И частица, и античастица начинали с некоего количества энергии массы покоя. Мы не знаем, сколько её было, просто знаем, что у частицы и античастицы они одинаковые, поскольку массы частиц идентичны массам соответствующих античастиц.
Теперь они обе падают, превращая потенциальную гравитационную энергию в кинетическую, в дополнение к их энергии массы покоя. Как и в предыдущем случае, перед ударом о землю вся их энергия заключена в двух видах – энергии массы покоя и кинетической. Только теперь перед самым столкновением они аннигилируют, превращаясь в два фотона, общая энергия которых должна равняться сумме энергий массы покоя и кинетических энергий обеих частиц.
Однако для фотона, массы не имеющего, энергия описывается одним только импульсом, помноженным на скорость света: E = pc. Какой бы ни была энергия обеих частиц перед столкновением с землёй, энергия этих фотонов должна в сумме давать сумму энергий частиц.
Если пара частица-античастица аннигилирует в чистую энергию (два фотона), имея в запасе много гравитационной потенциальной энергии, то в энергию фотона перейдёт только масса покоя (оранжевый). Если уронить эти частицы вниз, чтобы они аннигилировали непосредственно перед ударом, у них будет больше энергии, что приведёт к появлению более синих фотонов.
Сценарий 2: частица и античастица аннигилируют в чистую энергию, а потом падают вниз до земли в виде фотонов с нулевой массой покоя. Тогда вся их энергия массы покоя превратится в энергию фотонов.
Получается, что в данном случае общая энергия этих фотонов, у каждого из которых есть энергия E = pc, должна быть равной сумме энергий масс покоя частицы и античастицы.
Теперь представим, что эти фотоны добрались до поверхности планеты, и после этого мы измеряем их энергию. По закону сохранения, их энергия должна равняться энергии фотонов из первого сценария. Значит, фотон должен набирать энергию, падая в гравитационном поле. Это явление известно, как гравитационный синий сдвиг. Кроме того, из этого следует идея о том, что масса покоя частицы должна равняться E = mc².
Когда квант излучения покидает гравитационное поле, его частота должна испытать красный сдвиг, чтобы энергия сохранилась. При падении частота должна сдвинуться в синий диапазон. Это имеет смысл, только если гравитация связана не только с массой, но и с энергией. Гравитационное красное смещение – одно из ключевых предсказаний Общей теории относительности Эйнштейна. Но его только недавно проверили в окружении с такими сильными полями, как центр нашей Галактики.
Есть только одно определение энергии, подходящее ко всем частицам, и имеющим, и не имеющим массу, и удовлетворяющее сценариям 1 и 2, которые должны выдать одинаковые результаты. E = √(m 2 c 4 + p 2 c 2 ). Посмотрим, что с ним будет в разных ситуациях.
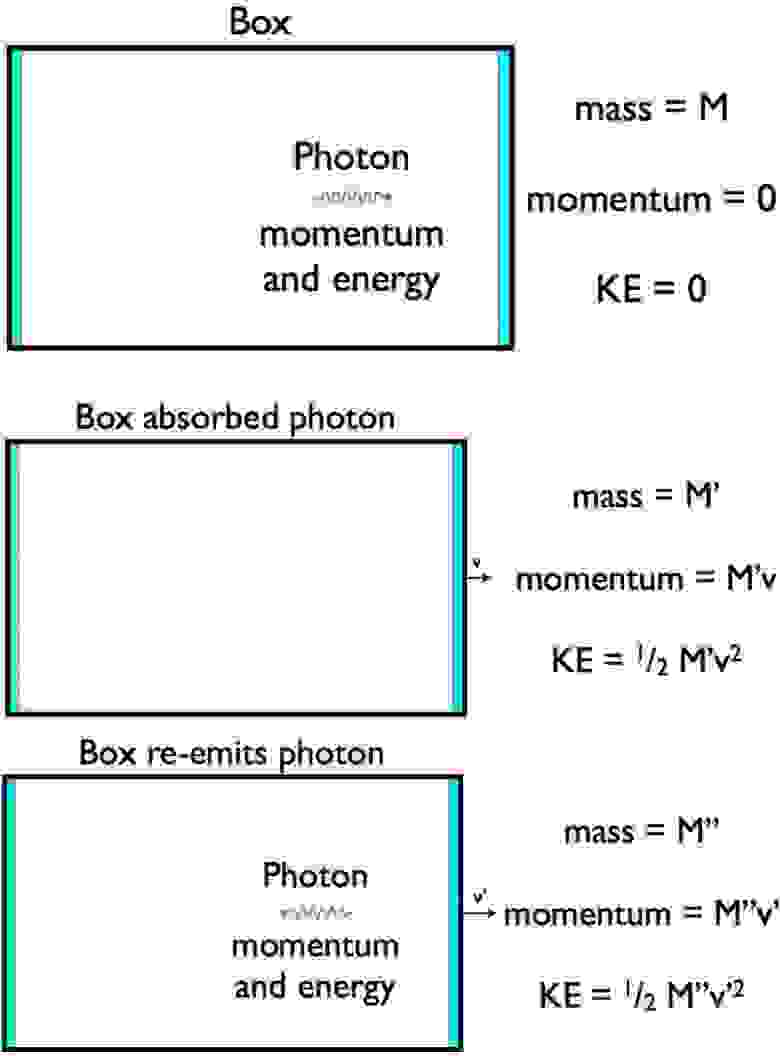
Вверху: фотон движется внутри коробки. В середине: коробка поглотила фотон. Внизу: фотон переиспущен в противоположном направлении. Из такого эксперимента, принимая законы сохранения энергии и импульса, можно вывести знаменитое E = mc².
Конечно, так выводить E = mc² не стоит, но это мой любимый способ иллюстрации этой задачи. Могу порекомендовать ещё три способа иллюстрации, а также описание того, как это сделал сам Эйнштейн. Второй моей любимой иллюстрацией вывода этой формулы будет рассмотрение фотона, движущегося в неподвижной коробке с зеркалом на одной из стенок.
Когда фотон сталкивается с зеркалом, он на некоторое время поглощается, в результате чего коробка должна приобрести немного энергии, и начать двигаться в том же направлении, что и фотон – это единственный способ сохранить энергию и импульс.
После переиспускания фотон движется в противоположном направлении, поэтому коробке (потерявшей немного массы после переиспускания фотона) нужно двигаться вперёд ещё быстрее.
И хотя тут много неизвестных, в такой ситуации можно написать множество уравнений, которым необходимо совпадать. Общая энергия всех частей системы и общий момент должны быть эквивалентными. Если решить эти уравнения, получится только одно определение энергии массы покоя: E = mc².
Эйнштейн выводит Специальную теорию относительности перед зрителями, 1934 год. Если потребовать сохранения энергии и применить теорию относительности к подходящим системам, необходимо, чтобы E = mc².
Можно представить себе совсем не такую вселенную, в которой мы живём. Возможно, там не сохраняется энергия – и тогда формула E = mc² может не быть универсальным выражением массы покоя. Возможно, мы могли бы нарушить закон сохранения импульса – тогда наше определение общей энергии, E = √(m 2 c 4 + p 2 c 2 ), не было бы верным. А если бы там не действовала Общая теория относительности, или импульс и энергия фотона не были бы связаны соотношением E = pc, тогда E = mc² не была бы универсальной формулой для массивных частиц.
Но в нашей Вселенной энергия сохраняется, и работает Общая теория относительности. Поэтому нужно просто подобрать подходящие условия эксперимента. И даже не проводя его на самом деле, можно прийти только к одному непротиворечивому значению для энергии массы покоя частицы. Можно представить себе вселенную, в которой взаимоотношение массы и энергии были бы другими, но она была бы совсем непохожей на нашу. И это не просто удобное определение – это единственный способ сохранить энергию и импульс с имеющимися у нас законами физики.