единицы ацп что такое
Аналого-цифровые преобразователи (АЦП). Основные типы и их параметры.
АЦП – устройство, преобразующее значение непрерывной аналоговой величины в эквивалентный ей цифровой код.
В полупроводниковых АЦП наибольшее распространение получили три известных принципа преобразования:
· последовательного счета;
· поразрядного кодирования (последовательного приближения);
· параллельного преобразования.
АЦП последовательного счета
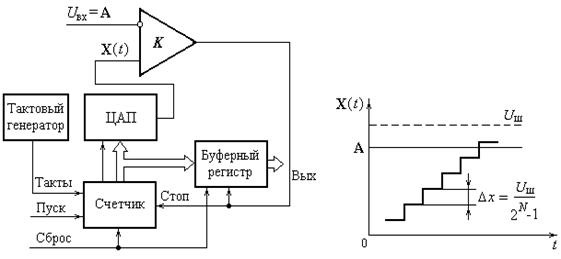
Простейший АЦП данного типа и его временная диаграмма (для случая Uвх = Α = const) представлены на рисунке.
АЦП состоит из компаратора, ЦАП, двоичного счетчика, выходного буферного регистра. После команд СБРОС и ПУСК, подаваемых на АЦП, импульсы тактового генератора начинают увеличивать показания счетчика, а, следовательно, и выходной сигнал ЦАП Χ(t) ступеньками по Δx. Компаратор определяет разницу между Χ и Α. Если окажется, что Χ – Α > 0, компаратор вырабатывает сигнал СТОП, счетчик останавливается и индицирует двоичный код, эквивалентный входному сигналу Uвх = Α. Общее время преобразования сигнала зависит от его величины.
Недостатком такой схемы АЦП является ее низкое быстродействие.
АЦП последовательного приближения
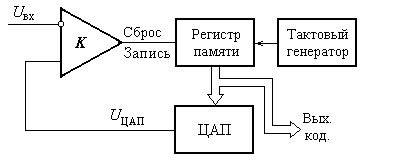
Упрощенная схема АЦП последовательного приближения приведена на рисунке
После пуска схемы первым тактовым импульсом регистр памяти (РП) устанавливает старший разряд ЦАП в единицу. При этом, если Uвх > UЦАП, то компаратор подтверждает состояние РП и ЦАП. Следующим тактовым импульсом единица устанавливается в следующем за старшим разряде. Если окажется, что Uвх
Статические параметры АЦП во многом по смыслу аналогичны статическим параметрам ЦАП и рассмотрены тут — www.drive2.ru/b/2558751/
Среди динамических параметров АЦП основными являются:
максимальная частота преобразования – частота дискретизации входного сигнала;
апертурное время – время, в течение которого сохраняется неопределенность между значением выборки и временем, к которому оно относится;
апертурная неопределенность – случайное изменение апертурного времени в конкретной точке характеристики преобразования;
время кодирования – время, в течение которого осуществляется непосредственное преобразование установившегося значения входного сигнала (время от начала импульса запуска до появления выходного кода).
Что такое АЦП
АЦП применяется в цифровой технике. В частности, почти все современные микроконтроллеры имеют встроенный АЦП.
Как вы уже наверняка знаете, микропроцессоры (как и компьютерные процессоры) не понимают ничего, кроме двоичных чисел. Из этого следует, что микропроцессор (который является основой любого микроконтроллера) не может напрямую обработать аналоговый сигнал.
Для того, чтобы объяснить это микропроцессору, который, как мы помним, понимает только двоичные числа, используется АЦП, который, как я уже сказал, преобразует аналоговый сигнал в двоичный код. Далее в общих чертах рассмотрим работу АЦП.
Принцип работы АЦП
Итак, мы узнали, что АЦП преобразует аналоговый сигнал в цифровой. Но как он это делает?
Итак, первым делом АЦП должен преобразовать аналоговый сигнал в дискретный. Для чего это нужно?
А как же, например, напряжение 4,3 В? Да никак. Оно просто округляется, и АЦП преобразует его в число 4. Этот простой пример отображён на рисунке ниже.
Расскажу и об этом, но сначала о разрядности АЦП.
Разрядность АЦП
Это значит, что измеряемый диапазон (сигнал на входе АЦП или на аналоговом входе микроконтроллера) мы можем разбить на 256 значений. Таким образом мы можем определить точность измеряемого значения, которую может обеспечить данный АЦП. Сделать это можно по формуле:
Например, если у нас 8-разрядный АЦП, и мы хотим измерять напряжение в диапазоне 0. 255В, то точность измерений будет:
256 / 2 8 = 256 / 256 = 1 В
Если же мы хотим измерять напряжение с этим же АЦП в диапазоне 0. 15В, то точность измерений будет:
16 / 2 8 = 16 / 256 = 0,0625 В
Из этого следует, что для того, чтобы повысить точность, требуется либо сузить диапазон измеряемых значений, либо повысить разрядность АЦП. Например:
256 / 212 = 256 / 4096 = 0,0625 В
То есть 12-разрядный АЦП обеспечит уже довольно высокую точность даже при измерении сигналов с относительно большим диапазоном значений.
АЦП микроконтроллера обычно измеряет только напряжение в диапазоне от 0 до напряжения питания микроконтроллера.
Характеристики АЦП
Все эти характеристики описаны в документации на АЦП (если он выполнен в виде отдельной микросхемы) или в документации на микроконтроллер (если АЦП встроен в микроконтроллер).
Кроме разрядности, о которой мы уже говорили, можно назвать ещё несколько основных характеристик.
1 LSB = 1 / 2 8 = 1 / 256 = 0,004 В
Иными словами, эта характеристика определяет, насколько “кривой” может быть линия на графике выходного сигнала, которая в идеале должна быть прямой (см. рис.).
Абсолютная точность. Также измеряется в LSB. Иными словами, это погрешность измерения. Например, если эта характеристика равна +/- 2 LSB, а LSB = 0,05 В, то это означает, что погрешность измерений может достигать +/- 2*0,05 = +/- 0,1В.
Есть у АЦП и другие характеристики. Но для начала и этого более чем достаточно.
Подключение АЦП
АЦП в основном измеряют напряжение.
Попробую рассказать о том (в общих чертах), как подключить аналоговый датчик к АЦП и как потом разобраться с теми значениями, которые будет выдавать АЦП.
Если температурный датчик имеет стандартный выход, то, как правило, напряжение (или ток) на выходе датчика изменяется по линейному закону. То есть мы можем легко определить, какое напряжение будет на выходе датчика при заданной температуре.
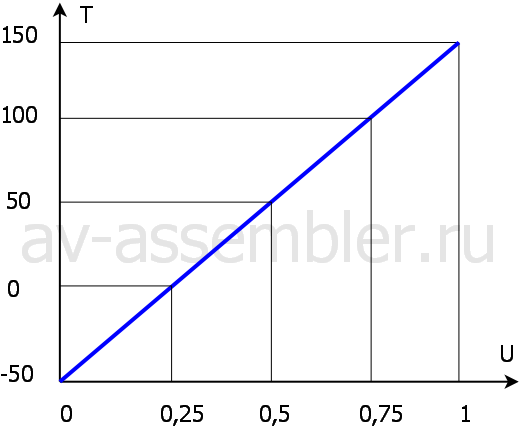
Определить напряжение по температуре визуально можно по графику (см. рис. выше). Но микроконтроллер глаз не имеет (хотя, конечно, можно поразвлекаться и создать устройство на микроконтроллере, способное распознавать образы и определять значение температуры по напряжению на графике, но оставим эти развлечения фанатам робототехники)))
То есть в шкалу от 0 до 1 нам надо впихнуть диапазон от 0 до 200 (всего 201).
Находим коэффициент преобразования:
К = U / Tд = 1 / 200 = 0,005 (1)
Теперь у нас есть все необходимые данные, чтобы в программе микроконтроллера преобразовать значение на выходе АЦП в значение температуры.
Мы помним, что мы сместили диапазон температур на 50 градусов. Это надо учитывать при преобразовании значения на выходе АЦП в температуру.
А формула будет такая:
Например, если на выходе АЦП 0,5 В, то
Теперь нам надо определить дискретность, то есть желаемую точность измерений.
Как вы помните, абсолютная погрешность может составлять несколько LSB. К тому же ещё существуют нелинейные искажения, которые обычно равны 0,5 LSB. То есть общая погрешность АЦП может доходить до 2-3 LSB.
В нашем случае это:
Uп = 3 LSB * 0,005 = 0,015 В
Если в вашем случае не так всё гладко, то снова используем формулу, выведенную из (1):
Тд = Uп / K = 0,015 / 0,005 = 3
Если погрешность в 3 градуса вас устраивает, то можно ничего не менять. Ну а если нет, то придётся подобрать АЦП с большей разрядностью либо подыскать другой датчик (с другим температурным диапазоном или с другим выходным напряжением).
Тогда абсолютная погрешность будет:
Тд = Uп / K = 0,015 / 0,01 = 1,5 градуса.
Это уже более-менее приемлемо. Ну а если у вас будет датчик с выходом 0. 5В (это тоже стандартный сигнал), то
А абсолютная погрешность будет:
Тд = Uп / K = 0,015 / 0,05 = 0,3 градуса.
Это уже вообще ништяк.
Но! Не забывайте, что здесь мы рассматриваем только погрешность АЦП. Но и у самого датчика тоже есть погрешность, которую также надо учитывать.
Но всё это уже из области электроники и метрологии, поэтому данную статью я здесь и закончу.
А в конце на всякий случай приведу формулу обратного преобразования температуры в напряжение:
Национальная библиотека им. Н. Э. Баумана
Bauman National Library
Персональные инструменты
АЦП (Аналого-цифровой преобразователь)
Аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC).
Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.
Содержание
Разрешение
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП — связано с его разрядностью. В случае единичного измерения без учёта шумов разрешение напрямую определяется разрядностью АЦП.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП измеряется в битах, в троичных АЦП измеряется в тритах. Например, двоичный АЦП, способный выдать 256 дискретных значений (0…255), имеет разрядность 8 бит, поскольку 2 8 = 256, троичный АЦП, имеющий разрядность 8 трит, способен выдать 6 561 дискретное значение, поскольку 3 8 = 6561.
Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений. Например:
На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (effective number of bits — ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. Для достижения заявленной разрядности отношение С/Ш входного сигнала должно быть примерно 6 дБ на каждый бит разрядности.
Типы преобразования
Линейные АЦП
Большинство АЦП считаются линейными, хотя аналого-цифровое преобразование по сути является нелинейным процессом (поскольку операция отображения непрерывного пространства в дискретное — операция нелинейная). Термин линейный применительно к АЦП означает, что диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением, то есть выходное значение k достигается при диапазоне входных значений от
Константа b, как правило, имеет значение 0 или −0.5. Если b = 0, АЦП называют квантователь с ненулевой ступенью (mid-rise), если же b = −0,5, то АЦП называют квантователь с нулём в центре шага квантования (mid-tread).
Нелинейные АЦП
Если бы плотность вероятности амплитуды входного сигнала имела равномерное распределение, то отношение сигнал/шум (применительно к шуму квантования) было бы максимально возможным. По этой причине обычно перед квантованием по амплитуде сигнал пропускают через безынерционный преобразователь, передаточная функция которого повторяет функцию распределения самого сигнала. Это улучшает достоверность передачи сигнала, так как наиболее важные области амплитуды сигнала квантуются с лучшим разрешением. Соответственно, при цифро-аналоговом преобразовании потребуется обработать сигнал функцией, обратной функции распределения исходного сигнала.
Это тот же принцип, что и используемый в компандерах, применяемых в магнитофонах и различных коммуникационных системах, он направлен на максимизацию энтропии. (Не путать компандер с компрессором!)
Например, голосовой сигнал имеет лапласово распределение амплитуды. Это означает, что окрестность нуля по амплитуде несёт больше информации, чем области с большей амплитудой. По этой причине логарифмические АЦП часто применяются в системах передачи голоса для увеличения динамического диапазона передаваемых значений без изменения качества передачи сигнала в области малых амплитуд.
8-битные логарифмические АЦП с a-законом или μ-законом обеспечивают широкий динамический диапазон и имеют высокое разрешение в наиболее критичном диапазоне малых амплитуд; линейный АЦП с подобным качеством передачи должен был бы иметь разрядность около 12 бит.
Основные типы архитектуры АЦП
Существует несколько основных типов архитектуры АЦП, хотя в пределах каждого типа существует также множество вариаций. Различные типы измерительного оборудования используют различные типы АЦП. Например, в цифровом осциллографе используется высокая частота дискретизации, но не требуется высокое разрешение. В цифровых мультиметрах нужно большее разрешение, но можно пожертвовать скоростью измерения. Системы сбора данных общего назначения по скорости дискретизации и разрешающей способности обычно занимают место между осциллографами и цифровыми мультиметрами. В оборудовании такого типа используются АЦП последовательного приближения либо сигма-дельта АЦП. Существуют также параллельные АЦП для приложений, требующих скоростной обработки аналоговых сигналов, и интегрирующие АЦП с высокими разрешением и помехоподавлением.
На рис.1. показаны возможности основных архитектур АЦП в зависимости от разрешения и частоты дискретизации.
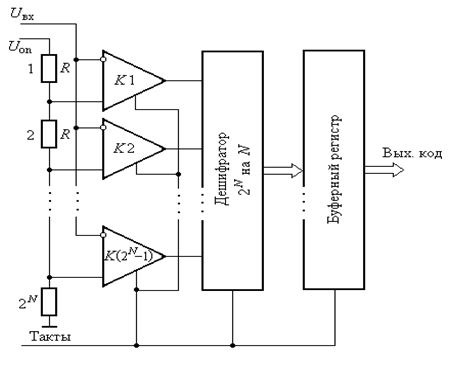
Параллельные АЦП
Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5Г (5х10 9 ) отсчетов/сек для стандартных устройств и 20Г отсчетов/сек для оригинальных разработок. Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10-ти разрядные версии.
АЦП последовательного приближения
Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 100К (1х10 3 ) до 1М (1х10 6 ) отсчетов/сек.
Рис. 3 показывает упрощенную блок-схему АЦП последовательного приближения. В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0, за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением.
Например, для 8-разрядного АЦП последовательного приближения (рис. 4) выходы регистра при этом устанавливаются в «10000000». Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0. Это дает регистру последовательного приближения команду переключить свои выходы в состояние «01000000», что соответственно приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в «0», то выходы регистра переключились бы в состояние «00100000». Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение (рис. 4), и компаратор переключается в состояние логической 1. Это предписывает регистру последовательного приближения сохранить «1» во втором разряде и подать «1» на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования.
Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП. Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа.
Сигма-дельта АЦП
Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100К отсчетов/сек, а при 24 разрядах эта частота падает до 1К отсчетов/сек и менее, в зависимости от устройства.
Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов.
Принцип работы сигма-дельта АЦП сложнее для понимания. Эта архитектура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8М отсчетов/сек.
Блок-схема сигма-дельта АЦП первого порядка приведена на рис. 5. Аналоговый сигнал подается на интегратор, выходы которого подсоединены к компаратору, который в свою очередь присоединен к 1-разрядному ЦАП в петле обратной связи. Путем серии последовательных итераций интегратор, компаратор, ЦАП и сумматор дают поток последовательных битов, в котором содержится информация о величине входного напряжения.
Так как внутренний цифровой ФНЧ в сигма-дельта АЦП представляет собой неотъемлемую часть для осуществления процесса преобразования, время установления ФНЧ становится фактором, который необходимо учитывать при скачкообразном изменении входного сигнала. Например, при переключении входного мультиплексора или при переключении предела измерения прибора необходимо подождать, пока пройдут несколько отсчетов АЦП, и лишь потом считывать корректные выходные данные.
Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП.
Интегрирующие АЦП
На рисунке 6 показан принцип работы АЦП двухтактного интегрирования. Входной сигнал заряжает конденсатор в течение фиксированного периода времени, который обычно составляет один период частоты питающей сети (50 или 60Гц) или кратен ему. При интегрировании входного сигнала в течение промежутка времени такой длительности высокочастотные помехи подавляются. Одновременно исключается влияние нестабильности напряжения сетевого источника питания на точность преобразования. Это происходит потому, что значение интеграла от синусоидального сигнала равно нулю, если интегрирование осуществляется во временном интервале, кратном периоду изменения синусоиды.
По окончании времени заряда АЦП разряжает конденсатор с фиксированной скоростью, в то время как внутренний счетчик подсчитывает количество тактовых импульсов за время разряда конденсатора. Большее время разряда, таким образом, соответствует большему значению показаний счетчика и большему измеряемому напряжению (рис. 6).
Точность
Имеется несколько источников погрешности АЦП. Ошибки квантования и (считая, что АЦП должен быть линейным) нелинейности присущи любому аналого-цифровому преобразованию. Кроме того, существуют так называемые апертурные ошибки, которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта).
Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд. В приведённом выше примере 8-битного двоичного АЦП ошибка в 1 МЗР составляет 1/256 от полного диапазона сигнала, то есть 0,4 %, в 8-тритном троичном АЦП ошибка в 1 МЗР составляет 1/6561, то есть 0,015 %.
Ошибки квантования
Ошибки квантования являются следствием ограниченного разрешения АЦП. Этот недостаток не может быть устранён ни при каком типе аналого-цифрового преобразования. Абсолютная величина ошибки квантования при каждом отсчёте находится в пределах от нуля до половины МЗР.
Нелинейность
Всем АЦП присущи ошибки, связанные с нелинейностью, которые являются следствием физического несовершенства АЦП. Это приводит к тому, что передаточная характеристика (в указанном выше смысле) отличается от линейной (точнее от желаемой функции, так как она не обязательно линейна). Ошибки могут быть уменьшены путём калибровки.
Важным параметром, описывающим нелинейность, является интегральная нелинейность (INL) и дифференциальная нелинейность (DNL).
Апертурная погрешность (джиттер)
Легко видеть, что ошибка относительно невелика на низких частотах, однако на больших частотах она может существенно возрасти.
Эффект апертурной погрешности может быть проигнорирован, если её величина сравнительно невелика по сравнению с ошибкой квантования. Таким образом, можно установить следующие требования к дрожанию фронта сигнала синхронизации:
Из этой таблицы можно сделать вывод о целесообразности применения АЦП определённой разрядности с учётом ограничений, накладываемых дрожанием фронта синхронизации (clock jitter). Например, бессмысленно использовать прецизионный 24-битный АЦП для записи звука, если система распределения синхросигнала не в состоянии обеспечить ультрамалой неопределённости.
Частота дискретизации
Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала. Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП.
Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации) и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции. Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова точное восстановление возможно только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала.
Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным по крайней мере от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения — УВХ. УВХ, как правило, хранит входное напряжение в конденсаторе, который соединён со входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение. Многие АЦП, выполненные в виде интегральных микросхем содержат встроенное УВХ.
Наложение спектров (алиасинг)
Все АЦП работают путём выборки входных значений через фиксированные интервалы времени. Следовательно, выходные значения являются неполной картиной того, что подаётся на вход. Глядя на выходные значения, нет никакой возможности установить, как вёл себя входной сигнал между выборками. Если известно, что входной сигнал меняется достаточно медленно относительно частоты дискретизации, то можно предположить, что промежуточные значения между выборками находятся где-то между значениями этих выборок. Если же входной сигнал меняется быстро, то никаких предположений о промежуточных значениях входного сигнала сделать нельзя, а следовательно, невозможно однозначно восстановить форму исходного сигнала.
Если последовательность цифровых значений, выдаваемая АЦП, где-либо преобразуется обратно в аналоговую форму цифро-аналоговым преобразователем, желательно, чтобы полученный аналоговый сигнал был максимально точной копией исходного сигнала. Если входной сигнал меняется быстрее, чем делаются его отсчёты, то точное восстановление сигнала невозможно, и на выходе ЦАП будет присутствовать ложный сигнал. Ложные частотные компоненты сигнала (отсутствующие в спектре исходного сигнала) получили название alias (ложная частота, побочная низкочастотная составляющая). Частота ложных компонент зависит от разницы между частотой сигнала и частотой дискретизации. Например, синусоидальный сигнал с частотой 2 кГц, дискретизованный с частотой 1.5 кГц был бы воспроизведён как синусоида с частотой 500 Гц. Эта проблема получила название наложение частот (aliasing).
Для предотвращения наложения спектров сигнал, подаваемый на вход АЦП, должен быть пропущен через фильтр нижних частот для подавления спектральных компонент, частота которых превышает половину частоты дискретизации. Этот фильтр получил название anti-aliasing (антиалиасинговый) фильтр, его применение чрезвычайно важно при построении реальных АЦП.
Хотя наложение спектров в большинстве случаев является нежелательным эффектом, его можно использовать во благо. Например, благодаря этому эффекту можно обойтись без преобразования частоты вниз при оцифровке узкополосного высокочастотного сигнала (смотри смеситель). Для этого, однако, входные аналоговые каскады АЦП должны иметь значительно более высокие параметры, чем это требуется для стандартного использования АЦП на основной (видео или низшей) гармонике.
Подмешивание псевдослучайного сигнала (dither)
Некоторые характеристики АЦП могут быть улучшены путём использования методики подмешивания псевдослучайного сигнала (англ. dither). Она заключается в добавлении к входному аналоговому сигналу случайного шума (белый шум) небольшой амплитуды. Амплитуда шума, как правило, выбирается на уровне половины МЗР. Эффект от такого добавления заключается в том, что состояние МЗР случайным образом переходит между состояниями 0 и 1 при очень малом входном сигнале (без добавления шума МЗР был бы в состоянии 0 или 1 долговременно). Для сигнала с подмешанным шумом вместо простого округления сигнала до ближайшего разряда происходит случайное округление вверх или вниз, причём среднее время, в течение которого сигнал округлён к тому или иному уровню зависит от того, насколько сигнал близок к этому уровню. Таким образом, оцифрованный сигнал содержит информацию об амплитуде сигнала с разрешающей способностью лучше, чем МЗР, то есть происходит увеличение эффективной разрядности АЦП. Негативной стороной методики является увеличение шума в выходном сигнале. Фактически, ошибка квантования размазывается по нескольким соседним отсчётам. Такой подход является более желательным, чем простое округление до ближайшего дискретного уровня. В результате использования методики подмешивания псевдослучайного сигнала мы имеем более точное воспроизведение сигнала во времени. Малые изменения сигнала могут быть восстановлены из псевдослучайных скачков МЗР путём фильтрации. Кроме того, если шум детерминирован (амплитуда добавляемого шума точно известна в любой момент времени), то его можно вычесть из оцифрованного сигнала, предварительно увеличив его разрядность, тем самым почти полностью избавиться от добавленного шума.
Звуковые сигналы очень малых амплитуд, оцифрованные без псевдослучайного сигнала, воспринимаются на слух очень искажёнными и неприятными. При подмешивании псевдослучайного сигнала истинный уровень сигнала представлен средним значением нескольких последовательных отсчётов.
Однако, в последнее время, в связи с удешевлением 24-битных АЦП, имеющих даже без dihter’а динамический диапазон более 120 дБ, что на несколько порядков превышает полный воспринимаемый человеком диапазон слуха, данная технология потеряла актуальность в звукотехнике. При этом, она используется в ВЧ и СВЧ технике, где битность АЦП обычно мала из-за высокой частоты дискретизации.
Очень похожий процесс, также называемый dither или диффузия ошибок, применяется для представления полутонов изображений в компьютерной графике при малом количестве бит на пиксел. При этом изображение становится зашумленным, но визуально воспринимается реалистичнее чем то же изображение полученное простым квантованием.
Передискретизация
Как правило, сигналы оцифровываются с минимально необходимой частотой дискретизации из соображений экономии, при этом шум квантования является белым, то есть его спектральная плотность мощности равномерно распределена во всей полосе. Если же оцифровать сигнал с частотой дискретизации, гораздо большей, чем по теореме Котельникова-Шеннона, а затем подвергнуть цифровой фильтрации для подавления спектра вне частотной полосы исходного сигнала, то отношение сигнал/шум, будет лучше, чем при использовании всей полосы. Таким образом можно достичь эффективного разрешения большего, чем разрядность АЦП.
Передискретизация также может быть использована для смягчения требований к крутизне перехода от полосы пропускания к полосе подавления антиалиасингового фильтра. Для этого сигнал оцифровывают, например, на вдвое большей частоте, затем производят цифровую фильтрацию, подавляя частотные компоненты вне полосы исходного сигнала, и, наконец, понижают частоту дискретизации путём децимации.
Характеристики основных типов АЦП
Ниже перечислены основные способы построения и характеристики электронных АЦП более подробно:
Неэлектронные АЦП обычно строятся на тех же принципах.
Применение АЦП в звукозаписи
АЦП встроены в большую часть современной звукозаписывающей аппаратуры, поскольку обработка звука делается, как правило, на компьютерах; даже при использовании аналоговой записи АЦП необходим для перевода сигнала в PCM-поток, который будет записан на компакт-диск.
Современные АЦП, используемые в звукозаписи, могут работать на частотах дискретизации до 192 кГц. Многие люди, занятые в этой области, считают, что данный показатель избыточен и используется из чисто маркетинговых соображений (об этом свидетельствует теорема Котельникова-Шеннона). Можно сказать, что звуковой аналоговый сигнал не содержит столько информации, сколько может быть сохранено в цифровом сигнале при такой высокой частоте дискретизации, и зачастую для Hi-Fi-аудиотехники используется частота дискретизации 44,1 кГц (стандартная для компакт-дисков) или 48 кГц (типична для представления звука в компьютерах). Однако широкая полоса упрощает и удешевляет реализацию антиалиасинговых фильтров, позволяя делать их с меньшим числом звеньев или с меньшей крутизной в полосе заграждения, что положительно сказывается на фазовой характеристике фильтра в полосе пропускания.
Аналого-цифровые преобразователи для звукозаписи имеют широкий диапазон цен — от 100 до 10 тыс. долл. и выше за двухканальный АЦП.
АЦП для звукозаписи, используемые в компьютерах, бывают внутренние и внешние. Также существует свободный программный комплекс PulseAudio для Linux, позволяющий использовать вспомогательные компьютеры как внешние ЦАП/АЦП для основного компьютера с гарантированным временем запаздывания.
Другие применения
Аналого-цифровое преобразование используется везде, где требуется обрабатывать, хранить или передавать сигнал в цифровой форме.