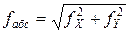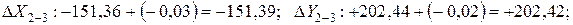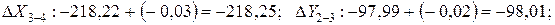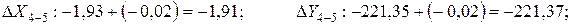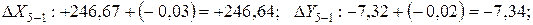если дирекционный угол больше 360 что делать
Дирекционные углы смежных линий
Дирекционные углы смежных линий изображены на рисунке:
Для линии AB смежной явлется линия BC, тогда αA-B дирекционный угол линии AB, а αB-C это дирекционный угол смежной линии BC.
Между дирекционными углами смежных линий можно установить связь, если известен угол β при общей точке B.
Угол β измеряется на местности теодолитом, причем если двигаться по направлению A-B-C, тогда угол β который окажется по левую руку считается левым (βлев), а по правую руку – правым (βпр). Двигаясь в обратном направлении (C-B-A), правый угол становится левым, а левый сответственно правым, поэтому при расчетах необходимо быть внимательным.
Зная дирекционный угол одной из линий и угол β между этими линиями, можно вычислить дирекционный угол другой линии, используя формулы:
При вычислении по этим формулам дирекционный угол смежной линии может получиться или меньше нуля (отрицательным) или превышать 360°, тогда к нему соответственно прибавляют или от него отнимают 360°.
Примеры вычисления дирекционных углов смежных линий
Пример 1: вычислить дирекционный угол смежной линии BC, если дирекционный угол линии AB равен 75°57′ и угол β = 68°14′.
двигаясь по направлению A-B-C угол β является правым, тогда используя формулу можем записать:
Пример 2: вычислить дирекционный угол смежной линии BA, если дирекционный угол линии CB равен 270°05′ и угол β = 290°14′:
двигаясь по направлению C-B-A угол β является левым, тогда используя формулу можем записать:
дирекционный угол получился больше 360°, поэтому из его значения отнимаем 360°
Вычисление дирекционных углов
По известному дирекционному углу an и по исправленным горизонтальным углам bиспр вычисляются дирекционные углы остальных сторон теодолитного хода по формулам для правых горизонтальных углов:
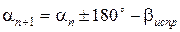
Величина дирекционного угла не может превышать 360° и быть меньше 0°. Если величина дирекционного угла больше 360°, то из результата вычислений необходимо вычесть 360° (см. пример).
Контроль вычисления дирекционных углов. В замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.
Пример вычисления дирекционных углов:
Дирекционный угол исходной стороны a1-2 равен 45°45¢.
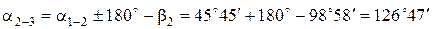
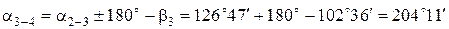
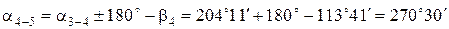
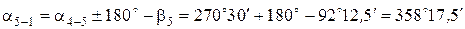
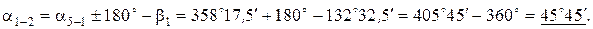
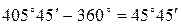
Контроль вычисления дирекционных углов получился.
Все результаты вычислений заносятся в таблицу «Ведомость вычисления координат» (табл. 2).
1.3 Вычисление приращений координат
Вычисление приращений координат выполняется по формулам:
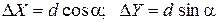
где d – горизонтальное проложение (длина) линии; a – дирекционный угол этой линии.
Приращения координат вычисляются с точностью два знака после запятой.
Пример вычисления приращений координат:
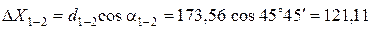
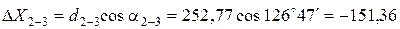
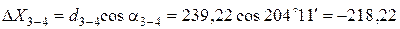
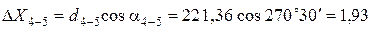
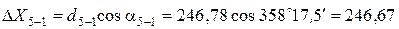
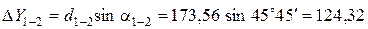
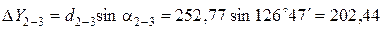
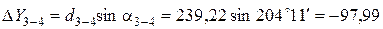
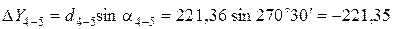
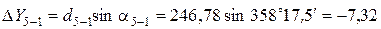
Все результаты вычисления заносятся в табл. 2. Пример вычисления тригонометрических функций на калькуляторе приведен в отдельном файле.
1.4 Уравнивание линейных измерений
Разность между суммой вычисленных приращений координат и теоретической суммой называется линейной невязкой хода и обозначается fХ и fY. Уравнивание линейных измерений выполняется по осям Х и Y.
Линейная невязка вычисляется по формулам:
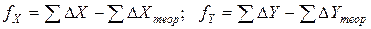
Теоретическая сумма приращений координат зависит от геометрии хода. В замкнутом теодолитном ходе она равна нулю, тогда невязка равна
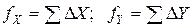
Прежде, чем распределять невязки в приращения координат, необходимо убедиться в их допустимости. Для чего вычисляется абсолютная невязка хода fабс
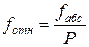
где Р – периметр хода (сумма длин сторон), м.
Относительная невязка сравнивается с допустимой 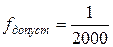
В случае, когда полученная относительная невязка допустима, т.е. 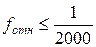
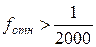
Поправки в приращения координат dX и dY вычисляются по формулам с округлением до 0,01 м:
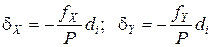
где dX и dY – поправка в приращение по оси Х и Y, соответственно, м; fX и fY – невязки по осям, м; Р – периметр (сумма сторон), м; di – измеренная длина (горизонтальное проложение), м.
Знак у поправки противоположен знаку невязки. Поправки записываются в «Ведомость вычисления координат». В примере (табл. 6) поправки показаны красным цветом.
После вычисления поправок следует сделать проверку, т.е. сложить все поправки. Если их сумма будет равна невязке с обратным знаком, то распределение невязки выполнено правильно. То есть:
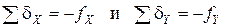
Вычисляются исправленные приращения.
Полученные поправки алгебраически прибавляются к соответствующим приращениям и получаются исправленные приращения:
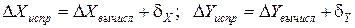
Контроль: сумма исправленных приращений в замкнутом теодолитном ходе должна равняться нулю, т.е. должно выполняться равенство:
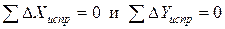
Пример вычисления линейной невязки:
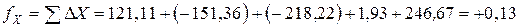
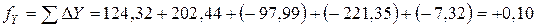
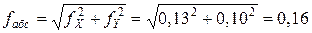
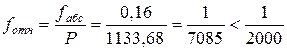
Пример вычисления поправок в приращения координат:
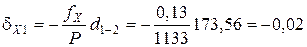
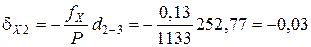
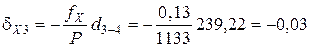
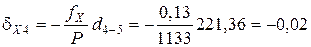
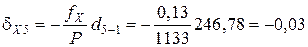
Контроль 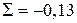
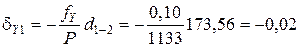
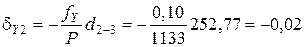
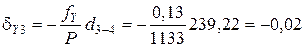
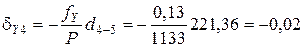
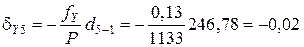
Контроль 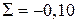
Поправки записываются в «Ведомость вычисления координат» над вычисленными приращениями. В примере поправки показаны красным цветом (Табл. 2).
Пример вычисления исправленных приращений координат:
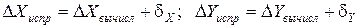
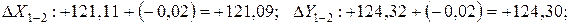
Контроль 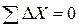
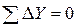
Сумма исправленных приращений равна нулю, т.е. контроль выполняется.
Координаты точек теодолитного хода: последовательность вычислений
Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.
На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.
Общие понятия о системах координат в геодезии
Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.
Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.
В геодезии координатные системы разделены на следующие две группы:
Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.
Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.
Исходные данные для расчетов
Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.
По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:
– горизонтальные углы пунктов;
– измеренное расстояние между ними;
– координаты пункта ГГС или опорной сети;
– значение исходного дирекционного угла.
Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.
Уравнивание измерений
Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:
\(\sum \beta _<изм>=\beta _<1>+\beta _<2>+…\beta _
\(\sum \beta _<теор>\) – теоретическая сумма, определяемая выражением:
\(n\) – количество углов.
Вычисленная невязка допустима, если соответствует требованию:
Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:
Правильность уравнивания подтверждается следующим условием:
Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:
Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.
Вычисление дирекционных углов вершин
В геодезии за дирекционный угол (\(\alpha \)) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:
Для левой стороны это выражение будет иметь такой вид:
\(\alpha _
\(\beta _<пр.исп.>\) – значение правого исправленного угла между сторонами отрезка, а \(\beta _<лев.исп.>\)– левой стороны.
Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.
После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.
| Четверть румба | Название четверти | Пределы изменения α | Формула румба | Знаки приращения | |
| ΔХ | ΔУ | ||||
| I | С.В. (северо-восток) | 0° – 90° | r = α | + | + |
| II | Ю.В. (юго-восток) | 90°-180° | r = 180° – α | – | + |
| III | Ю.З. (юго-запад) | 180°-270° | r = α – 180° | – | – |
| IV | С.З. (северо-запад) | 270°-360° | r = 360° – °α | + | – |
Таблица 1. Связь дирекционного угла и румба
Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.
Решение прямой и обратной геодезической задачи
Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:
\(\Delta X=d\cdot cos \alpha \)
\(\Delta Y=d\cdot sin \alpha \)
\(d\)–расстояния между соседними пунктами.
\(\alpha \) – значение дирекционного угла.
Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:
Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:
определяется румб линии \(r_<1-2>\):
из этого выходит, что:
По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:
Приращение координат и их увязка
Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:
\(\Delta X=d\cdot cos \alpha \)
\(\Delta Y=d\cdot sin \alpha \)
Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:
\(f_
\(f_
\(\sum \Delta X_<выч>,\sum \Delta Y_<выч>\) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;
\(\sum \Delta X_<теор>,\sum \Delta Y_<теор>\) – теоретические суммы приращений.
Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.
P – периметр хода, полученный суммированием всех его сторон.
Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению \(|f_<отн>|\leq |f_<доп>|\) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:
\(\delta _
Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.
Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.
\(f_
\(f_
Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.
Как вычислить координаты точек хода
Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.
Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:
\(X_
В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.
Нанесение точек на план и его оформление
После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:
\(x_
\(x_
Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.