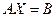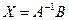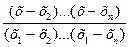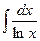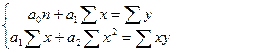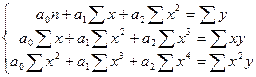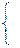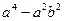если h шаг интегрирования то чем больше h тем
Тестовые вопросы по численному интегрированию.
1. Вычисление интеграла равносильно вычислению
a) объёма любой фигуры;
b) площади любой фигуры;
c) объёма тела, полученного вращением криволинейной трапеции, у которой x = а, x = b, y = 0, y = f(x);
d) площади криволинейной трапеции, ограниченной линиями x = а, x = b, y = 0, y = f(x).
2. Формула численного интегрирования метода «левых» прямоугольников имеет вид:
3. Сущность метода Симпсона заключается в том, что через три последовательные ординаты разбиения проводится
a) квадратичная парабола;
b) любая кривая;
c) синусоида;
d) гипербола.
4. Методы численного интегрирования для вычисления применимы тогда, когда
a) невозможно определить первообразную F(x);
b) невозможно определить производную f(x);
c) неизвестен интервал интегрирования [а,b];
d) функция y = f(x) задана графически.
5. Наиболее грубым методом численного интегрирования является метод
a) прямоугольников;
b) трапеций;
c) парабол;
d) Симпсона.
6. Формула численного интегрирования метода трапеций имеет вид:
7. Вычислить интеграл по методу «левых» прямоугольников с точностью =0,1
a) 4,10
b) 2,05
c) 1,34
d) 2,84
8. Необходимым условием применения формул Симпсона является: число точек разбиения должно быть
a) четным числом;
b) целым числом;
c) нечетным числом;
d) кратным «4».
9. Формула численного интегрирования метода Симпсона имеет вид
11. Известно, что интегрируемая функция – линейная, область интегрирования [-1, 1], требуемая точность не менее 0,01, интегрирование производится методом трапеций. Какое минимальное количество шагов необходимо для достижения заданной точности?
a) 1
b) 200
c) 100
d) 400
12. Заранее известно, что функция описывается полиномом второй степени (квадратным уравнением). Укажите метод (из числа рассмотренных), который позволит вычислить определенный интеграл без погрешности (погрешность округления не учитывать).
a) метод Симпсона;
b) метод трапеций;
c) метод «левых» прямоугольников;
d) метод «средних» прямоугольников.
1. Вычисление интеграла равносильно вычислению
a) объёма любой фигуры;
b) площади любой фигуры;
c) объёма тела, полученного вращением криволинейной трапеции, у которой x = а, x = b, y = 0, y = f(x);
d) площади криволинейной трапеции, ограниченной линиями x = а, x = b, y = 0, y = f(x).
2. Формула численного интегрирования метода «левых» прямоугольников имеет вид:
3. Сущность метода Симпсона заключается в том, что через три последовательные ординаты разбиения проводится
a) квадратичная парабола;
b) любая кривая;
c) синусоида;
d) гипербола.
4. Методы численного интегрирования для вычисления применимы тогда, когда
a) невозможно определить первообразную F(x);
b) невозможно определить производную f(x);
c) неизвестен интервал интегрирования [а,b];
d) функция y = f(x) задана графически.
5. Наиболее грубым методом численного интегрирования является метод
a) прямоугольников;
b) трапеций;
c) парабол;
d) Симпсона.
6. Формула численного интегрирования метода трапеций имеет вид:
7. Вычислить интеграл по методу «левых» прямоугольников с точностью =0,1
a) 4,10
b) 2,05
c) 1,34
d) 2,84
8. Необходимым условием применения формул Симпсона является: число точек разбиения должно быть
a) четным числом;
b) целым числом;
c) нечетным числом;
d) кратным «4».
9. Формула численного интегрирования метода Симпсона имеет вид
11. Известно, что интегрируемая функция – линейная, область интегрирования [-1, 1], требуемая точность не менее 0,01, интегрирование производится методом трапеций. Какое минимальное количество шагов необходимо для достижения заданной точности?
a) 1
b) 200
c) 100
d) 400
12. Заранее известно, что функция описывается полиномом второй степени (квадратным уравнением). Укажите метод (из числа рассмотренных), который позволит вычислить определенный интеграл без погрешности (погрешность округления не учитывать).
a) метод Симпсона;
b) метод трапеций;
c) метод «левых» прямоугольников;
d) метод «средних» прямоугольников.
Модуль 3. Численное интегрирование. Решение систем линейных алгебраических уравнений (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
d) 
.
3. Сущность метода Симпсона заключается в том, что через три последовательные ординаты разбиения проводится
a) квадратичная парабола;
4. Методы численного интегрирования для вычисления 
применимы тогда, когда
a) невозможно определить первообразную F(x);
b) невозможно определить производную f(x);
c) неизвестен интервал интегрирования [а, b];
d) функция y = f(x) задана графически.
5. Наиболее грубым методом численного интегрирования является метод
6. Формула численного интегрирования метода трапеций имеет вид: 
a) 
b) 
c) 
d) 
7. Вычислить интеграл 
по методу «левых» прямоугольников с точностью 
=0,1
8. Необходимым условием применения формул Симпсона является: число точек разбиения должно быть
9. Формула численного интегрирования метода Симпсона имеет вид
a) 
;
b) 
;
c) 
;
d) 
.
a) точнее получатся приближенное значение интеграла;
b) выше погрешность вычислений приближенного значение интеграла;
c) больше объем вычислений;
d) больше число точек разбиения.
11. Известно, что интегрируемая функция – линейная, область интегрирования [-1, 1], требуемая точность не менее 0,01, интегрирование производится методом трапеций. Какое минимальное количество шагов необходимо для достижения заданной точности?
12. Заранее известно, что функция описывается полиномом второй степени (квадратным уравнением). Укажите метод (из числа рассмотренных), который позволит вычислить определенный интеграл без погрешности (погрешность округления не учитывать).
c) метод «левых» прямоугольников;
d) метод «средних» прямоугольников.
2. Решение систем линейных алгебраических уравнений.
2.1. Системы линейных алгебраических уравнений (СЛАУ): понятие, определения.
Системы линейных алгебраических уравнений (далее – СЛАУ) используются во многих областях прикладной математики.
В общем виде система m линейных уравнений с n неизвестными записывается так:
Уравнения системы считаются пронумерованными: первое, второе, …, m-ое. Числа 
называются неизвестными системы; 
— коэффициентами при неизвестных системы.
Коэффициент при неизвестном 
в i-ом уравнении обозначается через 
.
Например, коэффициент a23 находится во втором уравнении системы при неизвестном x3.
Числа 
называются свободными членами системы.
Решением СЛАУ (1) называется любая совокупность чисел 
, которая, при подстановке на место неизвестных в уравнения данной системы, обращает все эти уравнения в тождества.
СЛАУ (1) называется совместной, если она имеет решение. Если СЛАУ не имеет решения, то она называется несовместной (или противоречивой). Совместная СЛАУ может иметь одно или несколько решений и называется определенной, если имеет одно единственное решение, и неопределенной, если имеет больше одного решения.
Всюду далее будем рассматривать СЛАУ, имеющие единственное решение.
Две СЛАУ с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.
Элементарными преобразованиями СЛАУ, переводящими ее в эквивалентную СЛАУ, являются:
1) перестановка двух уравнений системы;
2) умножение обеих частей уравнения системы на любое отличное от нуля число;
3) прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.
2.2. Характеристика методов решения СЛАУ.
Все методы решения СЛАУ делятся на две группы – прямые и итерационные (повторяющиеся).
Дают решение после выполнения конечного числа операций.
Используют последовательные приближения (итерации) к искомому результату.
Достаточно универсальны, всегда дают результат, причем за конечное, заранее известное, число шагов.
Позволяют получить решение с любой заданной точностью.
Нет сведений о точности полученного решения.
При их использовании заранее неизвестно количество предстоящих итераций.
В некоторых случаях вообще не дают решения.
2.3. Прямые методы решения СЛАУ: метод Гаусса.
Рассмотрим СЛАУ (2), состоящую из n уравнений с n неизвестными:
Метод Гаусса или метод последовательного исключения неизвестных наиболее распространенный из точных (прямых) методов решения СЛАУ.
Прямой ход приводит систему (2) к эквивалентной ей системе вида (2’).
(
)
Для этого сначала первое неизвестное исключают из второго и последующих уравнений системы, затем второе неизвестное исключают из третьего и последующих уравнений и так далее. Таким образом, в последнем уравнении остается только одно неизвестное. Для реализации прямого хода используют следующие известные правила:
— любое уравнение системы можно умножить на постоянный коэффициент;
— можно сложить два любых уравнения системы и результат записать вместо одного из этих уравнений.
Переход от системы (2) к системе () возможен при выполнении следующих преобразований. Пусть 
(если это не так, то можно поменять местами два уравнения системы). Разделим все члены первого уравнения системы (2) на 
, все члены второго уравнения на 
, третьего – на 
, и так далее. Если какой-то из этих коэффициентов равен нулю, то соответствующее уравнение не преобразовывается. Затем вычтем из второго, третьего, …, n-ого уравнения соответствующие части первого, получим
от любой строки можно вычесть другую строку, умноженную на
+Решение систем линейных уравнений методом Гаусса…..
+выбираем разрешающее уравнение и ставим его на первое место;
во всех уравнениях кроме первого коэффициенты при х1 исключаем, т.е. делаем равными нулю;
из оставшихся уравнений выбираем разрешающее и ставим его на второе место;
из остальных уравнений исключаем коэффициенты при х2, т.е. делаем равными нулю и т.д.;
получим треугольную систему, из которой, поднимаясь вверх находим последовательно все хn.
+Запись системы уравнений в матричной форме….
+
+Решение систем линейных уравнений методом обратной матрицы…
+ 
+Интерполяция функции у(х) заключается в …
+нахождении значений у по значениям х, находящимися в промежутках между узлами хi
+Чем заменяется функция у(х) при интерполяции…
+интерполяционным полиномом Р(х), значения которого Р(хi) в узлах точно совпадают с у(хi)
+ Запишите многочлен Лагранжа…
+ Чему равен коэффициент Лагранжа Р1(х).
+Р1(х)= 
+ Приведите примеры «неберущихся» интегралов……
+ 
; 
; 
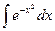
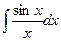
+ Как вычисляют «неберущиеся» интегралы? ……
+ Наиболее часто применяются следующие методы численного
+метод трапеции, метод Симпсона
+ Что такое эмпирическая формула.
+зависимость, найденная опытным путем и выраженная в виде формулы
+ Из каких этапов состоит построение эмпирической формулы.
+выбор вида функции и определение параметров выбранной функции
+ На основе чего устанавливается вид эмпирической функции у=f(x).
+на основе логического анализа
+ Методом наименьших квадратов определяются…
+параметры эмпирической формулы
+ Принцип метода наименьших квадратов……
+из формул вида у= f(x) наиболее соответствующей опытным данным считается та, для которой сумма квадратов отклонений опытных данных от расчетных является минимальной
+ Линейная функция имеет вид……
+ Система нормальных уравнений для функции у=а0+а1х имеет вид…
+ 
+ Квадратичная функция имеет вид……
+ Система нормальных уравнений для функции у=а0+а1х+а2х 2
+ 
+ Обратная пропорциональная зависимость имеет вид…
+ 
+ Система нормальных уравнений для функции 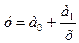имеет вид….
+ 
+ Записать в виде двойного неравенства а0=3,379; ∆а= 0,0004 …
+ Записать в виде двойного неравенства а0=5,647; ∆а= 0,0003 …….
Записать в виде двойного неравенства а0=6,571; ∆а= 0,0002 …….
+ Записать в виде двойного неравенства а0=7,813; ∆а= 0,0005 …….
+ Записать в виде двойного неравенства а0=8,137; ∆а= 0,0007 …….
+ Определить верные цифры числа а=945,673±0,03 ……
+ Определить верные цифры числа а=123,342±0,02 …
+ Определить верные цифры числа а=228,451±0,04 ……
+ Определить верные цифры числа а=363,843±0,05 ……
+ Определить верные цифры числа а=761,639±0,02 …
+ Определить сомнительные цифры а=945,673±0,03 …
+ Определить сомнительные цифры числа а=123,342±0,02 …
+ Определить сомнительные цифры числа а=228,451±0,04 ……
+ Определить сомнительные цифры числа а=363,843±0,05 …
+ Определить сомнительные цифры числа а=761,639±0,02 …
+ Округлить с точностью до 0,01 число 0,428………
+ Округлить с точностью до 0,01 число 8,993……
+ Округлить с точностью до 0,01 число 25,689………
Округлить с точностью до 0,01 число 2,645……
+округлить с точностью до 0,01 число 16,452……
+ Сложить приближенные числа 14,5+113,76+12,783+11,2161=…
+ Сложить приближенные числа 645,25+102,324+10,2=………
+ Сложить приближенные числа 428,263+264,2+748,35=………
+ Сложить приближенные числа 18,6+121,85+13,495+12,3172=……
+сложить приближенные числа 19,5+133,17+14,387+11,3181=………
+ Приближенным числом аназывают число, незначительно отличающиеся от
+ точного А
+ а называется приближенным значением А по недостатку, если
+а A
+ Под ошибкой или погрешностью ∆а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.
+ Если ошибка положительна А>, то
+∆a > 0
+ Абсолютная погрешность приближенного числа
+ Предельную абсолютную погрешность вводят если
a) число А не известно
+ Предельная абсолютная погрешность
+∆а
+ Определить предельную абсолютную погрешность числа а = 3,14, заменяющего число π
+ Относительная погрешность
+σ = ∆/׀А׀
+ Погрешность, связанная с самой постановкой математической задачи
+погрешность задачи
+ Погрешности, связанная с наличием бесконечных процессов в математическом анализе
+остаточная погрешность
+ Погрешности, связанные с наличием в математических формулах, числовых параметров
+начальном
+ Погрешности, связанные с системой счисления
+погрешность округления
+ Округлить число π = 3,1415926535… до пяти значащих цифр
+ 3,1416
+ Абсолютная погрешность при округлении числа π до трёх значащих цифр
Предельная абсолютная погрешность разности
+∆u=∆x1+∆x2
+ Числовой ряд названия сходящимся, если
+существует предел последовательности его частных сумм
+ Найти ln3 c точностью до 10-5
+1,09861
+ Найти sin 20030I
+0,35
+ С помощью этого метода число верных цифр примерно удваивается на каждом этапе по сравнению с первоначальным количеством
+процесс Герона
+ Методом половинного деления уточнить корень уравнения х4+2х3-х-1=0
+ Используя метод хорд найти положительный корень уравнения
+ Вычислить методом Ньютона отрицательный корень уравнения
+ Используя комбинированный метод вычислить с точностью до 0,005 единственный положительный корень уравнения
+1,04478
+ Найти действительные корни уравнения х-sinх=0,25
+1,17
+ Определить число положительных и число отрицательных корней уравнения х4-4х+1=0
+ Определить нижнее число и верхнее число перемен знаков
+ Определить состав корней уравнения х4+8х3-12х2+104х-20=0
+один положительный и один отрицательный
+ Две матрицы одного и того же типа, имеющие одинаковое число строк и столбцов, и соответствующие элементы их равны, называют
+равными
+ Укажите свойства суммы матриц А+(В+С)=…
+ Укажите свойства суммы матриц А-(В-С)=…
+(А-В)-С
+ Укажите название матрицы –А=(-1)А
+ Заменив в матрице типа m×n строки соответственно столбцами получим
+ С какой матрицей совпадает дважды транспонированная матрица
+с исходной
+ Нахождение обратной матрицы для данной называется
+обращение данной матрицы
+ Максимальный порядок минора матрицы, отличного от нуля, называют
+рангом
+ Разность между наименьшим из чисел m и n и рангом матрицы называется
+дефектом
+ Существующие и имеющие важное значение матричные степенные ряды
+правые и левые
+ Матричные ряды дают возможность определять
+трансцендентные функции матрицы
+Матрица разбитая на клетки, называется клеточной и …
+блочной
+ Если элементы квадратной матрицы, стоящие выше (ниже) главной диагонали, равны нулю, то матрицу называют
+ треугольной
+ Метод, представляющий собой конечные алгоритмы для вычисления корней системы
+ Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
+итерационный метод
+ Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
+ Целый однородный полином второй степени от n переменных называется
+квадратичной формой
+ Квадратичная форма называется положительно (отрицательно) определенной, если она принимает положительные (отрицательные) значения, обращаясь в нуль лишь при
+х1=х2=…=хn=0
+ Простейшая форма этого метода заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения
+ Произведением вектора х=(х1,х2,…,хn) на число k называется вектор
+ Для векторов x и y естественно определяется линейная комбинация
+ Любая совокупность n-мерных векторов, рассматриваемая с установленными в ней операциями сложения векторов и умножения вектора на число, не выводящими за пределы этой совокупности называется
+ линейным векторным пространством
Максимальное число линейно независимых векторов n-мерного пространства Еn в точности равно
+ размерности этого пространства
+ Название любой совокупности n линейно независимых векторов n-мерного пространства
Как иначе называют метод бисекций?
+ Метод половинного деления
+ Методы решения уравнений делятся на:
+ Прямые и итеративные
+Кто опубликовал формулу для решения кубического уравнения?
+ Кардано
+ Основная теорема алгебры:
+ Уравнение вида α0xn + α1xn-1 + …+ αn-1x + αn=0 имеет ровно n корней, вещественных или комплексных, если k-кратный корень считать за k корней
+Отделение корней можно выполнить двумя способами:
+аналитическим и графическим
+ Укажите первую теорему Больцано-Коши:
+Если функция f(x) определена и непрерывна на отрезке [α;b] и принимает на его концах значения разных знаков, то на[α;b] содержится, по меньшей мере, один корень уравнения f(x)=0
+Отделим корни уравнения х3 – 2х – 3=0
+Единственный корень расположен между √⅔ и ∞
+При контроле решения алгебраического уравнения может быть полезна:
+Теорема Виета
+Итерация iteratio в переводе с латинского:
+Укажите рекуррентную формулу метода простой итерации:
+От латинского слова recurrens:
+ Последовательность, удовлетворяющая условию Коши, называется:
+фундаментальной последовательностью
+ Метод хорд-
+Частный случай метода итераций
+Усиливает надежность метода
+ Как иначе называют метод Ньютона?
+ Как иначе называют метод хорд?
+Метод пропорциональных частей
+ Метод хорд имеет еще одно имя:
+Метод пропорциональных частей
+ Что общего у метода хорд и метода итераций?
+Общая скорость и свойство самоисправляемости
+обладает свойством самоисправляемости и имеет высокую скорость сходимости
+ Методом хорд уточнить корень уравнения х3 – 2х – 3=0, ξ[1;2]; ε=10-3
+ Предел суммы S ≈ υ(τ1)∆t1+υ(τ2)∆t2+…+υ(τn)∆tn называется:
+ Если сила постоянна, ответ дается формулой:
+A=F(b-а)
+ Все методы вычисления интегралов делятся на:
+Точные и приближенные
+ Точный метод вычисления интегралов был предложен:
+Ньютоном и Лейбницем
+ Геометрически нижняя сумма Дарбу равна:
+Площади ступенчатого многоугольника, содержащегося в криволинейной трапеции
+ Геометрически верхняя сумма Дарбу равна:
+Площади ступенчатого многоугольника, содержащего внутри себя криволинейную трапецию
+ Приближенные методы вычисления интегралов можно разделить на 2 группы:
+аналитические и численные
+ Сущность метода Симпсона заключается в том, что через три последовательные ординаты разбиения проводится…
+ Методы численного интегрирования для вычисления применимы тогда, когда
+невозможно определить первообразную F(x);
+ Наиболее грубым методом численного интегрирования является метод
+прямоугольников;
+ Необходимым условием применения формул Симпсона является: число точек разбиения должно быть
+ Заранее известно, что функция описывается полиномом второй степени (квадратным уравнением). Укажите метод (из числа рассмотренных), который позволит вычислить определенный интеграл без погрешности (погрешность округления не учитывать).
+метод Симпсона;
+ Реккурентное уравнение решения алгебраических уравнений имеет вид: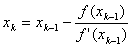 
в методе ……..
+ Идея последовательного исключения неизвестных при решении системы линейных алгебраических уравнений лежит в основе ……
+ При использовании какого метода вычисление интеграла заменяют вычислением некоторой суммы….
+Метод интерполяционных квадратурных формул
+ Простейшая из квадратурных формул, имеющая такой вид: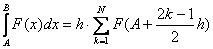 
называется:
+ Какие ошибки экспериментальных данных обычно дают отклонение в одну сторону от истинного значения измеряемой величины?
+ Какой группы методов для решения математических задач не существует?
+ Какой вид локальной интерполяции является простейшим и часто используемым?
+ Приближенные методы вычисления интегралов можно разделить на 2 группы:
+аналитические и численные
+ Если точное число 245,21, а приближенное число 246, то абсолютной погрешностью будет число:
+ Если в матрице число столбцов равно числу строк, то матрица называется:
+ Если в матрице число строк не равно числу столбцов то матрица называется
+ Если у диагональной матрицы все элементы главной диагонали равны, то такая матрица является:
+ При транспонировании матрицы её определитель:
+ Определитель матрицы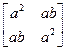 
равен:
+ 
+ Способ решения систем линейных алгебраических уравнений, заключающийся в составлении матрицы из коэффициентов и вектора из свободных членов, с последующим нахождением обратной матрицы, является методом