евклидова геометрия что это
Евклидова геометрия
Полезное
Смотреть что такое «Евклидова геометрия» в других словарях:
ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА ГЕОМЕТРИЯ, система геометрии, основанная на АКСИОМАХ, сформулированных в книге ЕВКЛИДА «Начала». Исходя из набора самоочевидных положений (аксиом) и пользуясь жесткой логикой, Евклид пришел к ряду важных результатов. Его выводы… … Научно-технический энциклопедический словарь
ЕВКЛИДОВА ГЕОМЕТРИЯ — (элементарная геометрия) (см.) пространства, описываемая системой аксиом и постулатов, изложенных древнегреческим математиком и астрономом Евклидом (III в. до н. э.) в его главном труде «Начала». Древние понятия и преобразования, приведенные в… … Большая политехническая энциклопедия
ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА геометрия, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Современная энциклопедия
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систематическое построение которой было осуществлено в Началах Евклида. Возникновение Евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.) Длительный процесс… … Большой Энциклопедический словарь
Евклидова геометрия — ЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Иллюстрированный энциклопедический словарь
Евклидова геометрия — (или элементарная геометрия) геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.). Содержание 1 Основные сведения 2 Аксиоматика … Википедия
евклидова геометрия — геометрия, систематическое построение которой было осуществлено в «Началах» Евклида. Возникновение евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (например, прямые линии натянутые нити и т. п.). Длительный… … Энциклопедический словарь
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систе матич. построение к рой было осуществлено в Началах Евклида. Возникновение Е. г. связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.). Длит. процесс углубления наших… … Естествознание. Энциклопедический словарь
Евклидова геометрия — геометрия, построенная на базе аксиом абсолютной геометрии (являющейся общей частью как евклидовой, так и геометрии Лобачевского) и знаменитой аксиомы Евклида о параллельных (через точку А, не принадлежащую прямой а, в плоскости, определяемой… … Начала современного естествознания
Евклидова (элементарная) геометрия
Евклидова геометрия — это геометрическая теория, основанная на системе аксиом, которая была впервые изложена в третьем веке до нашей эры великим древнегреческим математиком Евклидом в грандиозном научном труде «Начала».
Система аксиом Евклида базируется на основных геометрические понятиях таких, как точка, прямая, плоскость, движение, а также на следующие отношения: «точка лежит на прямой на плоскости», «точка лежит между двумя другими».
В «Началах» Евклид представил следующую аксиоматику:
Тщательное изучение аксиоматики Евклида во второй половине XIX века показало её неполноту. В 1899 году Д. Гилберт предложил первую строгую аксиоматику евклидовой геометрии. Впоследствии еще не раз ученые предпринимали попытки усовершенствовать аксиоматику евклидовой геометрии. Кроме аксиоматики Гилберта, известными считаются: аксиоматики Тарского и аксиоматики Биргофа, которая состоит всего лишь из 4 аксиом.
В современной трактовке система аксиом Евклида может быть разделена на пять групп:
Евклидова геометрия стала результатом систематизации и обобщения наглядных представлений человека об окружающем мире. Углубленное проникновение в суть геометрии привело к более абстрактному пониманию науки. Более поздние достижения и открытие показали, что наши представления о пространстве являются априорными, то есть чисто умозрительные. Таким образом было поставлено под сомнение существование единственной геометрии. бурное развитие физики и астрономии, доказало, что евклидова геометрия описывает структуру окружающего пространства, но вовсе не способна описать свойства пространства, связанные с перемещениями тел со скоростями, близкими к световой. Русский математик Н. И. Лобачевский разработал новую неевклидову геометрию, которая приблизилась к реальному описанию физического пространства.
Евклидова геометрия
Евкли́дова геоме́трия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.).
Содержание
Основные сведения
Элементарная геометрия — геометрия, определяемая в основном группой перемещений (изометрий) и группой подобия. Однако содержание элементарной геометрии не исчерпывается указанными преобразованиями. Так, к элементарной геометрии также относят преобразование инверсии, вопросы сферической геометрии, элементы геометрических построений, теорию измерения геометрических величин и другие вопросы.
Элементарную геометрию часто называют евклидовой геометрией, так как первоначальное и систематическое её изложение, хотя и недостаточно строгое, было в «Началах» Евклида. Первая строгая аксиоматика элементарной геометрии была дана Гильбертом. Элементарная геометрия изучается в средней общеобразовательной школе.
Аксиоматика
Проблема полной аксиоматизации элементарной геометрии — одна из проблем геометрии, возникшая в Древней Греции в связи с критикой этой первой попытки построить полную систему аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.
В «Началах» Евклида была дана следующая аксиоматика:
Исследование системы аксиом Евклида во второй половине XIX века показало её неполноту.
В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром, Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.
Существуют и другие современные аксиоматики, наиболее известные:
См. также
Литература
Полезное
Смотреть что такое «Евклидова геометрия» в других словарях:
ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА ГЕОМЕТРИЯ, система геометрии, основанная на АКСИОМАХ, сформулированных в книге ЕВКЛИДА «Начала». Исходя из набора самоочевидных положений (аксиом) и пользуясь жесткой логикой, Евклид пришел к ряду важных результатов. Его выводы… … Научно-технический энциклопедический словарь
ЕВКЛИДОВА ГЕОМЕТРИЯ — (элементарная геометрия) (см.) пространства, описываемая системой аксиом и постулатов, изложенных древнегреческим математиком и астрономом Евклидом (III в. до н. э.) в его главном труде «Начала». Древние понятия и преобразования, приведенные в… … Большая политехническая энциклопедия
ЕВКЛИДОВА ГЕОМЕТРИЯ — ЕВКЛИДОВА геометрия, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Современная энциклопедия
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систематическое построение которой было осуществлено в Началах Евклида. Возникновение Евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.) Длительный процесс… … Большой Энциклопедический словарь
Евклидова геометрия — ЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, описывающая простейшие свойства физического пространства. Исходными объектами евклидовой геометрии являются точки, прямые, плоскости. Основные положения евклидовой геометрии сосредоточены в системе аксиом, первая… … Иллюстрированный энциклопедический словарь
евклидова геометрия — геометрия, систематическое построение которой было осуществлено в «Началах» Евклида. Возникновение евклидовой геометрии связано с наглядными представлениями об окружающем нас мире (например, прямые линии натянутые нити и т. п.). Длительный… … Энциклопедический словарь
Евклидова геометрия — геометрия, систематическое построение которой было впервые дано в 3 в. до н. э. Евклидом. Система аксиом Е. г. опирается на следующие основные понятия: точка, прямая, плоскость, движение и следующие отношения: «точка лежит на прямой на… … Большая советская энциклопедия
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, систе матич. построение к рой было осуществлено в Началах Евклида. Возникновение Е. г. связано с наглядными представлениями об окружающем нас мире (напр., прямые линии натянутые нити и т. п.). Длит. процесс углубления наших… … Естествознание. Энциклопедический словарь
Евклидова геометрия — геометрия, построенная на базе аксиом абсолютной геометрии (являющейся общей частью как евклидовой, так и геометрии Лобачевского) и знаменитой аксиомы Евклида о параллельных (через точку А, не принадлежащую прямой а, в плоскости, определяемой… … Начала современного естествознания
НЕЕВКЛИДОВА ГЕОМЕТРИЯ
НЕЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности.
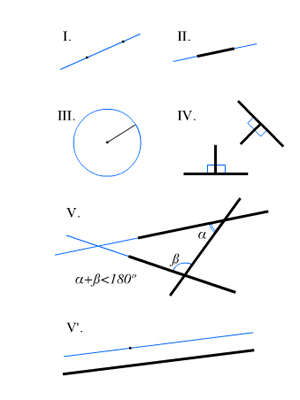
Второй постулат Евклида утверждает, что любой отрезок прямой можно неограниченно продолжить. Евклид, по-видимому, считал, что этот постулат содержит в себе и утверждение, что прямая имеет бесконечную длину. Однако в «эллиптической» геометрии любая прямая конечна и, подобно окружности, замкнута.
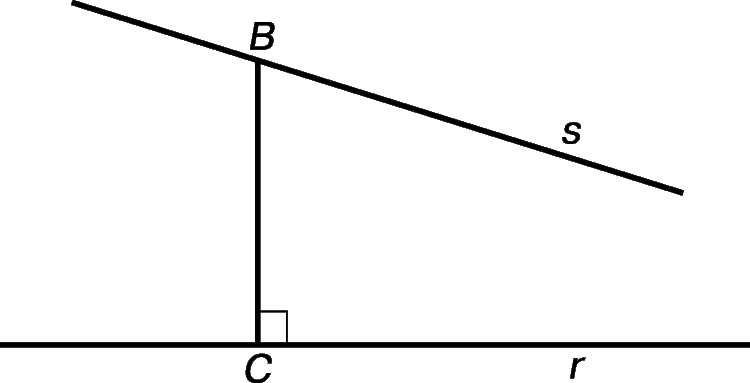
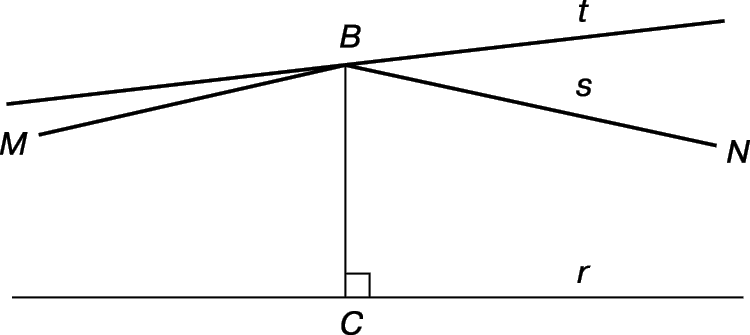
Пятый постулат утверждает, что если прямая пересекает две данные прямые так, что два внутренних угла по одну сторону от нее в сумме меньше двух прямых углов, то эти две прямые, если продолжить их неограниченно, пересекутся с той стороны, где сумма этих углов меньше суммы двух прямых. Но в «гиперболической» геометрии может существовать прямая CB (рис. 1), перпендикулярная в точке С к заданной прямой r и пересекающая другую прямую s под острым углом в точке B, но, тем не менее бесконечные прямые r и s никогда не пересекутся.
Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180 ° в евклидовой геометрии, больше 180 ° в эллиптической геометрии и меньше 180 ° в гиперболической геометрии.
История.
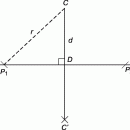
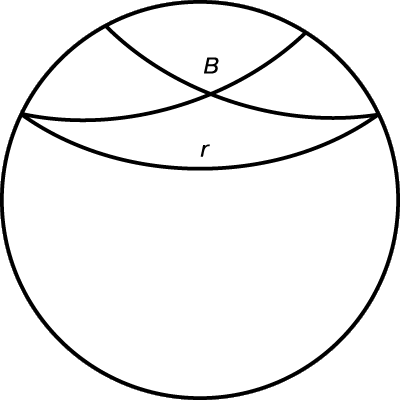
Первым неевклидовым геометром, вероятно, можно считать самого Евклида. Его нежелание использовать «несамоочевидный» пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как «две параллельные линии всюду равно удалены друг от друга» или «любые три точки, не расположенные на одной прямой, принадлежат окружности». Ближе всех подошел к цели иезуит, логик и математик Дж.Саккери (1667–1733), который начал свои исследования с так называемого четырехугольника Саккери (рис. 2), т.е. с четырехугольника BCED, у которого BC = DE, а углы при вершинах C и E прямые. Заметив, что углы при вершинах B и D обязательно равны, Саккери рассмотрел поочередно три гипотезы: верхние углы четырехугольника тупые, прямые и острые. Он доказал, что любая из этих гипотез, если ее принять для какого-нибудь одного такого четырехугольника, остается в силе для всех таких четырехугольников. Саккери намеревался обосновать гипотезу о том, что верхние углы прямые, доказав, что любая другая гипотеза приводит к противоречию. Вскоре он отверг гипотезу о тупом угле (и тем самым лишил себя возможности открыть эллиптическую геометрию), поскольку, как и все геометры до 1854, рассматривал второй постулат как утверждение о том, что прямая имеет бесконечную длину, и отказываться от этого постулата он не хотел. Точно также Саккери в конце концов отверг и гипотезу об остром угле, но прежде, чем принять это ошибочное решение, он, сам того не ведая, открыл многие теоремы геометрии, получившей впоследствии название гиперболической.
К.Гаусса (1777–1855) принято считать одним из величайших математиков всех времен. Он первым подошел к проблеме с современной точки зрения, согласно которой геометрию, отрицающую пятый постулат, надлежит развивать ради нее самой, не ожидая, что при этом возникнет какое-то противоречие. Письма Гаусса к друзьям говорят о том, что к 1816 он преодолел традиционный предрассудок относительно неизбежности противоречия и развил «антиевклидову» геометрию, удовлетворяющую гипотезе Саккери об остром угле. Но, опасаясь насмешек, он воздерживался от публикации этих идей и тем самым позволил разделить честь открытия гиперболической геометрии (примерно в 1825) венгру Я.Бойяи (1802–1860) и русскому Н.И.Лобачевскому (1793–1856). Бойяи опубликовал свою работу до того, как услышал о Лобачевском, а последний, судя по всему, так никогда и не узнал об исследованиях Бойяи.
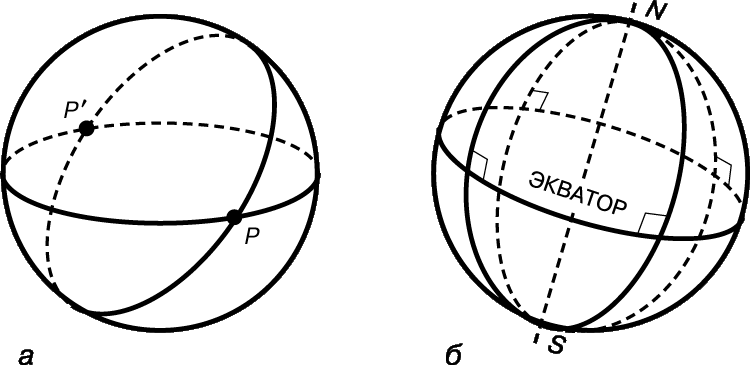
В 1854 Б.Риман (1826–1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.
Эллиптическая плоскость.
Такое представление с помощью диаметров и диаметральных плоскостей сферы (при котором диаметр, соединяющий северный и южный полюсы сферы, является «полюсом» экватора), показывает, что все свойства действительной проективной плоскости сохраняются и для эллиптической плоскости.
Геометрия порядка.
Один из подходов к построению гиперболической геометрии исходит из некоторых фундаментальных аксиом порядка, справедливых и в евклидовой, но не в эллиптической геометрии. Если считать «точки» исходными понятиями, то запись [ABC] означает, что точка B лежит «между» точками A и C (это первичное отношение мы принимаем, не пытаясь его определить). Первые четыре аксиомы порядка утверждают, что 1) существует по крайней мере две точки; 2) если A и B – две различные точки, то существует по крайней мере одна точка C, для которой [ABC]; 3) эта точка C отлична от точки A и 4) порядок [ABC] влечет за собой [CBA], но не [BCA]. «Отрезок» AB, по определению, состоит из точек P, для которых [APB], а «луч» A/B («исходящий из A в другую сторону, чем B») – из точек Q, для которых [QAB]. «Прямая» AB состоит из отрезка AB, точек A, B и двух лучей A/B, B/A. Пятая аксиома утверждает, что если C и D – различные точки на прямой AB, то A лежит на прямой CD (из этой же аксиомы следует, что прямые AB и CD совпадают). Шестая аксиома дает нам точку вне данной прямой, а седьмая, сформулированная М.Пашем (1843–1931), позволяет определить плоскость как множество всех точек, коллинеарных с парами точек на одной или двух сторонах данного треугольника.
Абсолютная геометрия.
Множество прямых, параллельных данному лучу, называется «пучком параллельных»; он содержит единственную прямую, проходящую через любую заданную точку. Следуя аналогии с обычным пучком (состоящим из всех прямых, проходящих через точку), мы можем считать, что пучок параллельных определяет «бесконечно удаленную точку», или, по терминологии Д.Гильберта (1862–1943), «конец». Вместо того, чтобы говорить, что два луча (или две прямые) параллельны или что они принадлежат некоторому пучку параллельных M, мы говорим, что два луча имеют общий конец M. Луч, проходящий через точку C и принадлежащий данному пучку параллельных, принято обозначать CM, как если бы это был отрезок; тот же символ CM можно использовать и для обозначения всей прямой. Если BM и CM – параллельные лучи, то фигура MCB называется «асимптотическим треугольником», поскольку она во многом ведет себя, как обычный треугольник. В частности, два асимптотических треугольника конгруэнтны, если у них имеется по конгруэнтной стороне и конгруэнтному углу.
Гиперболическая плоскость.
Из абсолютной геометрии Бойяи можно вывести евклидову геометрию, добавив евклидову (или аффинную) аксиому: через точку B, не лежащую на данной прямой r, можно провести не более одной прямой, параллельной данной. Гиперболическую геометрию можно вывести из абсолютной геометрии, добавив гиперболическую аксиому, повторяющую только что приведенную, но без отрицания «не» во втором случае. Таким образом, лучи BM и BN на рис. 4 могут быть оба параллельны r, а если M и N их концы, то r называется «прямой MN». Любая прямая, например t, являющаяся продолжением стороны угла Р NBM, образует с r пару «гиперпараллельных», т.е. пару прямых, которые не пересекаются и не параллельны. Две такие прямые имеют единственный общий перпендикуляр. Множество прямых, перпендикулярных данной прямой a, называются «пучком гиперпараллельных» с «осью» a.
Одной из самых прекрасных страниц в литературе по неевклидовой геометрии со времен Лобачевского считается предложенное Г.Либманом доказательство того, что площадь треугольника остается конечной, когда две (или три) его стороны становятся бесконечными. Доказательство сводится к разбиению асимптотического треугольника на бесконечную последовательность конечных треугольников и перекладыванию их с соблюдением одного условия: все они должны умещаться внутри некоторого конечного пятиугольника. Метод Либмана восполняет один из двух недостающих шагов в предложенном Гауссом красивом доказательстве того, что площадь любого треугольника пропорциональна его «угловому дефекту» – величине, показывающей, насколько сумма углов треугольника меньше двух прямых. Аналогия с выражением (A + B + C) – p для площади сферического треугольника (на единичной сфере) наводит на мысль о естественной единице измерения, при которой площадь треугольника ABC просто равна p –(A + B + C). Используя эту единицу, Лобачевский выразил угол параллельности, соответствующий расстоянию x, формулой
Кривые, ортогональные обычному пучку прямых, имеют вид концентрических окружностей; кривые, ортогональные пучку параллельных, имеют вид концентрических «орициклов». В действительности орицикл – это предельная форма окружности, центр которой уходит в бесконечность (так, что диаметры окружности становятся параллельными).
Евклидовы модели неевклидовых геометрий.
Ф.Вахтер (1792–1817) за несколько месяцев до безвременной кончины сообщил в письме к Гауссу о своем наблюдении: если пятый постулат Евклида ложен, то сфера, радиус которой стремиться к бесконечности, приближается к предельной поверхности, чья внутренняя геометрия совпадает с геометрией евклидовой плоскости. Тем самым Вахтер предвосхитил появление «орисферы», сыгравшей важную роль в работах Бойяи и Лобачевского. Эта поверхность получается при вращении орицикла вокруг любого из его диаметров. Кривые на орисфере, которые ведут себя, как евклидовы прямые, – орициклы, по которым орисферу пересекают ее диаметральные плоскости.
СОДЕРЖАНИЕ
элементы
В Элементах 13 книг :
В книгах I – IV и VI обсуждается геометрия плоскости. Доказано множество результатов о плоских фигурах, например: «В любом треугольнике два угла, взятые вместе любым способом, меньше двух прямых». (Книга I, предложение 17) и теорема Пифагора «В прямоугольных треугольниках квадрат на стороне, образующей прямой угол, равен квадратам на сторонах, содержащих прямой угол». (Книга I, предложение 47)
Аксиомы
Ближе к началу первой книги Элементов Евклид дает пять постулатов (аксиом) для плоской геометрии, сформулированных в терминах конструкций (в переводе Томаса Хита):
Хотя Евклид только явно утверждает существование сконструированных объектов, в его рассуждениях они неявно предполагаются уникальными.
Элементы также включают в себя следующие пять «общих понятий»:
Современные ученые согласны с тем, что постулаты Евклида не обеспечивают полного логического основания, которое Евклид требовал для своего выступления. Современные методы лечения используют более обширные и полные наборы аксиом.
Параллельный постулат
Можно сформулировать множество альтернативных аксиом, которые логически эквивалентны постулату параллельности (в контексте других аксиом). Например, аксиома Playfair гласит:
На плоскости через точку, не лежащую на данной прямой, можно провести не более одной линии, которая никогда не пересекает данную линию.
Методы доказательства
Система измерения и арифметики
Измерения площади и объема производятся на основе расстояний. Например, прямоугольник шириной 3 и длиной 4 имеет площадь, представляющую произведение, 12. Поскольку эта геометрическая интерпретация умножения была ограничена тремя измерениями, не существовало прямого способа интерпретации произведения четырех или более чисел, и Евклид избегал таких произведений, хотя они подразумеваются, например, в доказательстве книги IX, предложение 20.
Обозначения и терминология
Именование точек и фигур
Дополнительные и дополнительные углы
Современные версии обозначений Евклида
Современные школьные учебники часто определяют отдельные фигуры, называемые линиями (бесконечными), лучами (полубесконечными) и отрезками линий (конечной длины). Евклид, вместо того чтобы обсуждать луч как объект, который простирается до бесконечности в одном направлении, обычно использовал бы такие выражения, как «если бы линия удлинялась до достаточной длины», хотя иногда он упоминал «бесконечные линии». «Линия» у Евклида могла быть как прямой, так и изогнутой, и при необходимости он использовал более конкретный термин «прямая линия».
Некоторые важные или хорошо известные результаты
Теорема Пифагора утверждает, что сумма площадей двух квадратов на катетах ( a и b ) прямоугольного треугольника равна площади квадрата на гипотенузе ( c ).
Pons Asinorum
Конгруэнтность треугольников
Треугольники конгруэнтны, если у них все три стороны равны (SSS), две стороны и угол между ними равны (SAS) или два угла и одна сторона равны (ASA) (Книга I, предложения 4, 8 и 26). Треугольники с тремя равными углами (AAA) похожи, но не обязательно совпадают. Кроме того, треугольники с двумя равными сторонами и прилегающим углом не обязательно равны или конгруэнтны.
Сумма углов треугольника
теорема Пифагора
Знаменитая теорема Пифагора (книга I, предложение 47) утверждает, что в любом прямоугольном треугольнике площадь квадрата, сторона которого является гипотенузой (сторона, противоположная прямому углу), равна сумме площадей квадратов, стороны которых равны две ноги (две стороны, которые встречаются под прямым углом).
Теорема Фалеса
Масштабирование площади и объема
Приложения
Из-за фундаментального статуса евклидовой геометрии в математике непрактично давать здесь более чем репрезентативную выборку приложений.