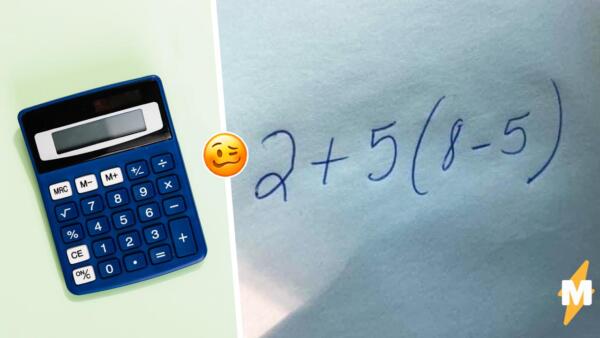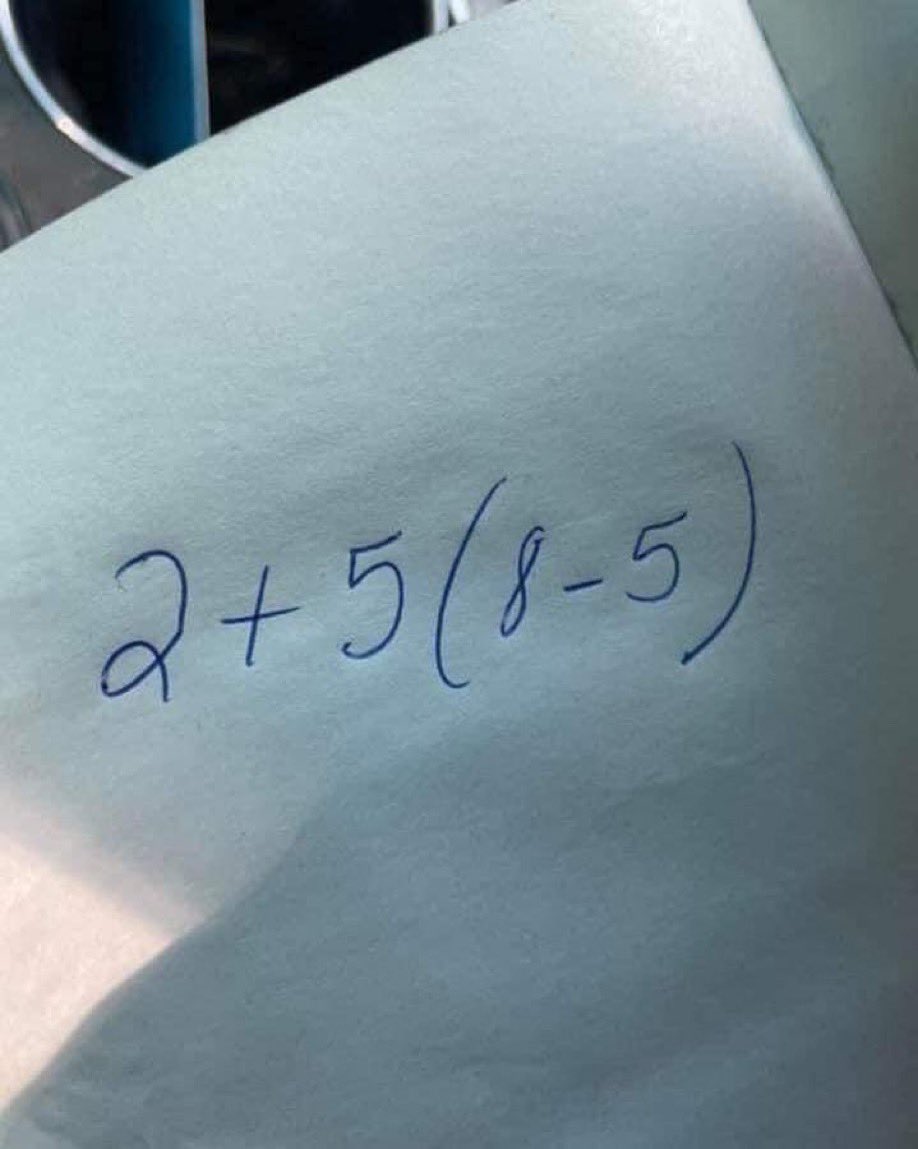как доказать что дважды 2 будет 5
Как доказать что дважды 2 будет 5
Вот вариант без извлечения корней, но с весьма интенсивным жонглированием математическими выражениями.
Сокращаем выражения в скобках: a = b
Вот нарял в инете и заметил такую интересную темку:
Теорема: Дважды два равно пять.
6) Избавимся от квадратов, подставив обе части равенства [4] под знак корня.
Докажите мне, что 2+2=5. Кто докажет, тому накину 100 баллов.
Один философ испытал сильнейшее потрясение, узнав от Бертрана Рассела, что из ложного утверждения следует любое утверждение. Он спросил:Вы всерьез считаете, что из утверждения 2 + 2 = 5″ следует, что вы – папа римский?Рассел ответил утвердительно.И вы можете доказать это?» – продолжал сомневаться философ.Конечно! – последовал уверенный ответ, и Рассел тотчас же предложил такое доказательство.1) Предположим, что 2+2=5.2) Вычтем из обеих частей по два: 2=3.3) Переставим левую и правую части: 3=2.4) Вычтем из обеих частей по единице: 2=1.Папа Римский и я – нас двое. Так как 2=1, то папа римский и я – одно лицо. Следовательно, я – папа римский.»
юмор математика наука философия
Ответы на вопрос: «Докажите мне, что 2+2=5. Кто докажет, тому накину 100 баллов. » Пожалуйста, включите JavaScript для просмотра комментариев.
Математик, программист, невролог и другие
Вчера мы рассказывали вам о любопытных доказательствах существования Бога, представленных разными учёными или талантливыми студентами. Сегодня мы решили рассказать вам ещё о пяти таких теориях.
1. Формула Эйлера, доказывающая существование Бога
Леонард Эйлер (15 апреля 1707-го года — 18 сентября 1783-го года) был швейцарским математиком и физиком, одним из первых сделавшим важнейшие открытия в таких областях, как анализ бесконечно малых и теория графов. Также Эйлер создал большую часть современной математической терминологии и обозначений, в частности, для математического анализа, например, понятие математической функции. Он известен своими работами по механике, гидродинамике, оптике и астрономии. Большую часть своей взрослой жизни он провёл Санкт-Петербурге, Россия, и Берлине, Пруссия.
О религиозных убеждениях.
( кроме одного человека ессно)
И я опять угадываю, кто это!
Чего тут решать! Что такое 2х2? Это два предмета взять два раза. Берём пустой спичечный коробок. В правую руку берём две спички, и две в левую. Кладём в коробок две, потом ещё две. Считаем, сколько в коробке.
А вот как работают «упрямые математики»: они берут картонную коробку, кидают туда по-очереди четыре спички, закрывают коробку крышкой, трясут её, или делают над ней пассы (можно ещё произнести: ахалай-махалай), открывают крышку — а там пять спичек. Ну, так это не математическое доказательство, а фокус.
Старый, всем известный анекдот:
Собеседование при приёме на работу бухгалтера..
— Сколько будет дважды два?
— Четыре, конечно, я математику хорошо знаю.
— Свободны. Следующий.
— Сколько будет дважды два?
Второй же слышал, что первый ответил, и говорит:
— Пять.
— Следующий.
— Сколько будет дважды два?
Этот.
Представим 81/4 как (9/2)^2, 16 как 4^2, 25 как 5^2, 36 как 4х9 и 45 как 5х9. Заодно 36 и 25 умножим и поделим на 2. Равенство станет выглядеть совсем уж страшно:
Однако оно всё ещё верно.
Если приглядеться, можно заметить, что обе части имеют вид a^2-2ab+b^2 (слева a=4, b=9/2, справа a=5, b=9/2). Из школьного курса алгебры известно, что так раскладывается квадрат разности (a-b)^2 Отсюда наше многострадальное равенство можно в очередной раз преобразовать:
Британские ученые доказали, что Бог существует
Дело в том, что Темплтоновская премия — это религиозный аналог Нобеля. Крупную сумму вручают тем ученым, которые своими работами примиряют религию и современную науку. Вот и Мартин Джон Рис попал в число ученых, награжденных этой премией. Вряд ли он часто задумывался о том, как верующие оценят его труды о параллельных мирах и множественных вселенных, формировании галактик и функционировании черных дыр.
Тем не менее, атеизм не помешал ему принять престижную премию, солидный чек и все прочие почести. Подобно большинству прежних лауреатов Темплтоновской премии Рис и в самом деле не имеет никакого отношения к.
На днях в моей ленте сети «ВКонтакте» появилась публикация, которая моментально привлекла внимание. Как говорится, сказался профессиональный азарт. Я думаю, ни один копирайтер не прошёл бы мимо.
Заголовок публикации — «19 фраз, которые продают сами». Конечно, само название уже говорит о том, что в статье очень спорная и противоречивая информация.
Слова и фразы для текста можно провести по аналогии одежды и аксессуаров для человека. Наверное, нам нужно поверить, что есть часы, которые идут всем или рубашка… Или нижнее бельё, со слониками и ромашками…
Я не верю в силу конкретного слова, от которого будет зависеть судьба всего текста. Кроме слов «шара» или «халява», рассчитанных на молочную аудиторию школьников.
Но когда я начал изучать сам список, всё стало (или встало) на свои места…
Слова-терминаторы и «I’ll be back!»
Десятки книг талдычат — будьте аккуратны в своих высказываниях и избегайте слов, которые вы не сможете доказать.
Мы докажем, что 2+2=5, и 95% из вас даже не поймут, в чем подвох
Над этой математической головоломкой бьются лучшие умы мира. А сегодня и вы можете попробовать решить эту задачку. Если вас не пугают неожиданные логические цепочки, обязательно попробуйте решить этот пример!

Знаете ли вы, что 2+2 может быть равно 5? Не торопитесь возмущаться, даже если в школе у вас было «отлично» по математике! Мы не разрушаем основные арифметические постулаты, а лишь предлагаем с неожиданной точки зрения рассмотреть этот простейший пример.
Итак, каким образом при сложении двоек может получиться пятерка? За основу возьмем 0, который также равен 0:
А если из 20 вычесть 20, а из 25 – 25, то мы вновь получим два нуля. Таким образом, получим математически и логически правильное равенство:
20 — 20 = 25 — 25
Следом представим число 20 как 4×5, а 25 – как 5×5. Поэтому далее получаем такое равенство:
(4 x 5) — (4 x 5) = (5 x 5) — (5 x 5)
А на следующем математическом действии с одинаковыми множителями просто выносим 4 в первой половине и 5 во второй части равенства за скобки. Получаем:
4 x (5 — 5) = 5 x (5 — 5)
Поскольку и в правой, и в левой части равенства одинаковые множители (5 — 5), то по правилам математики мы можем их не учитывать, то есть просто сократить. И получим следующее:
И наконец-то долгожданный финал, если 4 представить как (2 + 2):
2 + 2 = 5
2 х 2 = 5 Доказательство
Представим его как 16 — 36 = 25 — 45
Прибавим к обеим частям 81/4
16 — 36 + 81/4 = 25 — 45 + 81/4
В левой части полный квадрат разности чисел 4 и 9/2
В правой части полный квадрат разности чисел 5 и 9/2
(4 — 9/2) в кв = (5 — 9/2) в кв
Извлекаем квадратный корень из обеих частей уравнения.
Телегин Александр
Комментарии
Николай Хижняк
Завораживающий набор чисел. Сколько на него ни смотрю, всегда задаю себе один и тот же вопрос: почему так получается? Стандартный ответ о квадратном корне — это для деток из яселек.
Интересно, кто-нибудь сумеет проделать подобный фокус в области исключительно положительных чисел, не прибегая к помощи деления на ноль?
Куликов Андрей Сергеевич
В приведённом примере, при извлечении корней из обеих частей тождества, были взяты корни с разными знаками: (4-9/2)=-0,5 и (5-9/2)=+0,5, при которых тождество не сохраняется.
Николай Хижняк
Это общепринятый взгляд. Если быть до конца честным, то знак равенства между тождествами — это самая первая ошибка. Мы сами устанавливаем правило, что 16 = 4 х 4, 25 = 5 х 5, что квадраты разности равны между собой. Все дальнейшее — результат игры по нашим правилам.
Вот вариант без извлечения корней, но с весьма интенсивным жонглированием математическими выражениями.
Пусть с = a + b, где а и b — любые числа.
а2 — b2 = (a — b) (a + b)
Поскольку с = a + b, получаем тождество: a2 — b2 = (a — b) c
Раскрываем скобки: a2 — b2 = aс — bc
Добавляем к обеим частям произведение ab: a2 + ab — b2 = ac — bc + ab
Переносим вправо b2: a2 + ab = ac — bc + ab + b2
Переносим влево ac: a2 + ab — ac = ab — bc + b2
Маленькая группировочка: a (a + b — c) = b (a + b — c)
Сокращаем выражения в скобках: a = b
Так как a и b — произвольные числа, получается, что любое число равно любому числу. Лично я сторонник всеобщего равенства:)))
Куликов Андрей Сергеевич
В приведённой задаче три величины a, b и c связаны между собой двумя уравнениями, т.е. задана система из двух уравнений с тремя неизвестными, дальнейшие вычисления являются преобразованием второго уравнения системы из двух уравнений способом подстановки первого уравнения во второе. Полученное выражение a=b является не всеобщим равенством, а уравнением справедливым только для заданной системы из двух уравнений.
а разве извлекать квадратный корень можно?
Николай Хижняк
Корень извлекать можно и нужно, но всё нужно делать с умом))))
Marion
Сразу возник вопрос: почему рассматривается отвлеченное от изначально заданного примера тождество? Здесь доказывается, что число равно числу, а не выражение 2х2=5 (то есть, по сути, здесь выведено доказательство того, что 4=5, а не того, что 2х2=5). Это сводит на нет всю поставноку данной теоремы в моем понимании, ведь она не доказана. Хотя, конечно, я не профессионал в данной области, а просто интересующийся, так что могу не понимать чего-то.)
Николай Хижняк
Вы точно чего-то не понимаете, впрочем, как и я сам. Действительно, здесь используется довольно распространенный среди шулеров и математиков прием — подтасовка. Ответ подгоняется под условие задачи. Базируется всё на неоспоримом равенстве 2 х 2 = 4. Действиельно, существует бесконечное множество вариантов получения числа 4, где 2 х 2 лиш один из них. Так что обратное утверждение 4 = 2 х 2 является не совсем математически правильным — это один из множества вариантов. В данном примере подобный прём используется с единственной целью — произвести впечатление на публику. Хотя математически пример очень интересный — никто толком не может объяснить, почему так получается и в чем заключается принципиальная ошибка.
Marion
Мм-м! Теперь понятно.) Спасибо за ответ, Николай.))
Неандерталец
Извлекаем квадратный корень из обеих частейуравнения.
не правильное извлечение корня, 4-4,5 берется в модуль, а дальше тождество неверно.
во втором случае, где а+b=с… тоже не верное, так как выражение a+b-c равно нулю, а деление на ноль запрещено) из этого следует a*0=b*0, и получается, что 0=0
Валерий Викторович
Ой, дядя Саша, совсем тебе скучно стало богом быть… На пальцах считать пытаешься, ну раз веж это корень.
Ответ не пять… А — Сколько надо?
Владимир Чепурных
Сконструровали каким-то образом очевидное равенство
(a)^2=(-a)^2
и хотим из него получить следствие
Точно также сконструировали другое равенство
a*0=b*0
и также хотим сделать вывод
На кого расчитаны такие шутки-сюрпризы?
Поступать таким образом сознательно — сравнимо с преступлением. Правила установлены для всех, избранные же хотят от них отступить и ввести в заблуждение остальных. Сами же о существовании таких правил знают.
Однако, это очень современно, если коснуться нашей политической элиты. К примеру: Воровать ни-ни! Но ворует! И примеров тому множество, если посмотреть сайт РосПил.
Георгий
если B отрицательное и больше А — равенство не справедливо, математический парадокс не верен т. к. скобки не сократятся, в случае А отрицательного и больше B аналогично. ПО поводу 4=5, ответ примера 0.5=0.5
Георгий
если B отрицательное и больше А — равенство не справедливо, математический парадокс не верен т. к. скобки не сократятся, в случае А отрицательного и больше B аналогично. ПО поводу 4=5, ответ примера 0.5=0.5
sensornet
это просто доказательство на другой пример не на этот так что это не верно
Алексей
Этот пример доказывает не то, что 4=5, а то что формула квадрата разности ( (а – b )2 = а2 – 2 ab + b 2 ) — не верна.
София
Это софизм. Извлечь корень квадратный из (4-9/2) на множестве действительных чисел нельзя. Допущена ошибка. так что 4 не равно 5
Светлана
согласна с Алексеем, что пример доказывает, что формула квадрата разности ( ( а – b ) 2 = а2 – 2 ab + b2 ) — не верна.
Николай Хижняк
И при чем здесь формула квадрата разности. С нею всё нормально. Принимаем a=b и проверяем фомулу.
Как видите, никаких проблем.
Анастасия
Чистый и красивый софизм. Я своих детей уже приучила искать подвох) Обязательно дам им это)
saneksen
Простой пример по математике озадачил Тайку Вайтити. Как решить задачу для младшей школы со скобками
Простая задача по математике на порядок действий разделила пользователей англоязычного твиттера. Любопытные комментаторы пытаются найти правильный ответ примера для младших классов, используя разные, порой несуществующие математические правила. В споре поучаствовал и актёр Тайка Вайтити, но не попал в «список отличников».
Пример со скобками 28 ноября опубликовал пользователь твиттера с ником MIR (@1RealMir) — комментатор запостил фотографию задания и предложил своим подписчикам поделиться полученными ответами. Задача включала в себя вычитание в скобках и сложение за скобками — автор использовал простые числа, поэтому основной трудностью примера был порядок действий.
Какой ответ вы получили?
Твит развирусился, став для части комментаторов настоящей головоломкой. Одним из самых популярных ответов оказалось число 21 — те, кто в ходе решения получил такую цифру, поделились порядком действий. Так, блогерка Tara Dublin (Taylor’s Version) (@taradublinrocks) расписала этапы решения задачки по очереди — сначала девушка сложила цифры за скобками, затем выполнила вычитание в скобках и в конце умножила числа друг на друга.
Вторым популярным ответом стало число 17 — его получила другая половина комментаторов, тоже поделившаяся ходом решения. Как оказалось, ответившие 17 использовали иной порядок действий — после вычитания в скобках фанаты арифметики выполнили умножение и только потом — сложение.
На пост обратил внимание даже новозеландский актёр и кинорежиссёр Тайка Вайтити. В шуточном твите он предположил, что правильный ответ — 3.
Что за чертовщина — всё это не имеет смысла. Там стоит число 7, а рядом в скобках 3. Можно прочитать, как «7, но на самом деле это 3», так что верное решение — 3.
На самом деле решение задачи кроется в школьном правиле из начальных классов, порядке действий, которое гласит — вначале выполняются действия в скобках, затем приоритет достаётся умножению и делению, а в конце решаются сложение и вычитание. Применяя математические правила, пример решается простым образом — первым выполняется вычитание в скобках, затем умножение, и после последнего действия, сложения, получаем правильный ответ — 17.
Впрочем, споры вокруг задания продолжаются — пользователи Сети, получившие разные ответы, настаивают на своей правоте.
Ранее Medialeaks рассказал, как простая задача на логику вывела из строя трёх инженеров. Молодые специалисты три минуты пытались понять, как из двух цифр 100 получить двести, используя одну чёрточку.
О том, зачем пользователи Сети ищут слово «цвет» в «Яндексе», читайте в материале Medialeaks. Участники флешмоба таким образом гадают, как на палитре выглядит их настроение.
Просто, как дважды два четыре
Наверное, каждый из хабровчан хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс.
И действительно, как же доказать, что 2 × 2 = 4? Ответ под хабракатом.
Дисклеймер
Начнём с начала
Что такое натуральные числа? Четверо из пяти людей, встреченных на улице, ответят:«Это один, два, три и так далее». Более строгая формулировка этого ответа, которую я встретил в школьном учебнике, гласит: натуральные числа — это члены арифметической прогрессии, начинающейся с 1 и имеющей разность 1. Другое определение из учебника: это числа, которые используются для обозначения количества объектов.
До конца XIX века натуральные числа определялись примерно так, либо не определялись вообще, полагаясь чем-то самим собой разумеющимся. А потом началась перестройка: здание математики стали переносить на фундамент теории множеств, и вещи, которые ранее казались элементарными, внезапно потребовали строгого обоснования.
Аксиоматика Пеано
Товарищ Джузеппе Пеано, большой озорник и затейник (чего стоит хотя бы латино-сине-флексионе), создал очень простую и компактную аксиоматику натуральных чисел, используемую и поныне. Натуральные числа в его интерпретации похожи на структуру данных «односвязный список» — правда, бесконечный.
Итак, натуральные числа — это множество ℕ с заданной на нём функцией следования a → a’, которые удовлетворяют следующим трём аксиомам:
1. Для каждого натурального числа a существует единственное следующее за ним число a’.
Эта аксиома означает, что наш односвязный список бесконечен. Нет такого элемента, у которого в поле «next» записан null. Также это именно список, а не какое-нибудь бинарное дерево: у каждого элемента только один следующий.
2. Существует одно и только одно число, не следующее ни за каким другим. Это число называется единицей. Каждое из оставшихся чисел следует ровно за одним числом (спасибо Kozy, в первоначальной редакции я пропустил эту фразу).
У списка должна быть голова, причём только одна. Список не должен зацикливаться (за третьим элементом не может следовать второй).
3. У множества натуральных чисел нет собственного подмножества, удовлетворяющего аксиомам 1-2.
Без этой аксиомы можно было бы, допустим, добавить к множеству натуральных чисел ещё одно число-уроборос, следующее за самим собой. Или ещё два числа, которые следуют друг за другом. Иначе говоря, аксиома 3 не допускает утечек памяти, которые могли бы возникнуть из-за изолированных кусков списка, до которых нельзя добраться по ссылкам, если идти от головы. Если из натуральных чисел можно что-то выкинуть — это не натуральные числа.
Сложение и умножение
Удивительно, но здесь нет ни слова о коммутативности, ассоциативности, дистрибутивности и прочих свойствах сложения и умножения, о которых рассказывают в школе. Все они выводятся из этих четырёх базовых.
2 × 2 = 4
Вооружившись знаниями, мы можем теперь перейти к доказательству. Однако сначала нужно понять две вещи: что такое 2 и что такое 4. Двойка следует за единицей, поэтому 2 = 1′. Четвёрка следует за тройкой, которая, в свою очередь, следует за двойкой, которая, как я уже говорил, следует за единицей — поэтому 4 = 1»’.
Итак, нам нужно доказать следующее: 1′ × 1′ = 1»’.
Сначала докажем, что дважды два — это два плюс два. Действительно,
Теперь докажем, что 2 + 2 = 4.
1′ + 1′ = (1′ + 1)’ (первое свойство сложения)
1′ + 1 = (1′)’ = 1» (второе свойство сложения)
Следовательно, 1′ + 1′ = (1»)’ = 1»’
Заключение
Всякая простая вещь, если вглядываться в неё пристально, через какое-то время перестаёт казаться простой. Натуральные числа и операции над ними — не исключение, а скорее яркий пример. Ещё более сложным и интересным образом в современной математике строятся множества целых, рациональных и действительных чисел. Но это тема совсем другого разговора.
Пост скриптум
Как известно, одна и та же теория может опираться на совершенно разные системы аксиом. У той же аксиоматики Пеано существует куча вариантов, отличающихся по формулировке, но принципиально схожих. Так как же вводится аксиоматика натуральных чисел в школе?
Это не произносится вслух (да школьники к тому моменту и не знают ещё страшных слов типа «множество» и «функция»), но по сути множество натуральных чисел в школе определяется как множество строк специальных символов, называемых цифрами. Строки должны быть конечными, непустыми и не должны начинаться с символа, называемого нулём.
Отношения равенства и неравенства, сложение, вычитание, умножение и деление — всё это определяется через операции над строками символов. Для строк из одного символа (т.е. для отдельных цифр) существуют специальные таблицы — таблицы сложения и умножения. Для более длинных строк специальные правила позволяют свести действия над ними к действиям над отдельными цифрами. Эти правила и таблицы и являются школьной аксиоматикой натуральных чисел.
В таком понимании натуральных чисел «2 × 2 = 4» — часть аксиоматики, поскольку это тождество содержится в таблице умножения. Тогда, действительно, ничего проще быть не может. Но аксиоматику Пеано всё равно знать не вредно.