как доказать что инертная масса равна гравитационной
Равенство гравитационной и инертной массы
Согласно фундаментальным научным положениям Теории Относительности Реальности, разработанной и развиваемой одним из множества рядовых российских мультидисциплинарных исследователей и изобретателей, инерция есть сила реактивного отталкивания коллектива квантовых объектов плотной материи вещества (нейтронов, протонов, ядер атомов и электронов) от испускаемых ими изотропно во все стороны потоков элементарных отдельностей (элементарных вихрей) неплотной материи электростатики и дипольно равное реактивное отталкивание от испускаемых дипольно элементарных отдельностей неплотной материи магнетизма.
Естественно, что при любой скорости равномерного движения по инерции объектов вещества будет сохраняться их изотропное реактивное отталкивание внутрь себя от испускаемых во все стороны и из магнитных полюсов в окружающее пространство неплотной материи вездесущего вакуума.
Гравитация это сила давления на каждый квантовый и на каждый состоящий из множества квантовых объектов плотной материи вещества приблизительно изотропного хаоса движения потоков элементарных отдельностей неплотной материи электростатики и магнетизма, испущенных всем множеством других ближних, дальних и сверх дальних объектов вещества. По проекции взаимной тени в объёме пространства из хаоса этих потоков отдельностей неплотной материи вакуума относительно близко расположенные объекты вещества придавливаются (не притягиваются) друг к другу потоками элементарных отдельностей неплотной материи электростатики и магнетизма, составляющих объём пространства неплотной материи вакуума.
Так что инерция, масса и гравитация это сила инерции реактивного отталкивания от всех сторон внутрь себя и сила давления со всех сторон неплотной материи вакуума равны. В условиях равномерного или неравномерного движения объектов плотной материи вещества по инерции без сопротивления или с сопротивлением неплотной материи вакуума.
Сила тяжести, масса и вес тела, невесомость
Масса
Масса обозначается символом \(m \), является скалярной величиной и в СИ измеряется в килограммах.
Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:
\[ \large \boxed < \begin
От массы зависят инерционные и гравитационные свойства физических тел.
Масса в природе проявляет себя двумя способами. Поэтому, выделяют:
Инертная масса
Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.
Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».
Гравитационная масса
Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.
Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.
Так же, масса входит в формулы для расчета импульса и механической энергии.
Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.
Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.
Сила тяжести
Сила тяжести — это сила, с которой Земля притягивает к себе тело.
\(\large \vec
\(\large m \left(\text<кг>\right) \) — масса тела;
Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.
Является векторной величиной и обозначается символом \(\vec
\).
\(\vec
\left(H\right) \) – вес тела, как любая сила в СИ измеряется в Ньютонах.
Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.
Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу \(\large \vec
Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.
Чем вес отличается от силы тяжести
Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.
Что такое невесомость
Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.
Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.
Как изменяется вес тела лифте
Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.
Если скорость лифта не изменяется
Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.
Примечание: «неизменной», также, значит «постоянной», или «одной и той же».
По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.
Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.
Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:
\[ \large N – m \cdot g = 0 \]
А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).
Прибавив к обеим частям уравнения величину \( m \cdot \vec
По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.
Воспользуемся тем, что \( \left|\vec \right|\), получим То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен \( mg \). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета. Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2). Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах. Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так: \[ \large N – m \cdot g = m \cdot a \] А для рисунка 2б, так: \[ \large N – m \cdot g = — m \cdot a \] Прибавим теперь к обеим частям уравнений величину \( m \cdot g \), получим: \( \large N = m \cdot a + m \cdot g \) – для случая рис. 2а; \( \large N = — m \cdot a + m \cdot g \) – для рис. 2б; Вынесем массу за скобки \( \large N = m \cdot \left( a + g \right) \) – для рис. 2а; Учтем, что \( \left|\vec \right|\), окончательно запишем Для рисунка 2а — движение лифта вверх с ускорением: Вес тела в движущемся с ускорением вверх лифте, будет равен \( m \cdot \left( g + a \right) \), то есть, превышает величину \( m \cdot g \). Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается: Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен \( m \cdot g \). Вес тела в движущемся вниз с ускорением лифте, равен \( m \cdot \left( g — a \right) \), это меньше величины \( m \cdot g \). Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать! Когда вес тела больше силы тяжести, говорят, что возникает перегрузка. \[ \large \boxed < P >m \cdot g >\] Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения \(\large \vec Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз. Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…». Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить. \(P = m \cdot g \) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте. \( P = m \cdot \left( g + a \right) \) — вес, когда лифт движется с ускорением вверх; \( P = m \cdot \left( g — a \right) \) — вес в движущемся вниз с ускорением; Если ускорение лифта при его движении вниз \( a = g \), наступит невесомость, вес тела исчезнет \( P = 0 \). Рис. 1. Прибор для измерения инертной массы космонавтов в невесомости. На космической станции используются массметры, действие которых основано на измерении периода свободных колебаний груза на пружинах [1]. Масса как физическое понятие обладает следующими фундаментальными свойствами: имеет линейные размеры, обладает гравитационными и инерционными свойствами, а также в определенных пропорциях обладает потенциальной и кинетической энергией. В 20-м веке с появлением релятивистских теорий возникли различные понятия массы: электромагнитная масса, динамическая масса, релятивистская масса, масса покоя, активная и пассивная массы (полный анализ масс в монографии М. Джеммера [2]). В данной статье я не буду рассматривать то многообразие релятивистских оттенков массы, т.к. само понятие релятивизм уходит в прошлое. Остановлюсь на классических понятиях масс: инертной и гравитационной. Здесь также нет смысла доказывать, что данные массы эквивалентны, т.к. проверены многочисленными опытами; начинал их еще Галилей, затем Ньютон, Этвеш, Дикке, Брагинский по нарастающей точности измерения подтверждали равенство инертной (тяжелой) и гравитационной масс. Гравитационная масса, это та масса, что фигурирует в законе всемирного тяготения, а инертная масса – та, что ускоряется под действием силы по второму закону Ньютона. Согласно принципу эквивалентности эти массы всегда пропорциональны, а в определенных физических единицах просто равны друг другу. Сам же принцип эквивалентности является неким постулатом, который не доказывается теоретически и не обосновывает его. Фактически этот принцип является гипотезой, т.к. неизвестно, почему инертная масса тела всегда равна гравитационной массе. Данной статьей и последующими статьями, не вдаваясь глубоко в математические завихрения, я попытаюсь на физическом уроне объяснить принцип эквивалентности данных масс. Для начала серьезного разговора о данной формуле следует начать с массы. Эйнштейн, на основании преобразований Лоренца, утверждал, что релятивистская масса с увеличением скорости постоянно растет. «Масса и энергия, таким образом, сходны по существу – это только различные выражения одного и того же. Масса тела не постоянна; она меняется с его энергией» [3]. Судя по выражению (1) когда скорость тела сравняется со скоростью света, то масса данного тела будет фактически бесконечной. Любому обывателю, не говоря о физиках, становится понятно, что такое невозможно. Физики еще добавят, что любому телу, имеющему массу, достичь скорости света невозможно, т.к. для этого потребуется бесконечная энергия. Окунь в своей статье: «Понятие массы» [4] предостерегает об ошибочном толковании возрастания массы от скорости и утверждает, что масса не растет с увеличением скорости. Но что тогда растет – энергия? Согласимся с Окунем, с возрастанием скорости – растет энергия, но она тоже, при приближении к скорости света будет стремиться к бесконечности. И где выход? Вот с такими парадоксами из серии масса-энергия разберемся в последней статье из рубрики «Масса»: «Самое великое заблуждение в физике». В свое время Эйнштейн постулировал, что две разновидности массы, которые кажутся разными, поскольку измеряются в разных экспериментах, в действительности одно и то же. В своей статье Л.Б. Окунь также отмечает: «речь идет не о равенстве двух различных масс, а об одной и той же физической величине – массе, определяющей различные явления». [4] Эквивалентность масс В 19 веке между физиками был затеян спор на счет эквивалентности масс инертной и гравитационной, предполагая, что данные массы действительно разные. В экспериментах измерения массы проводились разными способами, а на самом деле, по существу, масса одна. Поэтому говорить о разных массах одного и того же тела не совсем корректно. Измерения двумя разными способами одной массы приводят к эквивалентности масс. Возьмем формулу Ньютона: Чем большую силу необходимо приложить, чтобы сдвинуть данное тело, тем больше оно будет иметь инертной массы, тем более оно массивно, тем больше оно имеет вес. Понятие массы было введено в физику Ньютоном, до этого естествоиспытатели оперировали понятием веса. Гравитационная сила, действующая на падающее в свободном пространстве тело массой m, определяется по формуле. g – ускорение свободного падения. В данном случае, поскольку тело свободно притягивается, то чем больше g в формуле Всемирного тяготения, то тем больше гравитационная масса. Физики зря затеяли спор по поводу различных масс. Масса, в условиях Земли, всегда и везде одна – она принадлежит одному телу. Не важно, толкать его в бок или бросать с Пизанской башни. «Масса структурного элемента (масса атома или молекулы) по своей сути является гравитационной массой» [5]. Инертная масса – это та же гравитационная масса, т.к. инертная масса отождествляется с весом тела. А что такое вес? Вес – это масса, создаваемая притяжением земли, иначе гравитацией. А это та же самая гравитационная масса. Здесь не следует плодить термины и запутывать самих себя. На Земле есть только одна масса, и у нее не должно быть прилагательных. Тем более, в метрологии измеряют лишь одну гравитационную массу. Вот здесь я хочу сделать два важных уточнения: 1) инертная и гравитационная массы равны только тогда, когда тело, участвующее в двух экспериментах находится при одной и той же температуре; 2) эксперимент должен проводиться в одной лаборатории, в одной инерциальной системе отсчета (ИСО). В первом случае, если температура тела, падающего на землю гораздо ниже, чем в эксперименте с измерением инерции, то инертная масса будет меньше, по причине возникновения плавучести. [6]. Во втором случае, если измерения проводить в разных ИСО, то значения гравитационной и инертной масс также будут разными. К примеру, на космической станции, в условиях невесомости, гравитационная масса равна нулю, но чтобы сдвинуть какое либо тело, а затем остановить его, необходимо приложить, хотя и малую, но силу. В обоих случаях следует добавить еще одно ограничение, в случае если тело движется, то его скорость должна быть много меньше скорости света v˂˂c. А если удалиться за пределы земного тяготения в космическое пространство, например, астероид, движущийся в направлении планеты Земля, находящийся на расстоянии в один световой год. Чтобы избежать столкновения необходимо изменить его направление, т.е. т направить его инертную массу по другому вектору. Для этой операции потребуется приложить огромную силу, в то же время гравитационная масса данного астероида относительно Земли практически равна нулю. Окончательный ответ по поводу эквивалентности двух масс гравитационной и инертной будет дан в последующих статьях. Продолжение следует. Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта: Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду. Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют. Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел. Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс. Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе [1] На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10 −3 ).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10 −13 ). Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью. В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная. В СТО масса тела m определяется из уравнения релятивистской динамики [3] : где E — полная энергия свободного тела, p — его импульс, c — скорость света. Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились. Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния. Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы. Одна из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, состоит в том, что земной шар несколько сплюснут у полюсов и расстояние от центра Земли до её поверхности у полюсов меньше, чем на экваторе. Другой причиной является вращение Земли. Необыкновенное свойство гравитационных сил, как мы уже говорили, объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Масса тела, которая входит во второй закон Ньютона, определяет инертные свойства тела, т. е. его способность приобретать определённое ускорение под действием данной силы. Это инертная масса mи. Казалось бы, какое отношение она может иметь к способности тел притягивать друг друга? Масса, определяющая способность тел притягиваться друг к другу, — гравитационная масса mr. Из механики Ньютона совсем не следует, что инертная и гравитационная массы одинаковы, т. е. что Равенство (3.5) является непосредственным следствием из опыта. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств. Ключевые слова для поиска информации по теме параграфа. Вопросы к параграфу 1.Справедлив ли закон всемирного тяготения для тел произвольной формы? 2. Какие силы называют центральными? 3. Каков физический смысл гравитационной постоянной? 4. От чего зависит ускорение свободного падения? 5. Как доказать, что инертная масса равна гравитационной? Образцы заданий ЕГЭ А 1. К каким двум телам массами m1 и m2 на расстоянии r друг от друга применим закон всемирного тяготения в форме 1) к любым телам при любых расстояниях между ними А 2. Расстояние между центрами двух шаров равно 1 м, масса каждого шара 1 кг. Сила всемирного тяготения между ними равна А 3. При увеличении в 3 раза расстояния между центрами шарообразных тел сила гравитационного притяжения 1) увеличивается в 3 раза 3) увеличивается в 9 раз А 4. По какой из приведённых формул можно рассчитать силу гравитационного притяжения между двумя кораблями одинаковой массы m (см. рис.)? Считайте, что b много больше размеров кораблей. А 5. Два маленьких шарика массой m каждый находится на расстоянии r друг от друга и притягиваются с силой F. Чему равна сила гравитационного притяжения двух других шариков, если масса каждого из них m/2, а расстояние между их центрами 2r?Если скорость лифта изменяется
Что такое перегрузка
Подведем итоги
Как доказать что инертная масса равна гравитационной
Инертная масса
Содержание
Исследование единства понятия массы
Определение массы
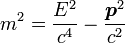
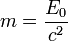
Масса составных и нестабильных систем
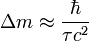
Единицы массы
§ 28. Сила тяжести и сила всемирного тяготения (окончание)
Зависимость ускорения свободного падения тел от географической широты
Равенство инертной и гравитационной масс

Силы тяжести, тяготения. Гравитационная и инертная массы
2) только к небесным телам при больших расстояниях между ними
3) к любым телам с размерами, значительно меньшими расстояния r
4) только к телам шарообразной формы
2) уменьшается в 3 раза 4) уменьшается в 9 раз