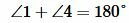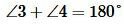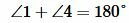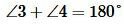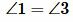как доказать что отрезки параллельны

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

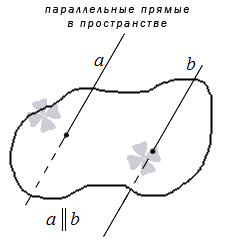
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

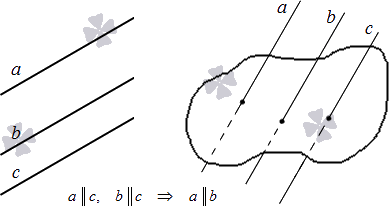
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

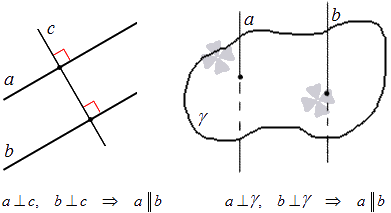
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Параллельность прямых

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Как доказать что отрезки параллельны

Наглядная геометрия 7 класс. Опорный конспект № 3 Параллельные прямые.

В геометрии нельзя «на глазок» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано. Вы уже знаете, что на плоскости справедлива теорема: «Две прямые, перпендикулярные третьей, параллельны между собой».

Есть еще три признака параллельности прямых, которые можно объединить в одну теорему, она так и называется: «Признаки параллельности прямых». Данные признаки связаны с углами, которые образуются при пересечении двух прямых третьей прямой. Это так называемые накрест лежащие углы, соответственные углы и односторонние углы.

Оказывается, что если накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые будут параллельны.

Справедливы и обратные утверждения. Если даны две заведомо параллельные прямые, которые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°.

Ранее мы доказали, что через точку вне прямой можно провести единственную прямую, перпендикулярную данной. Можно также доказать, что через точку, не лежащую на прямой, можно провести прямую, параллельную данной. А вот доказать, что такая прямая — единственная, нельзя! Утверждение «Через точку, не лежащую на прямой, можно провести ЕДИНСТВЕННУЮ прямую, параллельную данной» называется аксиомой параллельных прямых. У Евклида эта аксиома называлась пятым постулатом.

На протяжении двух тысячелетий это утверждение вызывало захватывающие и драматичные споры между такими знаменитыми учеными, как Лобачевский, Гаусс и другие. Споры состояли в том, можно или нельзя доказать этот пятый постулат Евклида на основании уже известных теорем. В конце концов работы в этом направлении привели к полному пересмотру научных представлений о геометрии Вселенной.

При пересечении двух прямых третьей, которая называется секущей, образуется 4 пары накрест лежащих углов, 4 пары соответственных и 4 пары односторонних.

3 и 5; 4 и 6 — внутренние накрест лежащие углы;
1 и 7; 2 и 8 — внешние накрест лежащие углы;
1 и 5; 2 и 6; 4 и 8; 3 и 7 — соответственные углы;
3 и 6; 4 и 5 — внутренние односторонние углы;
2 и 7; 1 и 8 — внешние односторонние углы.

Признаки параллельности прямых. Если накрест лежащие углы равны, ши соответственные углы равны, ши сумма односторонних углов равна 180°, то прямые параллельны. В первую очередь нужно доказать, что если накрест лежащие углы равны, то прямые параллельны. Доказательство опирается на уже доказанное нами свойство: две прямые, перпендикулярные третьей, параллельны между собой. Из середины отрезка секущей опускают перпендикуляр на одну из параллельных прямых. Затем перпендикуляр продляют до пересечения со второй прямой. Из равенства полученных треугольников следует, что прямая, проходящая через перпендикуляр, будет перпендикулярна и второй прямой. Дальнейшее просто.

Через точку, не лежащую на данной прямой, МОЖНО провести прямую, параллельную данной. Опустив перпендикуляр из точки на прямую, а затем, восставив перпендикуляр к проведенной прямой, получим две прямые, перпендикулярные третьей, которые будут параллельны. А вот доказать, что такая прямая единственная, нельзя. Поэтому справедлива АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: «Через точку, не лежащую на данной прямой, проходит ЕДИНСТВЕННАЯ прямая, параллельная данной».

Теорема о двух прямых, параллельных третьей. Две прямые, параллельные третьей, параллельны между собой. Если бы они пересекались, то через одну точку проходили бы две прямые, параллельные третьей.

Теорема о пересечении параллельных прямых. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Если бы эта прямая не пересекала вторую прямую, то она была бы ей параллельна. Но тогда через одну точку проходили бы две прямые, параллельные третьей. А это невозможно.

Свойства углов при параллельных прямых и секущей. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°. В первую очередь нужно доказать, что если прямые параллельны, то накрест лежащие углы равны. Пусть прямые параллельны, а накрест лежащие углы 1 и 2 не равны. Отложим угол, равный углу 2, как показано на рисунке. Получим еще одну прямую, параллельную нижней прямой (если накрест лежащие углы равны, то прямые параллельны). Но через точку нельзя провести две прямые, параллельные третьей. Значит, наше предположение неверно, и накрест лежащие углы равны. Остальное несложно.

Из указанных свойств параллельных прямых вытекает важное следствие: перпендикуляр к одной из параллельных прямых будет перпендикуляром и к другой. Доказательство следует из равенства соответственных углов.

Теорема об углах с соответственно параллельными сторонами. Углы с соответственно параллельными сторонами равны, если они одновременно острые ши одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Продлив стороны данных углов, получим две пары равных соответственных углов, откуда ∠1 = ∠2. Продлив сторону угла 1 за его вершину, получим доказательство второй части теоремы.

Теорема об углах с соответственно перпендикулярными сторонами. Углы с соответственно перпендикулярными сторонами равны, если они одновременно острые или одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Проведя перпендикулярные лучи из вершины угла 1, получим, что углы 2 и 3 равны и углы 3 и 1 дополняют один и тот же угол 4 до 90°. Значит, ∠1 = ∠3, ∠1 = ∠2. Продлив сторону угла 2 за его вершину, получим доказательство второй части теоремы.

Это опорный конспект № 3 по геометрии в 7 классе «Параллельные прямые (опорный конспект)». Выберите дальнейшие действия:

Источник

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Если прямые a и b параллельны, то это обозначают так:

На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

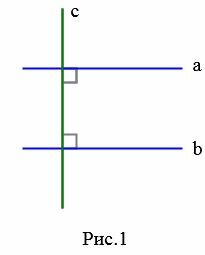Понятие параллельности можно распространять и на отрезки.

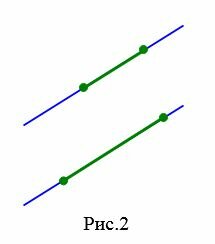Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

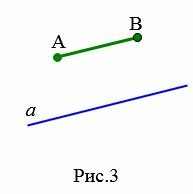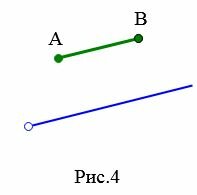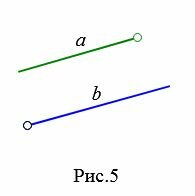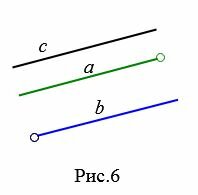На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

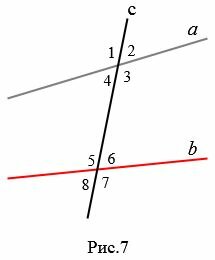Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

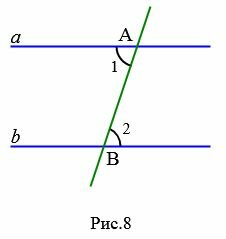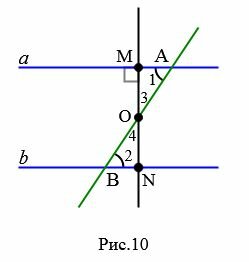
Докажем, что .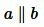

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

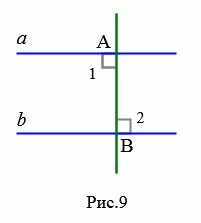Предположим, что углы 1 и 2 не прямые (Рис.10).

Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

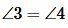
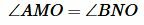
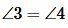
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

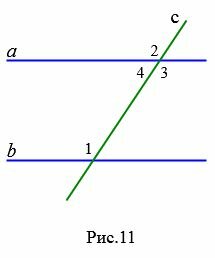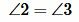
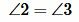
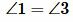
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Источник