как доказать что прямые пересекаются в одной точке

Пересечение прямых. Точка пересечения двух прямых

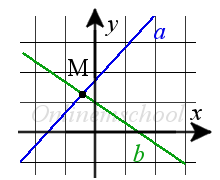
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Точка пересечения двух прямых на плоскости

Если система уравнений:

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Вычтем из первого уравнения второе

Из первого уравнения найдем значение x

Подставим значение x во второе уравнение и найдем значение y

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

В первое уравнение подставим значения x и y из второго и третьего уравнений.

Подставим значение t во второе и третье уравнение

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Из второго уравнения выразим y через x

Подставим y в первое уравнение

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k ₁ = k ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

Вычтем из первого уравнения второе

Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.

Точка пересечения двух прямых в пространстве

Если система уравнений:

Решение: Составим систему уравнений

К шестому уравнению добавим пятое уравнение

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

Подставим значение t из шестого уравнения в остальные уравнения

Источник

Докажите, что прямые пересекаются в одной точке

Докажите, что отрезки пересекаются в одной точке
Четырехугольник ABCD-параллелограмм; O1 и О2- центры окружностей, вписанных в D ABC и в D ADC.

Доказать, что прямые на которых лежат высоты тупоугольного треугольника пересекаются в одной точке
как доказать, что прямые на которых лежат высоты тупоугольного треугольника пересекаются в одной.

Докажите, что все четыре медианы пересекаются в одной точке и точкой пересечения делятся в соотношении 3:1
Медианой четырёхугольника назовем отрезок, соединяющий какую-нибудь из его вершин с центром медиан.

Докажите, что прямые лежат в одной плоскости
докажите, что все различные прямые, пересекающие одну из скрещивающихся(мимобежащих) прямых и.

Доказать, что плоскости пересекаются в одной точке
Доказать, что плоскости 2х-3у-z+15=0 3x+y-4z=0 и 5x-2y+3z-1=0 пересекаются в одной точке и найти.

Доказать, что медианы тетраэдра пересекаются в одной точке
Доказать, что меридианы тетраэдра пересекаются в одной точке и делятся в отношении 3:1, считая от.

Доказать, что медианы треугольника пересекаются в одной точке и делятся в отношении 2 : 1.
Доказать, что медианы треугольника пересекаются в одной точке и делятся в отношении 2 : 1.

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник причем – точка ее пересечения со стороной – точка ее пересечения со стороной и – точка ее пересечения с продолжением стороны

Тогда выполняется равенство:

Как это запомнить? Сначала рисуем треугольник Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и причем на стороне должна лежать точка на стороне – точка и на продолжении – точка

Затем записываем равенство так, как будто «обходим» весь треугольник от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и – их тоже включаем в формулу.

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек и выполняется равенство: – то это означает, что точка лежит на отрезке Или, если нам удается доказать, что угол – развернутый, это и будет означать, что точки и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и – лежат на одной прямой.

Теорема Чевы

Пусть точки и лежат соответственно на сторонах и треугольника причем отрезки и пересекаются в одной точке. В этом случае выполняется равенство:

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Это значит, что по двум углам и то есть

Прямая пересекает две его стороны и продолжение третьей стороны

По теореме Менелая,

по углу и двум сторонам, отсюда

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Докажем, что — параллелограмм.

Тогда по углу и двум пропорциональным сторонам,

Это значит, что по углу и двум сторонам и

Получим, что в четырёхугольнике :

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

Тогда — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

Найдём из по теореме косинусов.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Проверим выполнение равенства

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Стереометрия. Страница 1

1. Основные фигуры стереометрии

Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом.

2. Группа дополнительных аксиом стереометрии

1. Для любой плоскости в пространстве, существуют точки принадлежащие данной плоскости и точки не принадлежащие ей.

2. Две различные плоскости, имеющие одну общую точку, пересекаются по прямой, проходящей через эту точку.

3. Через две различные прямые, имеющие общую точку, можно провести только одну плоскость.

Рис. 1. Аксиомы стереометрии.

Пример

Даны три попарно пересекающиеся плоскости. Две прямые пересечения из них пересекаются. Доказать, что три прямые пересечения этих плоскостей пересекаются в одной точке.

Пусть даны три попарно пересекающиеся плоскости α, β и γ. Плоскость α пересекает плоскость β по прямой а. А плоскость β пересекает плоскость γ по прямой с (Рис. 2 а).

точка Е ∈ а,с (прямые пересекаются в точке Е по условию задачи)

Тогда плоскости α и γ пересекаются по прямой b.

Отсюда следует, что, т.к. прямые b,с ∈ γ, то они либо параллельны, либо пересекаются в какой-то точке Е₁.

Если они параллельны, то у них нет общих точек, а следовательно, плоскости α и β пересекаются по прямой а, параллельной b и с (Рис. 2 б). А это противоречит условию задачи. Следовательно, прямые b и с пересекаются в какой-то точке Е₁.

Отсюда можно сделать вывод, что точка Е₁ принадлежит трем плоскостям α,β,γ и, следовательно, она лежит одновременно на трех прямых а, b и с. А это возможно только, если три прямые пересекаются в одной точке. И, следовательно, прямая b пересекает прямую с в точке Е₁, которая является точкой пересечения прямых а и с. Таким образом, точки Е и Е₁ совпадают.

Рис.2. Даны три попарно пересекающиеся плоскости.

3. Плоскость, проходящая через данную прямую и точку

Теорема: Через прямую и не лежащую на ней точку можно провести только одну плоскость.

Доказательство.

Пусть АВ данная прямая и Е не принадлежащая ей точка. (Рис.3) Проведем через точки А и Е прямую. Тогда прямые АВ и АЕ пересекаются в точке А. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость α, проведенная через эти прямые, единственная. Т.к. точка Е принадлежит прямой АЕ, то она принадлежит плоскости α.

Если допустить, что существует еще одна плоскость α’, проходящая через прямую АВ и точку Е, то эта плоскость пересекает плоскость α по прямой, на которой лежат точки А, В, и Е согласно аксиоме 2. А это противоречит условию, т.к. точки А, В, и Е не лежат на одной прямой. Следовательно, плоскость α единственная.

Рис. 3 Плоскость, проходящая через данную прямую и точку.

4. Пересечение прямой с плоскостью

Теорема: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит данной плоскости.

Доказательство.

Проведем через прямую а и точку С плоскость β. Тогда, если плоскости α и β совпадают, то прямая а принадлежит плоскости α, что и утверждает данная теорема. Если плоскости α и β не совпадают, то они пересекаются по прямой а’. Таким образом, имеем:

точки А и В ∈ а, α
прямая а ∈ β
следовательно, точки А и В ∈β

Отсюда следует, что две точки А и В принадлежат двум плоскостям: α и β. И, согласно аксиоме, они могут лежать только на прямой а’, которая является прямой пересечения этих плоскостей. Т.к. через две точки можно провести только одну прямую, и по условию теоремы эта прямая есть а, то следовательно, она и является прямой пересечения двух плоскостей. Т.е. прямые а и а’ совпадают. А следовательно, прямая а принадлежит плоскости α.

Из данной теоремы следует, что плоскость и не принадлежащая ей прямая, либо не пересекаются, либо пересекаются в одной точке.

Рис. 4 Пересечение прямой с плоскостью.

5. Существование плоскости, проходящей через три данные точки

Теорема. Через три точки, не лежащие на данной прямой, можно провести только одну плоскость. Рис.5

Доказательство. Пусть А, В, С три точки, не лежащие на одной прямой. Проведем через точки А,С и В,С прямые. Тогда они пересекаются в точке С. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость, проведенная через эти прямые, единственная. По теореме о пересечении прямой с плоскостью, обе прямые целиком принадлежат данной плоскости.

Рис. 5 Существование плоскости, проходящей через три данные точки.

6.Пример 1

Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Доказательство:

Пусть дана данная прямая а и точка О, не принадлежащая прямой а. И даны пересекающие ее прямые b, c, d в точках B, C, D, которые пересекаются в точке О. Проведем через прямую а и точку О плоскость α (Рис.6).

По теореме о пересечении прямой и плоскости, если провести прямую b, проходящую через точку О и точку В прямой а, то она целиком будет принадлежать плоскости α, так как две точки прямой b принадлежат плоскости α.

Если допустить, что прямая b не принадлежит плоскости α, то в этом случае мы можем провести плоскость α’, проходящую через точки В и О. Тогда плоскости α и α’ пересекаются по прямой b’, проходящей через точки В и О. А так как через две точки можно провести только одну прямую, то прямые b и b’ совпадают. Следовательно, прямая b целиком принадлежит плоскости α.

Точно так же доказывается, что прямые с и d принадлежат плоскости α. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Рис.6 Задача. Докажите, что все прямые, пересекающие данную прямую.

Пример 2

Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую.

Доказательство:

Пусть даны две непересекающиеся плоскости α и α’. И прямая а, которая пересекает плоскость α в точке В (Рис.7). Необходимо доказать, что прямая а пересекает плоскость α’ в точке В’.

Возьмем на плоскости α’ точку А и проведем через нее и прямую а плоскость β. Тогда плоскость β будет пересекать плоскости α и α’ по параллельным прямым b и b’. Точка В принадлежит прямой b, так как она принадлежит плоскости α и лежит на прямой а. И следовательно, она принадлежит двум плоскостям α и β.

Таким образом получается, что на плоскости β лежат две параллельные прямые b и b’. Одну из них пересекает прямая а в точке В. Следовательно, прямая а пересекает и вторую прямую b’. Так как согласно аксеоме, через точку В, не лежащей на данной прямой b’, можно провести только одну, параллельную прямой b’, прямую b. Отсюда следует, что прямая а не параллельна прямой b’, она ее пересекает в точке B’.

Рис.7 Задача. Даны две непересекающиеся плоскости.

Пример 3

Даны две плоскости, пересекающиеся по прямой а. И прямая b, которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые а и b пересекаются.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Прямая b лежит в плоскости β и пересекает плоскость α в точке А (Рис.8). Необходимо доказать, что прямая b пересекает прямую а.

По условию задачи, прямая b лежит в плоскости β и пересекает плоскость α в точке А. Следовательно, точка А принадлежит двум плоскостям α и β.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что, так как точка А принадлежит двум плоскостям, то она лежит на прямой а, потому что прямая а является прямой пересечения двух плоскостей α и β.

Таким образом, точка А принадлежит двум прямым а и b. А следовательно, эти прямые пересекаются.

Рис.8 Задача. Даны две плоскости, пересекающиеся по прямой а.

Пример 4

Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Точки А, В, С одновременно принадлежат двум плоскостям α и β (Рис.9). Необходимо доказать, что все три точки принадлежат прямой а.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что все три точки А, В и С лежат на прямой пересечения двух плоскостей, т.е. прямой а, так как они принадлежат обоим плоскостям α и β.

Пусть дана точка D, принадлежащая только плоскости β. Тогда она не может лежать на прямой а, так как она не принадлежит плоскости α. Точно так же точка Е не может принадлежать прямой а, так как она принадлежит только плоскости α. Точка F не принадлежит плоскостям α и β, а следовательно, и прямой а.

Рис.9 Задача. Точки А, В, С лежат в каждой из двух различных плоскостей.

Пример 5

Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.

Доказательство:

Пусть даны четыре точки А, В, С, D. Допустим, что все четыре точки лежат в одной плоскости α.

Прямая АВ не пересекается с прямой CD. Прямая АС также не пересекается с прямой BD. Если провести прямую AD, то точки В и С окажутся в разных полуплоскостях. Следовательно, прямая AD пересекается с прямой ВС в точке О (Рис.10 а).

Допустим, что прямая AB не пересекает прямую DС (Рис.10 б). АD не пересекает прямую BC. Тогда, если провести прямую АС, то точки B и D окажутся в разных полуплоскостях. И прямая АС будет пересекать прямую BD в точке О.

Теперь допустим, что прямая AC не пересекает прямую ВD (Рис.10 в). АD не пересекает прямую ВC. Тогда, если провести прямую АВ, то точки D и C окажутся в разны полуплоскостях. А следовательно, прямая АВ будет пересекать прямую СD в точке О.

Отсюда можно сделать вывод, для того, чтобы выполнялось условие, при котором прямые АВ, АС, АD, одновременно не пересекали бы прямые CD, BD, BC, необходимо чтобы четыре точки А, В, С и D лежали в разных плоскостях.

Рис.10 Задача. Даны четыре точки. Известно, что прямая.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

• ← как доказать что прямые параллельны в треугольнике
• как доказать что прямые скрещивающиеся →

Главная > Учебные материалы > Математика: Стереометрия. Страница 1