как доказать что треугольники равны 7 класс
Как установить и доказать, что треугольники равны
Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.
Как доказать, что треугольники равны
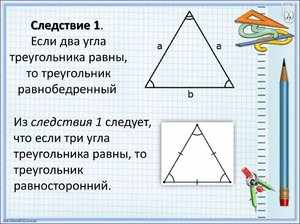
Чтобы доказать, что углы треугольников равны, помогут следующие варианты:
Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.
Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.
Признаки равенства треугольников
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
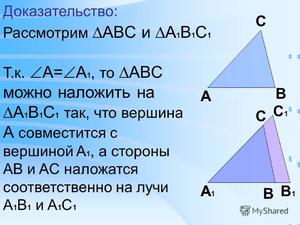
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Геометрия. 7 класс
Конспект урока
Решение задач на признаки равенства треугольников
Перечень рассматриваемых вопросов:
Теорема – это утверждение, справедливость которого устанавливается путём рассуждений в данной системе аксиом.
Стороны треугольника – отрезки, соединяющие вершины треугольника.
Равные треугольники – треугольники, которые можно совместить наложением.
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Теоретический материал для самостоятельного изучения
В предыдущих уроках были рассмотрены различные способы определения и доказательства равенства треугольников, такие как: способ наложения, признаки равенства треугольников.
Сегодня мы будем решать задачи на вычисления и доказательство равенства треугольников.
Для успешного понимания материалов урока вспомним, какие треугольники называются равными.
‑ Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.
‑ Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.
Повторим теоремы о равенстве треугольников, так называемые признаки равенства треугольников.
1) Первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2) Второй признак равенства треугольников.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3) Третий признак равенства треугольников.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Решим задачи, используя признаки равенства треугольников.
Отрезки AB и CD – диаметры окружности с центром в точке O. Найдите периметр треугольника AOD, если отрезок CB = 13 см, а отрезок AB = 18 см.
окружность с центром O;
1) ∆AOD = ∆OBC (по первому признаку равенства треугольников).
2) Т. к. AO = OB = OC = OD = 18:2 = 9 см (как радиусы окружностей); ∠AOD = ∠COB (т. к. вертикальные углы) → CB = AD = 13 см.
3) P∆AOD = AO + OD + AD = 9 + 9 +13 = 31 см
В четырёхугольнике ABCD, AB = CD, AD = CB, BE – биссектриса ∠B, DF – биссектриса ∠D.
Докажите, что ∠ABE = ∠ADF, ∆ABE = ∆CDF.
BE – биссектриса ∠B ∆ABС,
DF– биссектриса ∠D ∆CDА
1) ∆ABC = ∆ACD (по третьему признаку равенства треугольников).
2) Т. к. AC – общая сторона, AB = CD, AD = CB (по условию) →∠B = ∠D.
3) По условию BE – биссектриса ∠B ∆ABС, DF– биссектриса ∠D ∆CDА →∠B = ∠CBE +∠ABE = ∠ADF + ∠CDF = ∠D.
При этом ∠CBE = ∠ABE, ∠ADF = ∠CDF→∠B = 2∠ABE = 2∠ADF = ∠D→∠ABE = ∠ADF.
Т. к. AB = CD (по условию), ∠ABE = ∠ADF (доказано), ∠EAB = ∠CDF (т. к. ∆ABC = ∆ACD по третьему признаку равенства треугольников). Что и требовалось доказать.
Материал для углубленного изучения темы.
1) Приложим треугольник ∆ ABC к ∆ А1В1С1, так чтобы вершина A совместилась с вершиной A1, вершина B с B1, вершины C и C1 лежали по разные стороны от прямой A1B1.
2) Соединим точки C и C1, так чтобы получился треугольник CC1B.
3) Так как BC = B1C1, → ∆CC1B – равнобедренный, по теореме о свойстве углов равнобедренного треугольника, →∠C = ∠С1.
4) ∆CC1A – также равнобедренный (по теореме о свойстве углов равнобедренного треугольника) → ∠ CС1A = ∠С1CA → ∠ACB = ∠AС1B
Разбор заданий тренировочного модуля.
№ 1. На рисунке изображены треугольники ABD и BCD. По какому признаку, используя данные рисунка, можно доказать их равенство?
По рисунку видно, что ∠ADB = ∠DBC(углы отмечены двойной линией), ∠ABD = ∠BDC (углы отмечены одной линией), сторона DB – общая, следовательно, ∆ABD = ∆BCD (по второму признаку равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны).
Ответ: используя данные рисунка, можно доказать равенство треугольников, используя второй признак равенства треугольников.
№ 2. На рисунке CD = AB, O – центр окружности. Точки A, B, C, D лежат на окружности. CD = 17 см, CO = 15 см. Найдите периметр ∆AOB.
1) Так как по условию O – центр окружности и так как точки A, B, C, D лежат на окружности, то отрезки OA = OB = OD = OC = 15 см (как радиусы окружности). CD = AB = 17 см (по условию). Периметр ∆AOB – это сумма всех его сторон.
Р∆AOB = OA + OB + AB = 15 +15 + 17 = 47 см
Как доказать что треугольники равны 7 класс
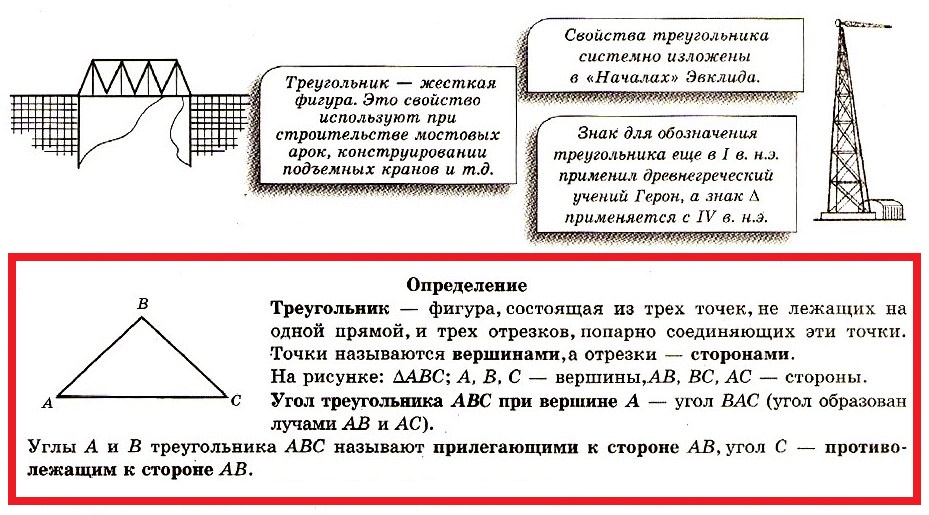
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.
Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.
Медиана, биссектриса и высота треугольника
Равные треугольники
Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.
Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.
Признаки равенства треугольников
Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.
Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:
Как установить и доказать, что треугольники равны
Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.
Как доказать, что треугольники равны
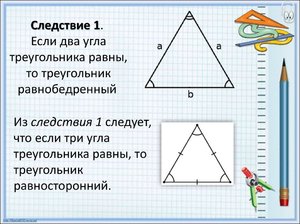
Чтобы доказать, что углы треугольников равны, помогут следующие варианты:
Это интересно: Как найти периметр треугольника.
3 признака равенства треугольников
Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.
Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.
Доказательство подобия треугольников
В рассмотрении темы подобия также приводятся 3 признака:
Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.
Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.