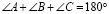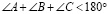как лобачевский доказал что параллельные прямые пересекаются

Геометрия Лобачевского

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Источник

Новое в блогах

Пересекаются ли параллельные или Что говорил Лобачевский?

Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.

Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.

Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:

«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!

Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.

Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.

Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.

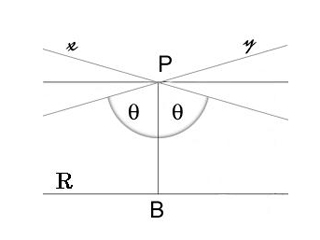
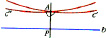
Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!

Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.

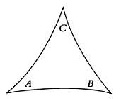
Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.

Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»

«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»

Источник

Пять мифов о геометрии Лобачевского

Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.

На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.

Миф второй. В теории Лобачевского параллельные прямые пересекаются

Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.

Миф четвертый. Геометрия Лобачевского не применима в реальной жизни

Миф пятый. Лобачевский первым создал неевклидову геометрию

Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.

Источник

Как лобачевский доказал что параллельные прямые пересекаются

В настоящее время геометрия широко применяется в самых разных областях: физике, химии, биологии и т.д. Неоценимо ее значение в прикладных науках: машиностроении, геодезии, картографии. Геометрия – часть нашей жизни. Но так было не всегда. Становлении геометрии как математической науки произошло позднее и связано с именами греческих ученых Фалеса (625 – 547 гг. до н.э.), Пифагора (580 – 500 гг. до н.э.), Демокрита (460 – 370 гг. до н.э.), Евклида (III век до н.э.) и др.

В знаменитом сочинении Евклида «Начала» был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). Сегодня мы используем большинство этих аксиом при решении задач. Много вопросов было по поводу пятого постулата, формулировку которого обычно заменяют аксиомой параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Много веков усилия большого числа ученых были направлены на доказательство данного утверждения, у некоторых математиков возникала мысль о невозможности доказательства пятого постулата. Решение этого вопроса было найдено великим русским математиком Николаем Ивановичем Лобачевским (1792—1856). Более того, он сделал замечательный вывод: можно построить другую геометрию, отличную от геометрии Евклида. И такая геометрия была построена – геометрия Лобачевского. Но возникает вопрос: после открытия геометрии Лобачевского применяется ли она в современной жизни? Ведь мало кто слышал о его геометрии, а если и слышал, то не знает истинного ее применения.

Объект исследования – геометрия Лобачевского.

Предмет исследования – применение геометрии Лобачевского в окружающем мире.

Цель исследования: изучить возможности применения геометрии Лобачевского в жизни.

Для достижения цели были поставлены следующие задачи:

– изучить и проанализировать учебную литературу, связанную с жизнью Лобачевского;

– ознакомиться с особенностями его теории;

– рассмотреть применение неевклидовой геометрии в современной жизни.

Была выдвинута гипотеза: применение геометрии Лобачевского не ограничивается математикой, она используется в других науках, в окружающем нас мире.

Мы использовали методы эмпирического уровня (наблюдение, опрос, фотографирование) и теоретического уровня (изучение, обобщение, анализ, абстрагирование).

1. Создание неевклидовой геометрии

Безуспешные поиски доказательства 5-го постулата сыграли ту положительную роль, что помогли глубже проникнуть в структуру геометрии, уяснить взаимную связь её важнейших предложений. Эти попытки подготовили почву для возникновения у передовых учёных предположения, что 5–ый постулат недоказуем при помощи остальных аксиом геометрии Евклида.

К открытию новой, так называемой «неевклидовой», геометрии пришли три человека:

1) профессор Казанского университета Николай Иванович Лобачевский (1792–1856);

2) великий немецкий математик Карл Фридрих Гаусс (1777–1855);

3) венгерский офицер Янош Бояи (1802–1860).

Однако вклад в создание новой геометрии, сделанный этими учёными, весьма неравноценен.

Что касается Гаусса, то он совершенно не оставил никаких следов систематического изложения своих открытий в области неевклидовой геометрии и при жизни не опубликовал ни одной строчки по этому вопросу. Гаусс слишком боялся уронить свой огромный авторитет в глазах учёного мира.

Янош Бояи пришёл к открытию неевклидовой геометрии в 1823 г., будучи в возрасте 21 года, но опубликовал свои результаты в 1832 г. (позже Лобачевского) в виде приложения к учебнику математики «Опыт введения учащегося юношества в начала чистой математики», изданному его отцом Ф. Бояи. Но, непонятый своими современниками, встретивший сдержанное, нечуткое отношение со стороны Гаусса, он впал в глубокое отчаяние. Больше ни одного произведения по новой геометрии Я. Бояи не опубликовал. Остаток жизни он трагически провёл в нужде, неизвестности и полном одиночестве, пережив и Гаусса, и Лобачевского.

Однако всё сделанное в области геометрии Гауссом и Я. Бояи представляет собой лишь первые шаги по сравнению с глубокими и далеко идущими исследованиями Лобачевского, который всю жизнь упорно и настойчиво разрабатывал с разных точек зрения своё учение, довёл его до высокой степени совершенства и опубликовал целый ряд крупных сочинений по новой геометрии. Поэтому как с формальной стороны (первое по времени опубликование открытия в 1826 г.), так и по существу первое место среди лиц, разделяющих славу создания неевклидовой геометрии, следует безраздельно отвести Н. И. Лобачевскому, имя которого и носит созданная им геометрия.

Геометрия Лобачевского так и не была понята и оценена при жизни самого учёного. Но уже через десятилетие после смерти Лобачевского его открытие привлекло всеобщее внимание математических кругов и послужило могучим стимулом к коренному пересмотру взглядов на основания геометрии.

Это объясняется тем, что к этому времени самим развитием математики была подготовлена почва к правильному восприятию и пониманию идей Лобачевского и к их дальнейшему углублению и развитию.

Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще.

2. Особенности геометрии Лобачевского

В геометрии Лобачевского вместо пятого постулата Евклида принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее.

Рассмотрим некоторые факты, отличающие данную геометрию от евклидовой.

В геометрии Лобачевского прямые на плоскости либо пересекаются, либо параллельны, либо являются расходящимися.

В геометрии Лобачевского сохраняются все теоремы, которые можно доказать без использования аксиомы параллельности.

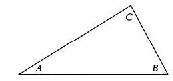
Теорема о сумме углов треугольника: сумма углов любого треугольника меньше 180°. При ее доказательстве используется аксиома параллельности.

Рис. 2. Геометрия Евклида

Рис. 3. Геометрия Лобачевского

Разность между 180° и суммой углов треугольника в геометрии Лобачевского называется дефектом этого треугольника. Площадь треугольника равна S = k ∙ D, где S – площадь, D – дефект треугольника, число k зависит от выбора единиц измерения площадей и углов и не зависит от выбранного треугольника. Площади треугольников в геометрии Лобачевского ограничены некоторой константой.

Согласно геометрии Евклида, если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. В геометрии Лобачевского нет подобных треугольников, но есть четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом, т. е. геометрическое место точек, удалённых от данной прямой на данное расстояние (в Евклидовой геометрии эквидистанта прямой есть прямая)

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность – предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растет быстрее.

Модели геометрии Лобачевского дали доказательство её непротиворечивости.

Рис. 5. Модель Пуанкаре

Рис. 6. Модель Клейна

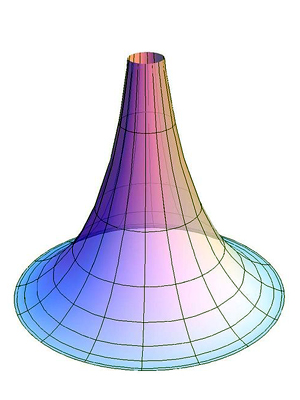
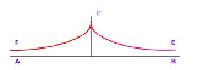
Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского сходна с геометрией на поверхностях постоянной отрицательной кривизны (псевдосфере). …Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере. Но эта модель является интерпретацией геометрии, неспособной отобразить всю плоскость Лобачевского.

Псевдосфера образуется вращением линии FСЕ, называемой трактриссой, вокруг её оси АВ.

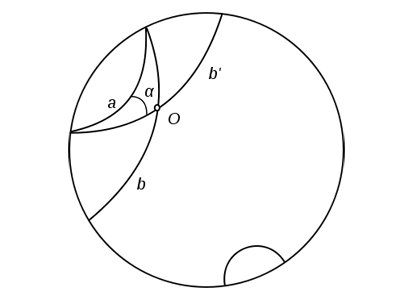
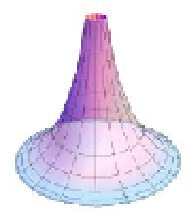
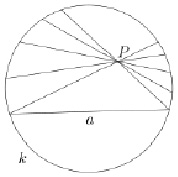
В модели Пуанкаре в круге за плоскость Лобачевского принимается внутренность круга в евклидовом пространстве; граница данного круга (окружность) называется «абсолютом». Роль геодезических прямых выполняют содержащиеся в этом круге дуги окружностей (a,b,b’), перпендикулярных абсолюту, и его диаметры.

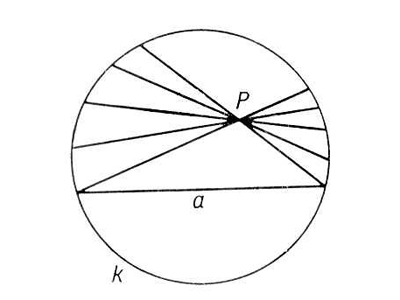
В 1871 году Клейном была создана первая полноценная модель плоскости Лобачевского. Плоскость – внутренность круга, прямая – хорда круга без концов, а точкой – точка внутри круга. «Движение» – любое преобразование круга в самого себя, переводящее хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Любое утверждение геометрии Лобачевского на плоскости – есть утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь не выполняется, так как через точку P, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых»).

Широко распространено заблуждение (отражённое, в частности, в нематематической литературе и фольклоре), что в геометрии Лобачевского параллельные прямые пересекаются. Во-первых, параллельные прямые не могут пересекаться (ни в одной геометрии) по определению параллельности. Во-вторых, в геометрии Лобачевского как раз можно провести через точку, не лежащую на данной прямой, бесконечно много прямых, не пересекающихся с ней.

Различия между геометрией Лобачевского и геометрией Евклида кроются в понимании самой природы пространства. Физическое трехмерное пространство искривлено, и лишь в бесконечно малых областях его можно считать плоским, евклидовым.

В наших земных пределах этой кривизной можно пренебречь и пользоваться положениями и теоремами евклидовой геометрии, а при измерении космических расстояний верны теоремы геометрии Лобачевского.

4. Применение неевклидовой геометрии в жизни

Важное практическое приложение геометрии Лобачевского нашел русский физик Александр Фридман. Используя в 1922 году идеи теории относительности и решая уравнение Эйнштейна, он пришел к выводу, что Вселенная расширяется с течением времени. Вскоре эта теория блестяще подтвердилась на практике, но уже, как это часто бывает, после смерти Фридмана. Наблюдения американского астронома Эдвина Хаббла подтвердили это. В 1929 году он, не знакомый с теорией Фридмана, обнаружил, что удаленные туманности как бы «разбегаются» в разные стороны. При этом скорость этого «разбегания» оказалась пропорциональна расстоянию между ними. Законы сложения относительных скоростей, полученные Альбертом Эйнштейном, напрямую связаны с геометрией Лобачевского. Эта связь основана на том, что равенство, выражающее закон распространения света x2 + y2 + z2 = c2t2 при делении на t2, даёт 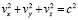– уравнение сферы в пространстве с координатами vx, vy, vz – составляющими скорости по осям х, у, z (в «пространстве скоростей»). А в1950-х годах советский физик Н.А. Черников стал успешно использовать геометрию Лобачевского для исследования столкновений элементарных частиц в ускорителе, а также при изучении других вопросов физики элементарных частиц и ядерных реакций.

Сам Лобачевский применял неевклидову геометрию для вычисления определенных интегралов при нахождении длины, площади или объема фигуры в своей геометрии. Но применение новых знаний не ограничилось математикой.

Также геометрия Лобачевского используется в астрономии: при описании голографической Вселенной или черных дыр.

Интересно применение в игровой индустрии: игра «Жизнь» (модель зарождения жизни во «Вселенной») или HyperRogue (гибрид паззла и рогалика на гиперболической плоскости). Одной из ее главных особенностей является уникальная игровая геометрия, необычная реализация миров, созданных на гиперболической плоскости, состоящей из шести и семиугольников. При создании игрового мира использовалась система неевклидовой геометрии, где сумма углов треугольника всегда меньше 180°.

Применяется геометрия Лобачевского в живописи. В 2013 году в московском Музее современного искусства прошла выставка Маурица Корнелиса Эшера. Нидерландский художник-график известен благодаря своим работам, где он использует различные математические понятия, приемы и теории: пределы, ленты Мебиуса, геометрию Лобачевского. Заинтересовали работы-иллюзии и орнаменты. Самые знаменитые работы Эшера построены как визуальные обманки, но по сути являются визуальным воплощением неевклидова пространства. Эшер не доказывал теорем с помощью своих рисунков, просто демонстрировал удивительные возможности нашего восприятия. Один из интересных примеров проявления неевклидовой геометрии в работах Эшера – «Картинная галерея». Еще один пример неевклидового пространства в работах Эшера – гравюра «Относительность».

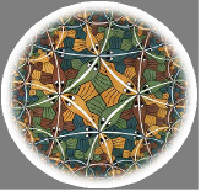
Один из примеров можно увидеть в работе «Предел круга III». Здесь представлена одна из моделей геометрии Лобачевского (модель Пуанкаре).

Рис. 7 «Относительность»

Рис. 8. «Предел круга III»

В 2015 году в Центральном зале центра дизайна ARTPLAY прошла еще одна не менее интересная выставка «Ван Гог. Ожившие полотна (Van Gogh Alive)». На его картинах отсутствует ровный фон, геометрия вангоговского пространства подчиняется законам, которые только предстояло открыть учёным 19-го столетия.

Использование геометрии Лобачевского в искусстве не ограничивается живописью.

Творчество Фрэнка Гери тому доказательство. Он продемонстрировал возможности современных технологий проектирования. Деконструктивизм и теория нелинейной архитектуры подчиняются формулам геометрии Лобачевского. Его здания похожи друг на друга словно детали «конструктора из титана», но «мнет и гнет» он их каждый раз по-другому. В этом заключается уникальность дизайна построенных объектов.

Рис. 9. Архитектура в Лос-Анджелесе

Рис. 10. Музей в г. Сидней

Мы вдохновились идеями Ф. Гери, поэтому решила найти элементы геометрии Лобачевского в архитектуре других стран.

Рис.12. Музей Гуггейнхейма в Испании

Рис. 13. Многофункциональный комплекс в Китае

Мы выяснили, что еще один архитектор в своем творчестве подчинялся законам неевклидовой геометрии. С помощью фоторедактора художник превращает городские здания в футуристическую архитектуру. Эти «Городские портреты» – маленький виртуальный мир Виктора Энрича, в котором нет никаких ограничений для фантазии.

В реальном мире тоже можно легко найти модели гиперболических поверхностей. Не стоит далеко ходить, достаточно рассмотреть в качестве гиперболической поверхности седло для верховой езды. Сумма углов любого треугольника, нарисованного на такой поверхности, составляет менее 180°, и параллельные линии здесь не находятся друг от друга на фиксированном расстоянии, а постепенно расходятся.

В обычной спальне я провел небольшой эксперимент, чтобы понаблюдать, как в гиперболическом мире движутся различные предметы. Нам потребовалась кровать с ровной поверхностью, как на евклидовой плоскости. На нее мы поставили подвижный объект (см. рисунок ниже). Рядом с ним положила тяжелый предмет, так чтобы постель прогнулась. Теперь поверхность уже не является плоской, она искривилась. Из-за этой кривизны подвижный объект будет скользить к тяжелому предмету. Поверхность постели вокруг тяжелого предмета похожа на гиперболическую поверхность.

Гиперболические пространства (т.е. пространства, в которых действуют законы гиперболической геометрии) встречаются и в самой природе. Например: Геометрия Лобачевского проглядывается в структурах кораллов, в организации клеточных структур у растении, у некоторых цветков.

А вот профессор Университета Корнелла в Нью-Йорке Дайна Тайминя разрешила столетнюю проблему неевклидовой геометрии по визуализации гиперболических плоскостей. Свою первую модель гиперболической плоскости она связала крючком в 1997 году, чтобы использовать в студийном курсе неевклидовой геометрии. С тех пор она связала более сотни геометрических моделей. На данный момент она имеет признание на международном уровне из-за того, что благодаря ее необычному открытию, что модель гиперболической плоскости, которую нельзя изготовить даже с помощью компьютера, возможно сделать, используя вязание крючком. Красивые, математически описываемые сложными формулами модели, похожие на жителей морских глубин.

Рис. 17. Листья салата

Изучив литературу по данному вопросы, мы задумали провести опрос среди 9–11 классов: насколько же эрудированны в данной области наши ровесники?

Большинство обучающихся знают, кем был Н.И. Лобачевский, чем отличается его геометрия от привычной нам евклидовой, где ее можно применять. Применение геометрии Лобачевского не ограничивается одной математикой, существуют и другие области ее применения. Благодаря зрительным искажениям, существует искусство (живопись, архитектура). Но одних наблюдений недостаточно, необходимо опираться на доказательства. «Новая», неевклидова геометрия открывает широкие возможности различным направлениям наук.

Заключение

Геометрия Лобачевского – геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется на аксиому о параллельных Лобачевского. Данная теория совершенно верна, если ее рассматривать не на плоскости, а на поверхности вогнутой поверхности, напоминающей седло (гиперболического параболоида).

• мы изучили учебную литературу, связанную с жизнью Лобачевского;

• познакомились с особенностями его теории;

• рассмотрели применение неевклидовой геометрии в современной жизни. Сам Лобачевский пытался рассмотреть свою теорию в рамках геометрии (пятого постулата), но другие области нашей жизни активно используют положения его теории. Это и физика, и астрономия, и искусство (живопись и архитектура), и игровая индустрия. Задача современного человека – повышение уровня своего образования, изучать новое и видеть применение полученных знаний. Надеюсь, что учащиеся, услышав о геометрии Лобачевского, заинтересуются этим вопросом, оглянутся вокруг, смогут объяснить какие-либо явления, а возможно, и сделают открытие.

Таким образом, цель работы достигнута, задачи выполнены, гипотеза подтверждена.

1. Слышали ли вы фамилию Лобачевский? Кем он был?

2. В чем отличие геометрии Лобачевского от геометрии Евклида?

3. Где можно применить неевклидову геометрию?

4. Как расположены буквы на картинке: параллельно (стоят прямо) или нет?

5. Что изображено на картинке: спираль или несколько окружностей?

Источник