как определяется вектор электрического смещения что он характеризует
Как определяется вектор электрического смещения что он характеризует
Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами, так что вектор напряженности E, характеризующий результирующее поле в диэлектрике,
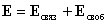
Если обозначить объемную плотность свободных зарядов 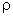
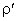
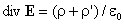
в дифференциальной форме, либо в интегральной форме
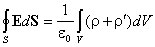
С учетом выражения (2.1)
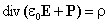
откуда для вектора электрического смещения (индукции) находим
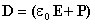
Последнее выражение показывает, что вектор электрической индукции учитывает поляризованность среды. Возвращаясь к соответствующим формулировкам теоремы Гаусса
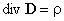
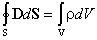
можно видеть, что вектор электрического смещения характеризует источники электрического поля, т. е. свободные заряды, на которых этот вектор начинается и заканчивается. Так как 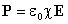
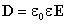
Напряженность электрического поля характеризует как свободные, так и связанные заряды, поэтому вектор напряженности терпит разрывы на границах областей, где присутствуют связанные заряды, например на границе раздела двух диэлектриков с различными 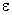
1) Как определяется вектор электрического смещения. Каково его направление
2) В некоторой точке изотропного диэлектрика с проницаемостью смещение имеет значение D. Чему равна поляризованность P в этой точке
3) Чему равен поток вектора электрического смещения через замкнутую поверхность в электрическом поле
Вектор электрического смещения
Электрическое поле графически изображается системой линий напряженности. На границе раздела двух диэлектриков количество линий напряженности изменяется: часть их заканчивается или начинается на связанных зарядах (рис. 47.1). По этой причине для описания поля в неоднородных диэлектриках используется вспомогательная величина – вектор электрического смещения

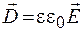
Направление вектора смещения в изотропной среде совпадает с направлением вектора напряженности. Линии вектора смещения непрерывны на границе раздела различных диэлектриков (рис. 47.2).
Объединяя выражения (47.1) и (29.2), для поля плоского конденсатора получаем
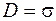
Следовательно, единицей вектора электрического смещения является кулон на метр в квадрате 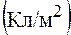
Поток вектора электрического смещения через поверхность S определяется формулой
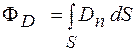
Из выражения теоремы Гаусса для напряженности электрического поля можно получить соответству-ющее выражение для вектора электрического смещения. Умножив обе части уравнения (26.7) на 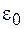
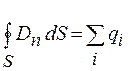
Поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности.
Для установления связи между вектором электрического смещения и поляризованностью диэлектрика подставим выражение (46.7) в уравнение (47.1):
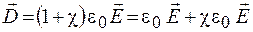
Учитывая выражение (45.3), формулу (47.5) приводим к виду
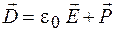
В вакууме (практически и в воздухе) 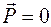
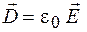
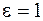
Таким образом, для описания электрических полей кроме напряженности 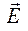


Дата добавления: 2015-08-08 ; просмотров: 5778 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
3.4. Вектор электрического смещения
Разобравшись с поведением диэлектрика на микроскопическом уровне, вернемся к плоскому конденсатору, изображенному на рис. 3.3. Откуда же взялись поляризационные заряды на поверхности диэлектрической пластины между обкладками?
Теперь мы знаем, что во внешнем поле, создаваемом обкладками, единица объема диэлектрика приобретает дипольный момент Р. Скажем, положительные заряды смещаются по направлению поля (вверх на рис. 3.3), а отрицательные — вниз. При полной однородности поля и диэлектрика объемные нескомпенсированные заряды внутри диэлектрика не появляются. Но такой сдвиг приводит к возникновению нескомпенсированных зарядов на поверхности диэлектрической пластины. Дипольный момент пластины равен VР, где V = Sd — ее объем. С другой стороны, полный поверхностный заряд на пластине равен
а расстояние между центрами положительных и отрицательных зарядов равно d (см. рис. 3.3). Поэтому дипольный момент пластины можно также записать как
Сравнивая эти два выражения, находим связь поверхностной плотности поляризационных зарядов с вектором поляризации
Напряженность Е суммарного поля внутри диэлектрика меньше напряженности поля E0, создаваемого обкладками. Именно поле Е действует на молекулы диэлектрика, именно его они «чувствуют», и потому для него справедливо соотношение (3.22)
Используя связь (3.3) напряженности поля Е ‘ поляризационных зарядов с суммарным полем Е
мы находим связь между диэлектрической проницаемостью и диэлектрической восприимчивостью
В общем случае вектор поляризации Р не параллелен вектору напряженности суммарного поля Е: в анизотропных диэлектриках вектор поляризации может поворачиваться относительно напряженности поля. Однако всегда мы можем записать соотношение
называется вектором электрического смещения (вектором электрической индукции).
В частном случае линейной зависимости поляризации от напряженности поля
вектор электрического смещения равен
где 
имеет место для изотропных диэлектриков. В общем случае вектор D не параллелен Е. Поле вектора D можно графически изобразить линиями электрического смещения, которые определяются так же, как и линии напряженности электрического поля (рис 3.23 и 3.24).
Рис. 3.23. Условия на плоской границе двух диэлектриков для напряженности и электрического смещения
Рис. 3.24. Линии напряженности и электрического смещения электрического поля
от точечного заряда, расположенного на границе раздела двух диэлектриков
В СИ единицей измерения электрического смещения является:
Вектор электрического смещения, восприимчивость и диэлектрическая проницаемость. Теорема Гаусса для векторов P и D.



Напряженность электростатического поля, зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле ещевектором электрического смещения, который для электрически изотропной среды, по определению, равен 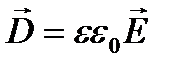
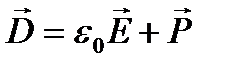
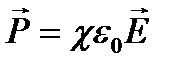
ε=æ+1. ε показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.
Единица электрического смещения — кулон на метр в квадрате (Кл/м 2 ). Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Аналогично, как и поле Е, поле D изображается с помощьюлиний электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность
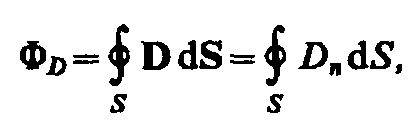
Теорема Гаусса дляэлектростатического поля в диэлектрике:
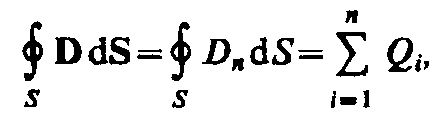
Для вакуума Dn = e0En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность равен
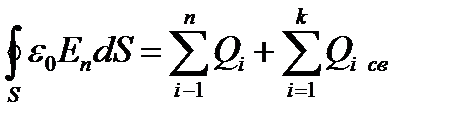
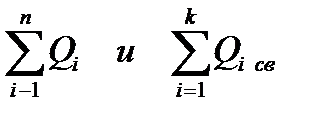
Вектор электрической индукции
Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :
Вектор электрического смещения в СНС определяется как:
Вектор индукции
Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:
Связь вектора напряженности и вектора электрического смещения
При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:
Где ε – диэлектическая проницаемость среды.
Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:
Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:
Формула тангенциальной составляющей:
Поле вектора D → изображается при помощи линий электрического смещения.
Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.
Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:
Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:
Запись результирующего поля с диэлектриком примет вид:
Формула плотности связанных зарядов:
Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:
Ответ: вектор электрической индукции не изменяется.
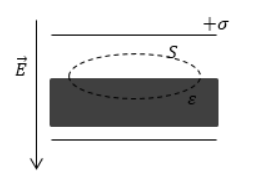
Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.
Рисунок 1 . Замкнутая поверхность
Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :
Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.
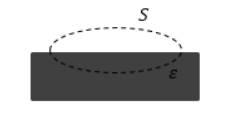
Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика
Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:
Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:
Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.
Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.