как по радиусу узнать площадь
Площадь круга: как найти, формулы
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как глобус и мяч.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
Площадь круга через диаметр
S = π × d 2 : 4, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
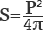
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Как найти площадь круга
Окружность — одна из самых совершенных фигур в геометрии. Построить ее очень просто — нужен только циркуль. Но при своем совершенстве окружность создает одну из самых сложных проблем — определение площади круга. Почему это является проблемой? Дело в том, что площадь измеряется в квадратных единицах (метрах, дециметрах, миллиметрах…). Но превратить круг в прямоугольник или квадрат практически невозможно. Задача эта беспокоила умы математиков и философов на протяжении тысячелетий и даже получала собственное название — квадратура круга.
Чтобы разобраться в проблеме нужно разделить понятия окружности и круга. Окружность — это замкнутая линия, все точки которой находятся на одинаковом расстоянии от центра. А круг — это часть плоскости, ограниченная этой окружностью. Для окружности мы ищем длину, а для круга — площадь. Какую бы часть круга, ограниченную окружностью, мы не выбрали, одна из сторон обязательно будет криволинейной. Это усложняет расчет площади, если не использовать интегрального исчисления.
Приблизительно, с высокой долей точности можно найти площадь окружности через диаметр по формуле:
Это самая простая формула, позволяющая найти площадь круга, когда известный радиус. Но может возникнуть вопрос, почему найденная площадь будет неточной? Сложность связана с числом π — это отношение длины окружности к диаметру, не имеющая конечного значения. Такие числа называют иррациональными. Еще в 1761 году Иоганн Ламберт доказал, что эта постоянная трансцендентная, то есть, если возвести ее в квадрат, все равно получится иррациональное число.
Сложное доказательство этого утверждения создали Феликс Клейн и профессор Линдеманн. Практическое значение этого открытия состоит в том, что любая формула для определения площади круга, где используется число π дает приблизительный результат, то есть, квадратура круга невозможна в принципе. На данный момент известно число «Пи» с точностью до 31, 4 триллиона знаков после запятой. Для вычислений используют значение 3, 14, а для более точных — 3, 1415926.
Способы вычисления площади круга
Для решения повседневных и большинство технических задач вполне достаточно формулы S= π∙ D 2 /4. Но в геометрии есть свои подходы к решению. Не всегда дано радиус (диаметр), а измерить эту величину можно только косвенным путем при помощи построений описанных и вписанных многоугольников, дополнительных построений и т.д. Рассмотрим наиболее популярные методы, как узнать площадь круга, более подробно. Сразу же оговоримся, способ интегрального исчисления затрагивать не будем, хотя он и наиболее точный. Воспользуемся только геометрическими способами решения.
Вычисление площади по радиусу
S = π∙r 2 — формула для вычисления площади круга, если известный радиус. Как видно, это просто запись предыдущего выражения с учетом того, что r = D/2, отсюда r 2 = (D/2) 2 = D 2 /4, что и использовано в основной формуле.
Как найти площадь круга через длину окружности
Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:
R=L/2 π; (1)
D=L/ π. (2)
Используя запись 1 в формуле S = π∙r2 получаем:
S = π(L/2 π) 2 = L/4 π.
Аналогичный результат получим, используя формулу 2.
Как вычислить площадь круга, описанного вокруг правильного многоугольника
В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:
S=2π⋅a 2 /2, где а – сторона квадрата.
Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:
S=π⋅a 2 /3.
Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:
Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:
S=π⋅( a 4 /4⋅a 2 −b 2 )
В случае прямоугольного треугольника, мы используем формулу:
S=π/4⋅(a 2 +b 2 ).
Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:
S=π⋅( a⋅d⋅c/4⋅√p⋅(p−a)⋅(p−d)⋅(p−c)).
Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:
S=π⋅a 2 /12 – для равностороннего треугольника;
S=π⋅b 2 /4 ⋅(tgα/2) 2 — для равнобедренной трапеции;
S=π⋅(а/2) 2 =π⋅а 2 /4 — для квадрата.
Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.
Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:
S = π∙r 2 /2, или
S= π∙ D 2 /4/2 = S= π∙ D 2 /8.
Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах. Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний.
Площадь круга
Существует несколько формул для нахождения площади круга. На нашем сайте мы предлагаем вам расчет по трем формулам. В зависимости от исходных данных, площадь круга можно найти через:
Круг — множество точек плоскости, удаленных от заданной точки этой плоскости (эту точку называют центр круга) на расстояние, не превышающее заданное (это расстояние — радиус круга).
Площадь круга онлайн калькулятор
Площадь круга через радиус
Чтобы найти площадь круга, зная его радиус, необходимо воспользоваться формулой:
S= \pi r^2
В этой формуле r — радиус круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через диаметр
Диаметр — отрезок, проходящий через центр окружности и соединяющий две точки на окружности. Диаметр равен двум радиусам.
Если известен диаметр круга, то его площадь можно найти по формуле:
S= \dfrac<\pi><4>d^2
Здесь d — диаметр круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через длину окружности
Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг.
В случае, когда известна длина окружности, площадь круга можно рассчитать по следующей формуле:
S= \dfrac
Здесь l — длина окружности, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. 
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 

После того, как найдем диагональ – мы сможем рассчитать радиус: 
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.






