как понять что треугольник тупоугольный по сторонам
Тупоугольный треугольник, элементы, свойства, признаки и формулы
Тупоугольный треугольник, элементы, свойства, признаки и формулы.
Тупоугольный треугольник – это треугольник, у которого один угол тупой.
Тупоугольный треугольник (понятие и определение):
Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.
Рис. 1. Тупоугольный треугольник
∠ BАC– тупой угол треугольника,
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
Рис. 3. Прямоугольный треугольник
Рис. 4. Равнобедренный треугольник
АВ = AС – боковые стороны, BС – основание,
Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы тупоугольного треугольника:
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.
Рис. 5. Тупоугольный треугольник и внешний угол
Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника
MA – медиана тупоугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника
MС – высота тупоугольного треугольника
Высота тупоугольного треугольника может лежать за пределами треугольника.
Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника
MA – биссектриса тупого угла тупоугольного треугольника
Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
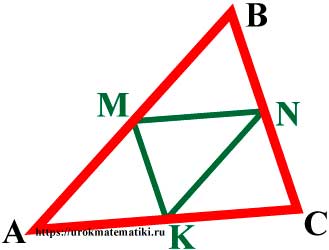
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
Треугольник и его виды. Элементы треугольника
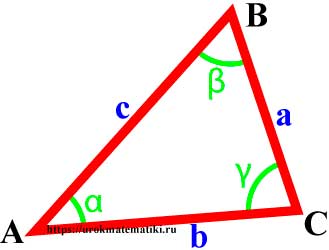
Треугольник – это геометрическая фигура, состоящая из трех точек, попарно соединенных между собой отрезками. Точки называются вершинами треугольника, отрезки – сторонами треугольника. Треугольник имеет три вершины и три стороны. Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
Внутренние углы треугольника – это углы, образованные его сторонами. Угол А – это угол, образованный сторонами АВ и АС.
Виды треугольников по углам:
Виды треугольников по сторонам:
Элементы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.
Биссектриса – это отрезок, делящий угол треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке.
Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке, называемой ортоцентром треугольника.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Серединный перпендикуляр к отрезку – прямая, перпендикулярная к этому отрезку и проходящая через его середину. Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.
Основные свойства треугольников
Внутренние углы треугольника относятся как 3:7:8. Найдите отношение внешних углов треугольника.
Чему равна градусная мера одного из углов прямоугольного треугольника?
Если в треугольнике один угол больше суммы двух других углов, то он
Если в треугольнике один внешний угол острый, то этот треугольник
Периметр равнобедренного треугольника равен 11 см, а основание равно 3 см. Найдите боковую сторону треугольника.
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
Остроугольный треугольник
— все углы треугольника острые.
Тупоугольный треугольник
— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник
— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник
Равносторонний (правильный) треугольник
— все три стороны равны.
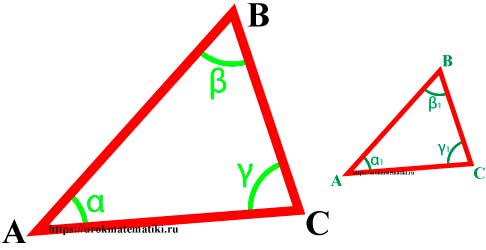
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
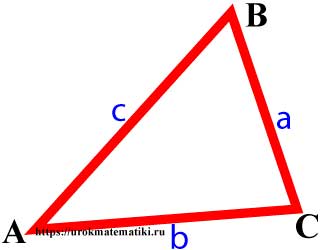
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
a sin α = b sin β = c sin γ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
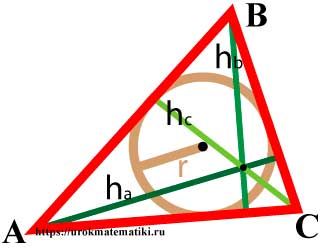
Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника
S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE
Формулы медиан треугольника
Формулы медиан треугольника через стороны
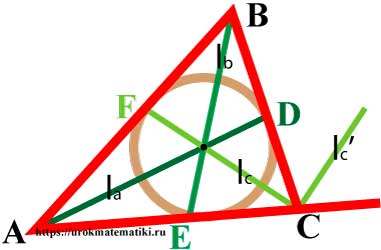
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника
Угол между l c и l c ‘ = 90°
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
где p = a + b + c 2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
l a = 2 b c cos α 2 b + c
l b = 2 a c cos β 2 a + c
l c = 2 a b cos γ 2 a + b
Высоты треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
Свойства высот треугольника
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
h a = b sin γ = c sin β
h b = c sin α = a sin γ
h c = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
Формулы высот треугольника через две стороны и радиус описанной окружности
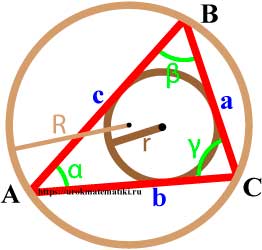
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
Радиус вписанной в треугольник окружности через три стороны
Формулы высот треугольника через две стороны и радиус описанной окружности
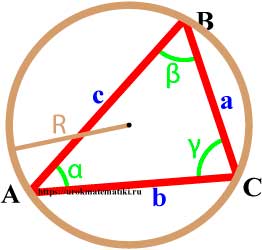
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
Радиус описанной окружности через площадь и три угла
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
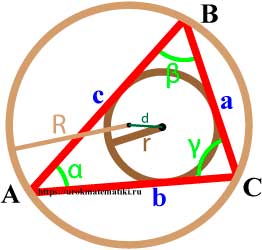
Связь между вписанной и описанной окружностями треугольника
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
Радиус описанной окружности через площадь и три угла
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
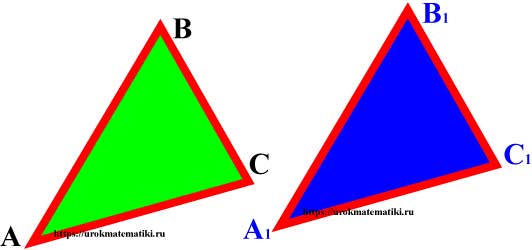
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
где k — коэффициент подобия.
Признаки подобия треугольников
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∡A — прямой, ∡B = 30°, и значит, что ∡C = 60°.
Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия: