как проверить в паскале что число простое
Определить простое число или нет
Нужно определить простое число или нет
Помогите кто может написать программу, которая могла бы определить простое число или нет (что бы.
Определить введенное число простое или составное
Определить введенное число простое или составное. Очень нужна. Можно на мыло jiehuh-das@ya.ru

Вообщем вот задание, не понятен только 1 пункт, он отмечен жирным. Вводится последовательность.

Напишите программу, запрашиваемую число и дающее заключение введенное число кратно 3 или нет. И все.
Решение
Решение
Coffy, мало того, что НЕ максимально быстрая и лёгкая, так ещё и неверная. Пожалуйста, старайтесь проверять код перед тем, как выкладывать его на всеобщее обозрение.
Вычисление trunc(sqrt(a))) на каждой итерации скорости явно не добавляет, не находите? Лучше вычислить это значение один раз перед циклом.
Если в цикле было выяснено, что число составное, незачем проверять все числа до trunc(sqrt(a))), можно досрочно выйти из цикла.
Вот, почитайте тему: Алгоритм, который устанавливает – является ли число простым. Хотя, это тоже далеко не максимально простое и максимально лёгкое.

Напишите пожалуйста программу по такому условию: Логической переменной присвоить TRUE или FALSE в.
Определить в тексте цифры и узнать число сост. из них симетрично или нет?
Задача такова: Программа должна определить есть ли в этом наборе символы соответсвующие десятичным.

Дано простое число. Составить функцию, которая находит следующее за ним простое число.
Дано простое число. Найти следующее за ним простое число
Дано простое число. Составить программу,которая будет находить следующее за ним простое.
Как определить простое число
Подпишись на новости, чтобы ничего не пропустить
Условие задачи 2.30
Задача 2.30
Дан одномерный массив А, состоящий из натуральных чисел. Вывести на экран количество простых чисел в массиве.
Для начала напомню, что такое простые числа.
То есть если число делится без остатка только на 1 и на самого себя, то такое число является простым.
Например, простыми числами являются 2, 3, 5 и т.п.
А вот 4 уже не является простым, так как делится без остатка не только на 1 и 4, но ещё и на 2.
Если вы подзабыли, что такое натуральное число, то см. здесь.
Как определить простое число в Паскале
Алгоритм решения с подробным разбором приведу на Паскале. Решение на С++ можете посмотреть в примере программы на С++.
ВАЖНО!
На этом многие могут ошибиться. В определении сказано, что простое число имеет ровно два различных делителя. Следовательно, число 1 не является простым (также не является простым, так как ноль можно делить на любые числа).
Проверять, является ли число простым, будем с помощью функции, которую сами и создадим. Эта функция будет возвращать TRUE, если число простое.
В функции сначала будем проверять, не является ли число меньше двух. Если да, то это уже не простое число. Если же число равно 2 или 3, то оно является однозначно простым и делать какие-то дополнительные проверки не требуется.
А вот если число N будет больше трёх, то в этом случае в цикле будем перебирать все возможные делители, начиная от 2 до (N-1). Если на какой-то делитель число N делится без остатка, значит, это тоже не простое число. В этом случае мы прерываем цикл (потому что проверять дальше нет смысла), а функция возвращает FALSE.
Проверять, делится ли число на самоё себя нет смысла (поэтому цикл длится только до N-1).
Алгоритмы нахождения простых чисел
Простые числа – это натуральные числа, большие единицы, которые имеют только два делителя: единицу и само это число.
(Единица не является простым числом!)
Существует множество задач, связанных с простыми числами, и хотя формулируются они достаточно просто, решить их бывает очень трудно. Некоторые свойства простых чисел еще не открыты. Это побудило немецкого математика Германа Вейля (Wayl, 1885-1955) так охарактеризовать простые числа: «Простые числа – это такие существа, которые всегда склонны прятаться от исследователя».
Во все времена люди хотели найти как можно большее простое число. Пока люди считали только при помощи карандаша и бумаги, им нечасто удавалось обнаружить новые простые числа. До 1952 г. самое большое известное простое число состояло из 39 цифр. Теперь поиском все больших простых чисел занимаются компьютеры. Это может представлять интерес для любителей рекордов.
Не будем гнаться за рекордами, а рассмотрим несколько алгоритмов нахождения простых чисел.
Задача 1. Определение простого числа.
Составить программу, которая будет проверять, является ли введенное число простым.
Самый простой путь решения этой задачи – проверить, имеет ли данное число n (n >= 2) делители в интервале [2; n-1]. Если делители есть, число n – составное, если – нет, то – простое. При реализации алгоритма разумно делать проверку на четность введенного числа, поскольку все четные числа делятся на 2 и являются составными числами, то, очевидно, что нет необходимости искать делители для этих чисел. Логическая переменная flag в программе выступает в роли “флаговой” переменной и повышает наглядность программы, так, если flag = true, то n –простое число; если у числа n есть делители, то “флаг выключаем” с помощью оператора присваивания flag:= false, таким образом, если flag = false, то n – составное число.
Задача 2. Нахождение простых чисел в заданном интервале.
Составить программу, которая напечатает все простые числа в заданном интервале [2, m], для m>3 и подсчитает их количество.
Будем использовать следующие приемы оптимизации алгоритма:
Как правило, учащиеся сами догадываются о приемах №1 и №3, но не всегда знают, как реализовать в программе досрочное завершение цикла, прием же №2 для них не очевиден, поэтому, возможно, учителю следует остановиться на нем более подробно или же привести полное доказательство этого утверждения.
Счетчик чисел будет находиться в переменной k. Когда очередное простое число найдено, он увеличивается на 1. Простые числа выводятся по 10 в строке, как только значение счетчика становится кратным 10, курсор переводится на новую строку.
Близнецы
Два нечетных простых числа, разнящихся на два, называются близнецами. Близнецами являются, например, числа 5 и 7, 11 и 13, 17 и 19 и т.д. В начале натурального ряда такие пары чисел встречаются достаточно часто, но, по мере того как мы продвигаемся в область больших чисел, их становится все меньше и меньше. Известно, что в первой сотне имеется целых 8 близнецов, дальше они расположены очень неравномерно, их можно обнаружить все реже и реже, гораздо реже, нежели сами простые числа. До сих пор неясно, конечно ли число близнецов. Более того, еще не найден способ, посредством которого можно было бы разрешить эту проблему.
Задача 3. Поиск пар чисел близнецов.
Написать программу, которая будет находить все числа близнецы в интервале [2; 1000] и подсчитывать количество пар чисел близнецов.
Фактически будем использовать алгоритм и программу Задачи 2. В этом алгоритме нужно использовать дополнительные переменные для хранения двух “последних” простых чисел и проверять условие наличия близнецов – их разность должна быть равна двум.
Задача 4. Нахождение простых чисел в заданном интервале с выводом в выходной файл.
Реализовать алгоритм задачи 2 с выводом простых чисел в выходной файл по 10 в строке. Последняя строка файла должна содержать информацию о количестве простых чисел в заданном интервале.
Задача 5. Приемы оптимизации алгоритма задачи 4.
Оптимизировать алгоритм задачи 4 следующим образом: найденные простые числа записывать в файл, делимость очередного кандидата проверять только на числа из этого файла.
Словесное описание алгоритма:
Эратосфеново решето
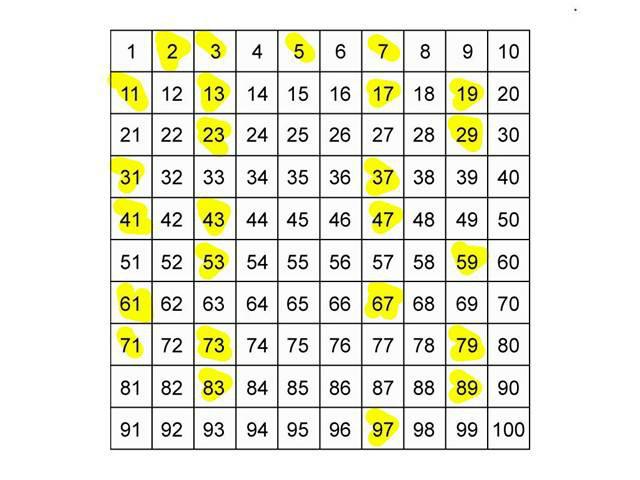
Греческий математик Эратосфен (275-194 гг. до н.э.) предложил интересный метод нахождения простых чисел в интервале [2; n]. Он написал на папирусе, натянутом на рамку, все числа от 2 до 10000 и прокалывал составные числа. Папирус стал, как решето, которое “просеивает” составные числа, а простые оставляет. Поэтому такой метод называется Эратосфеновым решетом. Рассмотрим подробнее этот метод.
Пусть написаны числа от 2 до n:
Первое неперечеркнутое число в строке является простым. Таким образом, 2 – простое число. Начинаем “просеивание” с него, перечеркивая все числа, которые делятся на 2:
Далее берем следующее по порядку неперечеркнутое число и перечеркиваем все числа, кратные ему и т. д. Таким образом, мы перечеркнем все составные числа, а простые останутся неперечеркнутыми:
Все числа указанного интервала можно рассматривать как множество и в дальнейшем из этого множества будем исключать (отсеивать) все составные числа.
Задача 6. Нахождение простых чисел с помощью решета Эратосфена.
Реализовать алгоритм решета Эратосфена с помощью организации работы с множествами.
Словесное описание алгоритма:
Цикл повторяется до тех пор, пока множество BeginSet не станет пустым. Программу нельзя использовать для произвольного n, т. к. в любом множестве не может быть больше 256 элементов. (Для расширения интервала простых чисел можно разбить одно большое множество на несколько маленьких, т. е. представить большое множество в виде массива малых множеств. Этот случай рассматривать не будем. Можно предложить наиболее заинтересованным учащимся самостоятельно рассмотреть этот вариант.)
Литература:
Определить, является ли число введенное пользователем, простым
Определить, является ли введённое число простым
Написать программу,которая определяет,является ли введённое число простым(делится на 1 или на само.
Определить, является ли простым натуральное число, введенное с клавиатуры
Определить, является ли простым натуральное число, введенное с клавиатуры. Простыми называются.

Здравствуйте! Помогите пожалуйста написать программу, которая проверяет, является ли целое число.

Решать с использованием файлов Написать программу, которая проверяет, является ли четным.
Добавлено через 1 минуту

Составить программу для решения следующей задачи: Дано натуральное число N. Является ли оно.

Помогите решить задание из задачника while 22. «Дано целое число N. Если оно является простым, то.

Написать программу, которая проверяет, является ли целое число, введенное пользователем, простым.
Определить, является ли заданное число простым
написать программу которая проверяет является ли целое число введенное с клав. простым ( то есть.
Как определить простое число
Программа находит простые числа (делятся только на 1 и на себя)…
Как определить простое число в Паскале
Алгоритм решения с подробным разбором приведу на Паскале. Решение на С++ можете посмотреть в примере программы на С++.
ВАЖНО!
На этом многие могут ошибиться. В определении сказано, что простое число имеет ровно два различных делителя. Следовательно, число 1 не является простым (также не является простым, так как ноль можно делить на любые числа).
Проверять, является ли число простым, будем с помощью функции, которую сами и создадим. Эта функция будет возвращать TRUE, если число простое.
В функции сначала будем проверять, не является ли число меньше двух. Если да, то это уже не простое число. Если же число равно 2 или 3, то оно является однозначно простым и делать какие-то дополнительные проверки не требуется.
А вот если число N будет больше трёх, то в этом случае в цикле будем перебирать все возможные делители, начиная от 2 до (N-1). Если на какой-то делитель число N делится без остатка, значит, это тоже не простое число. В этом случае мы прерываем цикл (потому что проверять дальше нет смысла), а функция возвращает FALSE.
Проверять, делится ли число на самоё себя нет смысла (поэтому цикл длится только до N-1).
Саму функцию здесь приводить не буду – посмотрите её в примерах программ.