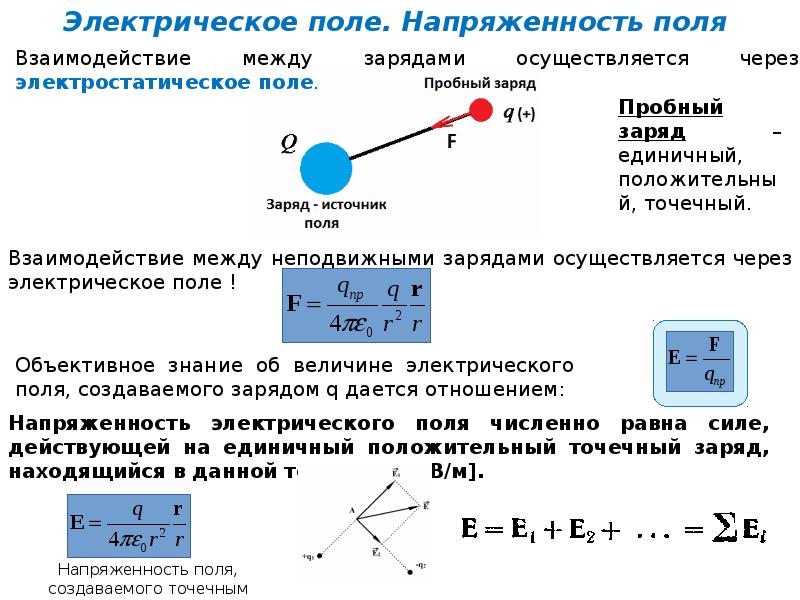
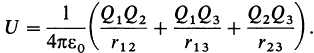как с помощью линий напряженности можно узнать где модуль вектора е больше или меньше

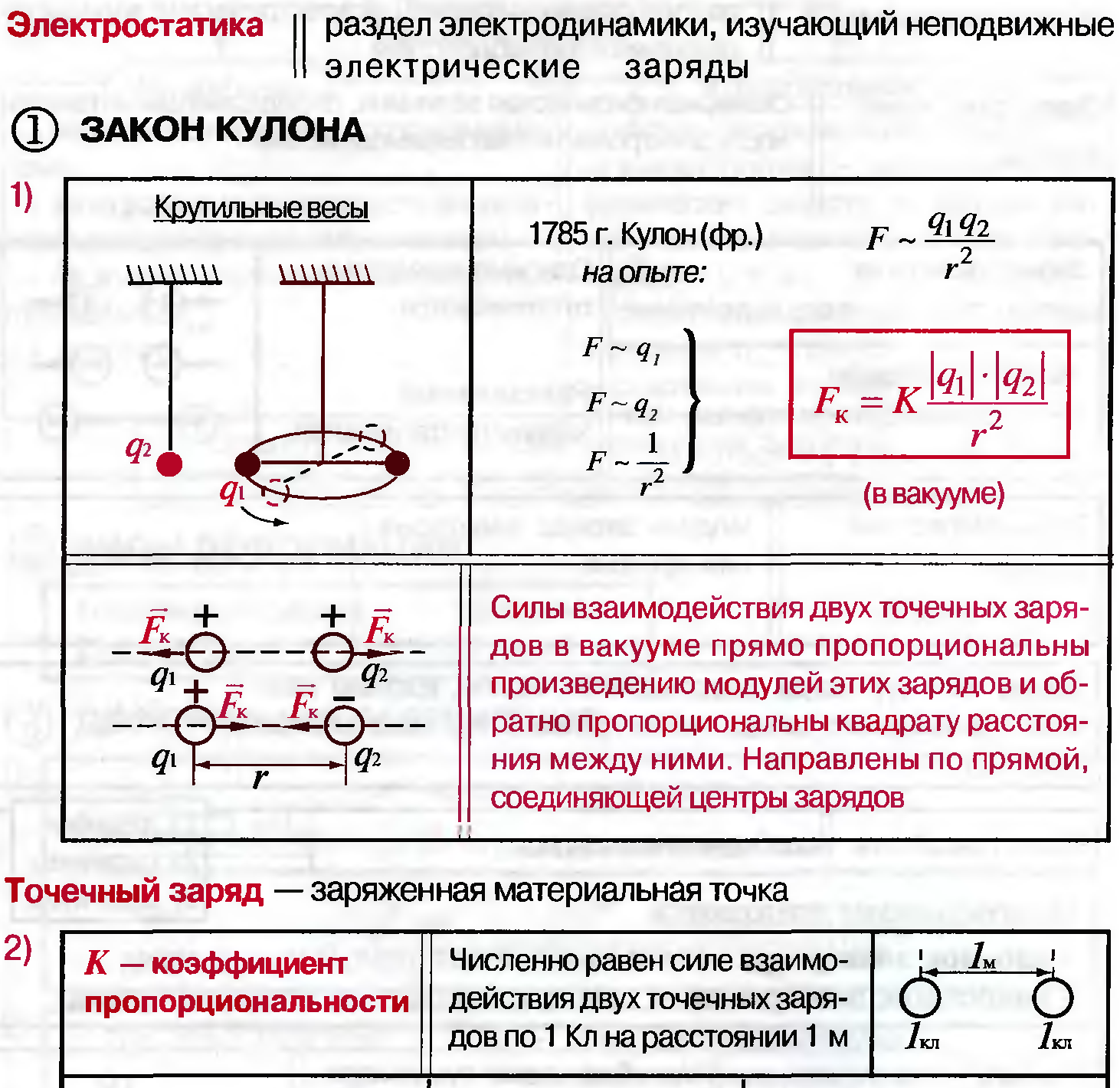
Силовые линии электрического поля — характеристика, свойства и направление

Направление силы, действующей на элементарный положительный заряд, обозначают силовыми линиями электрического поля. По сути, это воображаемые полоски со стрелками, позволяющими наглядно увидеть, как распространяется энергия при взаимодействии частиц.

Свойства и форма изображения распределения позволяет судить о течении явления, определять его главные характеристики. То есть анализировать поле, находить его неоднородности и величину напряжённости.

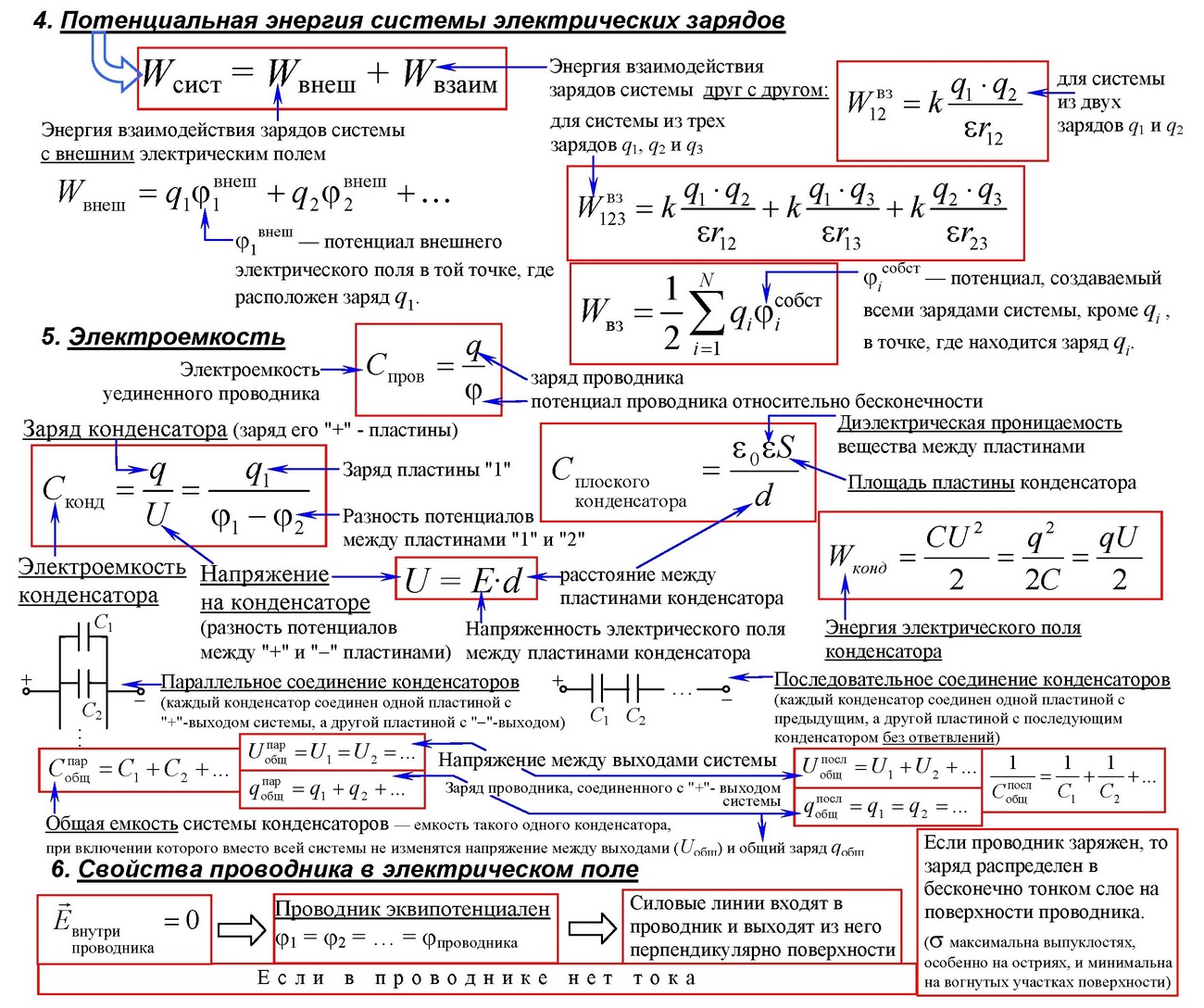
Общие сведения

Неким фундаментальным свойством природы является электрический заряд. Один из разделов физики занимается изучением его свойств и взаимодействия, называется он электродинамикой. Наиболее интересно для учёных изучение влияния друг на друга заряженных тел.

Бум исследования электрических явлений пришёлся на XIX век. В это время появилось две теории, одна из которых оказалась ошибочной и была опровергнута экспериментами. Эта догадка называлась правилом дальнодействия. Согласно ей один заряд непосредственно действует на другой. То есть чем больше расстояние между взаимодействующими телами, тем меньше сила действия.

Но на самом деле электрические заряды влияют друг на друга по-другому. Эта теория получила название «Правило близкодействия». Как оказалось, если взять два заряженных тела, например, положительно, то первый заряд на второй не действует. Он просто изменяет вокруг себя пространство, создавая нечто. Эта материя и получила название «Электрическое поле». Именно оно и воздействует на второе тело. Другими словами, на заряд действует материя, создаваемая первой частицей. При этом распространяется она с довольно большой, но конечной, скоростью.

Опыты, проводимые Фарадеем, показали, что если из системы убрать одно из тел, то сила, действующая на вторую частицу, не изменится мгновенно, хотя это и произойдёт довольно скоро. Именно Фарадей и является открывателем электромагнитного поля. В дальнейшем Максвелл смог описать явление теоретически.

Им было установлено, что заряд испытывает влияние поля, даже если поблизости его нет других частиц. Эта сила представляет собой электромагнитную волну.

Электрическое поле можно обнаружить, поместив в неё другой заряд, и исследовать действие наблюдающийся силы. Электромагнитную материю можно описать количественно, поэтому, зная характеристики поля и заряда, можно определить величину силы.

К основным параметрам электростатического поля, то есть материи, созданной неподвижной частицей в пространстве, относят:

Таким образом, если есть система заряженных тел, то в любой её точке будет существовать силовое электрическое поле. Его можно исследовать через силу, действующую на заряд, находящийся в этой материи.

Так как визуально вектор увидеть нельзя, то используют так называемые силовые линии, указывающие, куда направлено воздействие.

Свойство линий

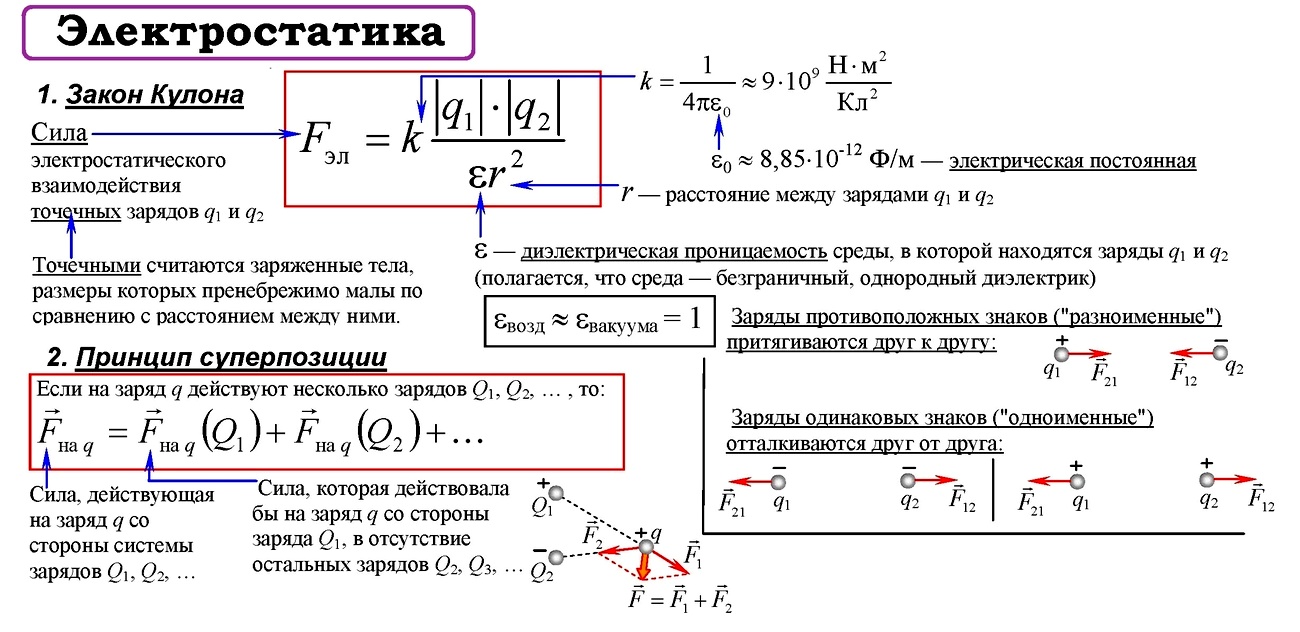
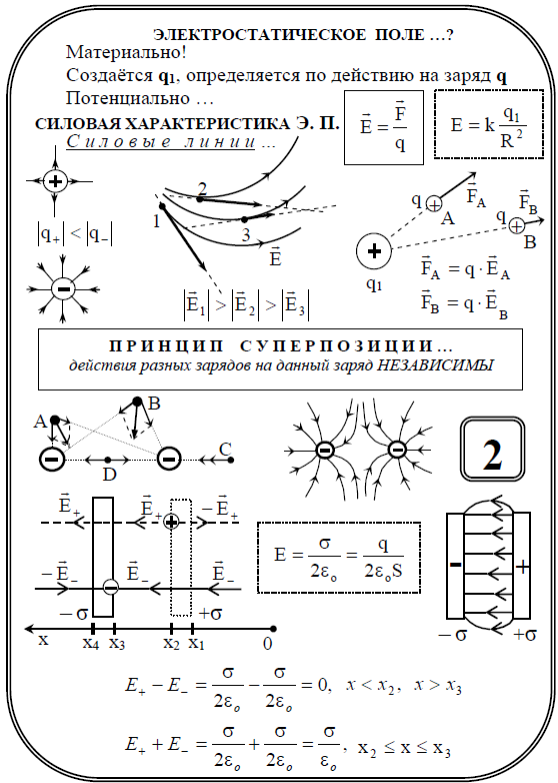
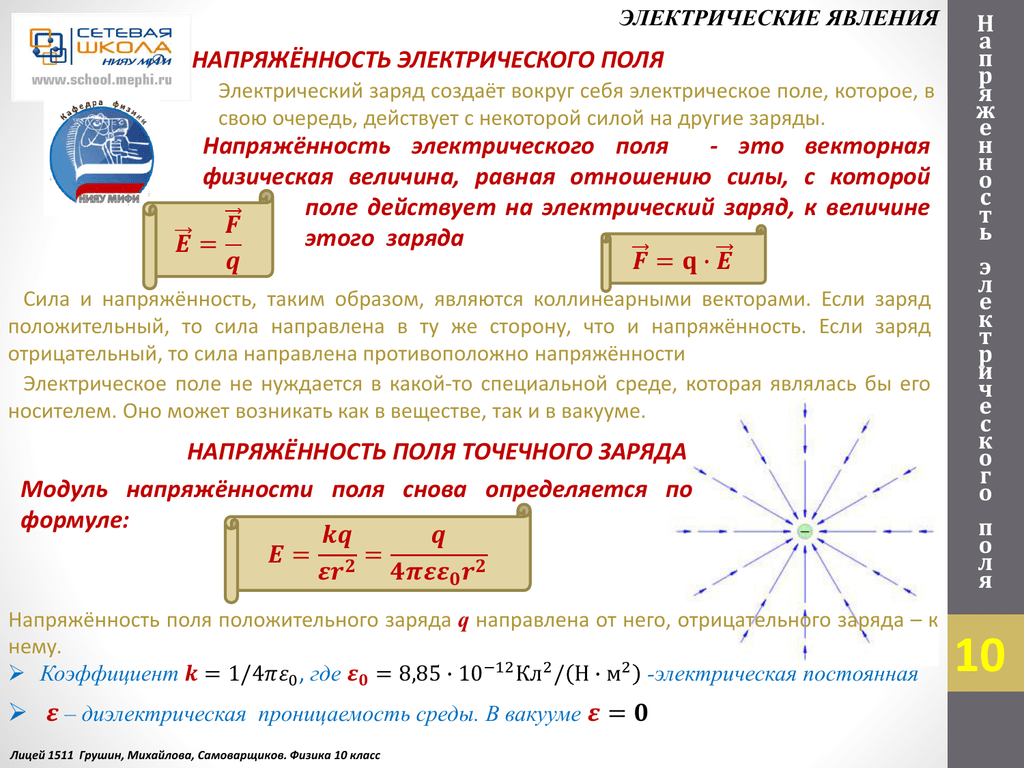
За величину силы электрополя в пространстве окутывающего тело принимают количество заряда обратного квадрату расстояния до него. Принято, что направление распространения действия направлено от положительного потенциала к отрицательному. Обозначают поле буквой E, а напряжённость H. Причём это векторная величина, представляемая в виде стрелки с определённой длиной и направлением.

Так как заряд — это источник, то его окружает множество векторов напряжённости. Чтобы не изображать их бесчисленное число, используют силовые линии. Другое их название — интегральные кривые. По сути, это объединённые векторы, где они сами являются касательными к точкам.

Распространение силовых кривых подчиняется определённым правилам.

К основным из них относят следующие:

Изображение линий подчиняется различными правилами. Так, для частиц с большим зарядом плотность линий должна быть выше, чем с меньшим. Если заряд недалеко от источника, то плотность силовых линий гуще. Для кривых проходящих перпендикулярно первичным силам используют эквипотенциальное изображение. Такой тип образуют замкнутые контуры. В них каждая точка напряжённости будет иметь одинаковое значение потенциала. При пересечении частицей линий говорят о совершении работы.

С помощью линий наглядно показывают направление вектора напряжённости в разных точках материи. Для этого их рисуют так, что касательная к каждой будет параллельна напряжённости. Но из-за того, что прямая указывает направление вектора с точностью до 180°, задают полярность обхода. Поэтому стрелку чертят так, чтобы она была сонаправлена с напряжённостью.

Силы электрического поля не могут пересекаться, а эквипотенциальные кривые образуют замкнутые контуры. В тех же точках, где линии перекрещиваются друг с другом, взаимодействие происходит в перпендикулярной плоскости.

Иными словами, на рисунке получается изображение, напоминающее собой координатную сетку. Причём по точкам пересечения и описывают характер электрополя.

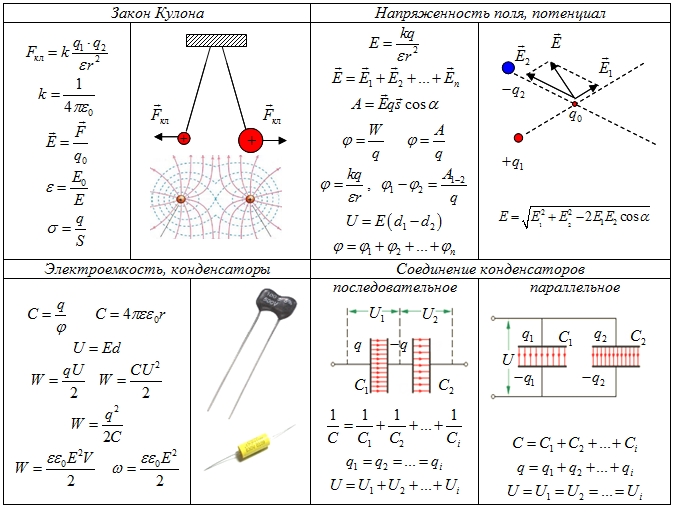
Напряжённость поля

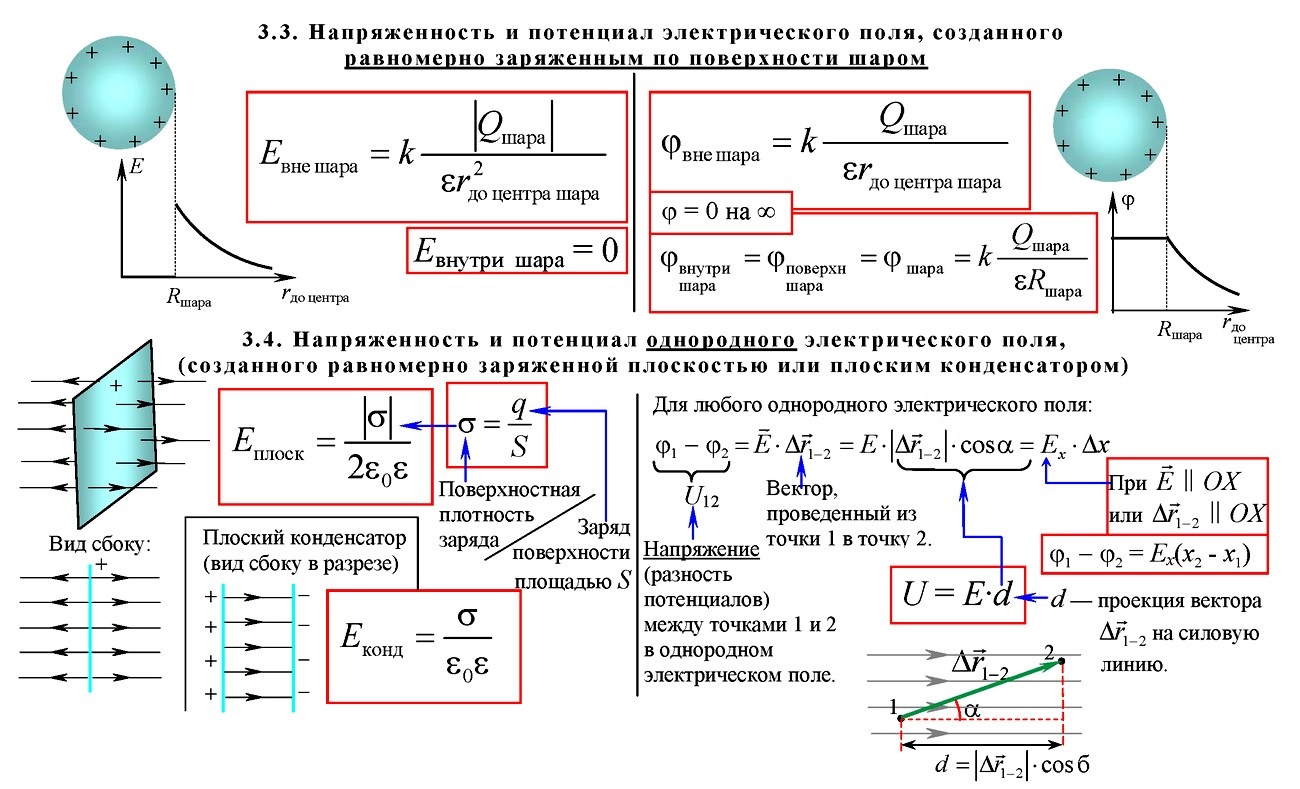
Взаимодействие между заряженными телами описывается количественной характеристикой, определяющей структуру материи. Эта величина называется напряжённостью и определяется из отношения E = F / q, где F — сила, а q — заряд, помещённый в поле. Для однородной изотропной среды выражение можно получить, используя закон Кулона: E = (1 / 4 pE) * (q * r / er 2 r), где r — радиус-вектор.

Линии распространения напряжённости поля одинокого заряда во всех точках имеют радиальный вид. Кривые лежат от частицы при q > 0, к телу при q Физика распространения

Если рассматривать одинокую частицу, то линии силы будут исходить от неё в радиальном направлении. При взаимодействии же двух и более зарядов на вид распространения влияет напряжённость. Чтобы нарисовать, как будут выглядеть линии, следует сложить векторы напряжённости. Их результирующая и будет характеризовать суммарное поле.

При составлении картинки распространения поля нужно учитывать, что точки соприкосновения на силовой линии определяются вектором напряжённости. Чтобы математически описать силовые кривые, необходимо составить уравнения. Вектора в них будут являться производными первого порядка. По сути, это обыкновенные касательные.

Каждая частица, добавленная в электромагнитное поле, оказывает на него влияние. Соответственно будет изменяться и узор кривых сил. Но в любом случае основой для построения визуализированного рисунка будет вектор напряжённости каждого источника поля. При этом правило, что линии напряжённости начинаются на положительном заряде, а заканчиваются на отрицательном, условное.

Довольно интересным для изучения является процесс возникновения электрического поля между заряженными бесконечными плоскостями. Созданная однородная материя между пластинками будет распространяться в параллельном направлении, то есть линии пересекаться не будут. Если же в зазор между ними внести точечный заряд, то кривые начнут изгибаться по дуге, поле станет неоднородным, а значение напряжённости будет зависеть от плотности.

Распространение поля подчиняется следующим правилам:

Электрические силы при внесении заряженной частицы в поле совершают работу. При незначительном воздействии её можно описать так: A = F * l * cos (a) = E * q * L. Таким образом, структура распространения зависит от расстояния между частицами.

Если же изменить направление перемещения заряженного тела на противоположное, то знак поменяет и работа. А это значит, что замкнутая траектория кулоновских сил будет равна нулю.

Источник

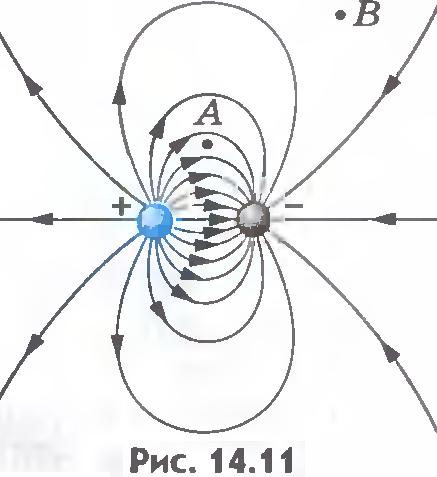
Линии напряжённости электростатического поля

Распределение электростатического поля в пространстве можно показать с помощью линий напряжённости вектора Е (силовых линий). Метод графического изображения электростатического поля с помощью линий напряжённости вектора Е разработал Фарадей.

Линией напряжённости вектора Е называется линия, проведённая в электростатическом поле так, что касательная к ней в каждой точке совпадает по направлению с вектором напряжённости Е электростатического поля. Линия напряжённости вектора Е направлена так, как и вектор Е в рассматриваемой точке линии (рис.79).

Линии напряжённости вектора Е электростатического поля, порождаемого электрическими зарядами, начинаются на

положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность. Они незамкнутые, всегда имеют начало и конец.

Линии напряжённости Е обладают следующим свойством. Вне заряженных тел они идут непрерывно, прерываясь лишь в точках, где имеются электрические заряды. Линии напряжённости вектора Е можно провести через любую точку исследуемого электростатического поля. Так как в каждой точке поля вектор Е имеет определенное направление, то линии напряжённости вектора Е нигде не пересекаются. Если бы они пересекались, то в точках пересечения напряжённость Е электростатического поля имела бы несколько значений.

Рис. 8 О

Плоские сечения электростатического поля, как положительного, так и отрицательного электрических зарядов, показаны на рис. 80.

Наглядное изображение электростатического поля с помощью линий вектора напряжённости Е позволяет определить направление вектора напряжённости Е и характер изменения величины Е в различных точках поля. Так, из рис. 79, 80 видно, что густота линий напряжённости вектора Е уменьшается по мере удаления от точечного электрического заряда (источника электростатического поля).

Поток Ф_Е вектора напряженности Е электростатического поля

Введем понятие потока Ф_Е вектора напряженности Е электростатического поля. Пусть произвольная плоская поверхность площадью S_±, расположена перпендикулярно линиям напряженности Е однородного электростатического поля.

перпендикулярно линиям напряженности Е поля.

В случае, если плоская поверхность S, имеющая прямоугольную форму со сторонами а ив, расположена в

пространстве произвольным образом, то ориентация площадки S определяется нормалью п (рис.82). Поведем плоскость,

Так как площадь S равна то

отсюда углы, отмеченные на рис. 82, равны, как углы с взаимно перпендикулярными сторонами

чтобы их можно было считать плоскими, а электростатическое поле однородным в пределах каждого участка.

Поток Дф. вектора напряженности Е через площадку д у равен

Если поверхность S замкнутая, то поток Ф_Е вектора напряжённости равен

Поток Ф_Е вектора напряженности может быть как положительным, так и отрицательным. Знак потока вектора Е зависит от выбора нормали к площадке. При замене направления нормали Я на противоположное направление, поток Ф_Е меняет знак.

Поток Ф_Е вектора напряженности положительный (Ф_; > 0), если направление линий напряженности вектора Е составляет острый угол с направлением нормали Я (cos а > 0), а если этот угол тупой (cos а 0,

Источник

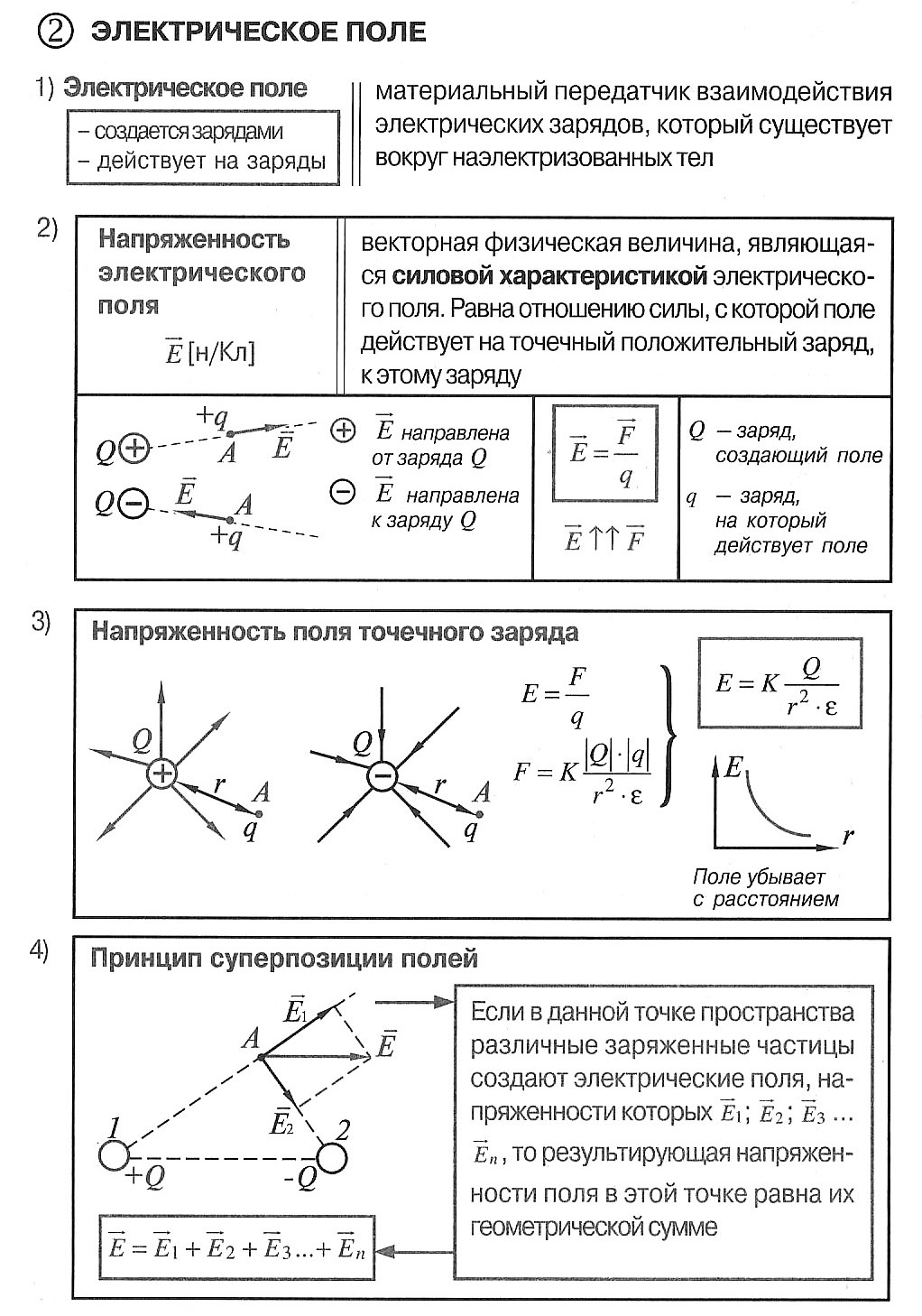
Вектор напряженности электрического поля

По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.

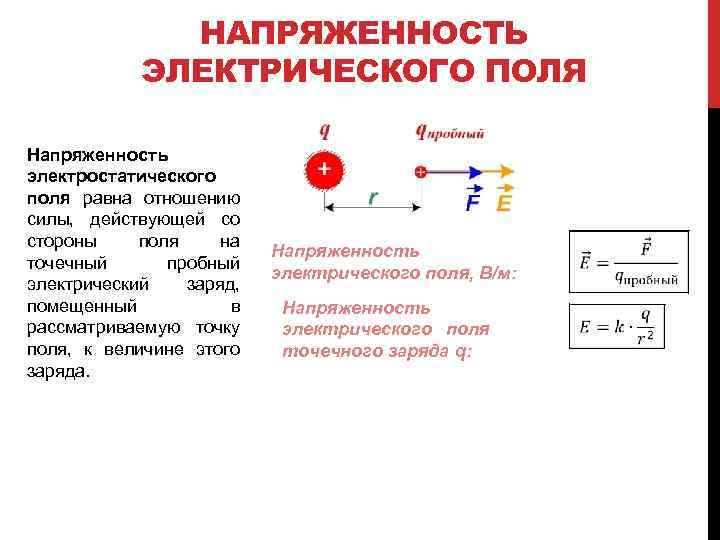
Характеристика электрического поля

Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:

У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.

Силовые линии

Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.

Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.

Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.

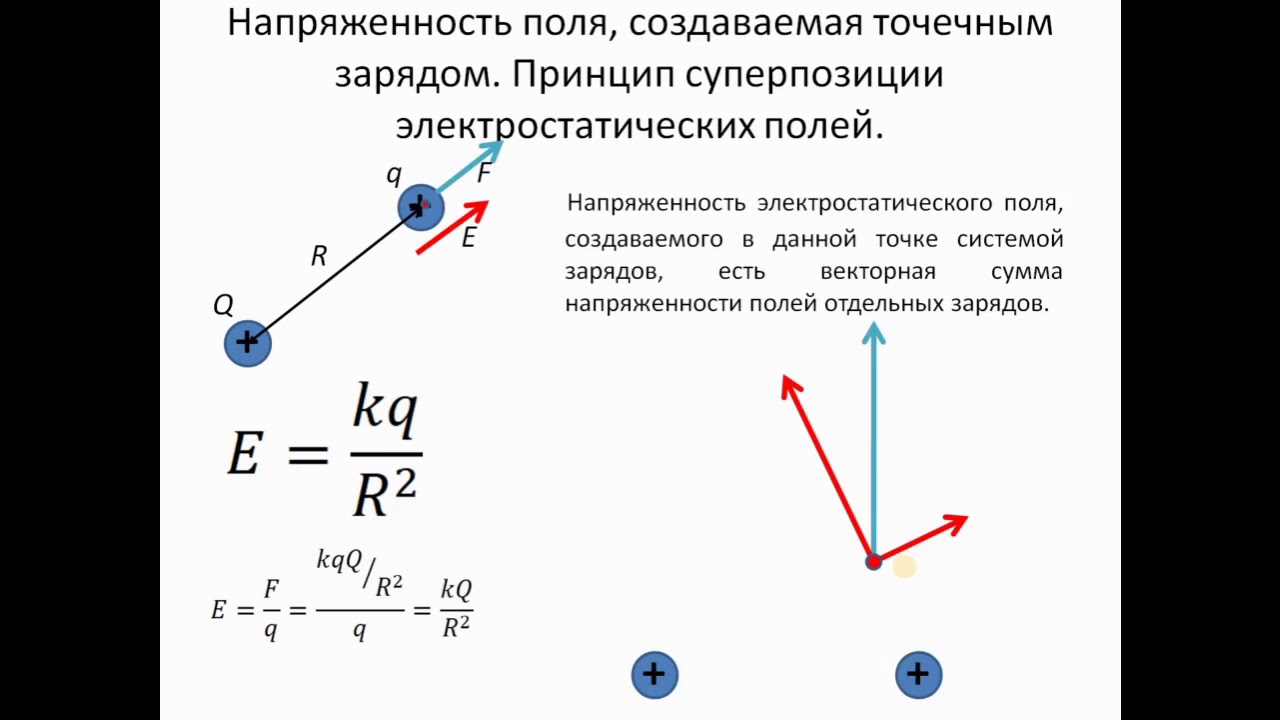
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:

Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:

Интегрирование по объему выполняется, если имеется объемное распределение заряда:

Что называется напряженностью электрического поля

Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:

Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:

Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.

Напряженность электростатического поля системы точечных зарядов равняется:

В системе СГС напряженность поля точечного заряда в вакууме:

Решение

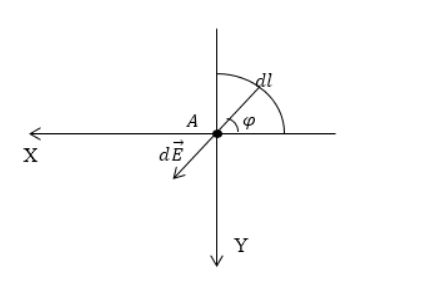
Проекция вектора d E → на ось О х составит:

Произведем выражение d q через линейную плотность заряда τ :

Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :

Перейдем к проекции вектора напряженности на О у :

Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :

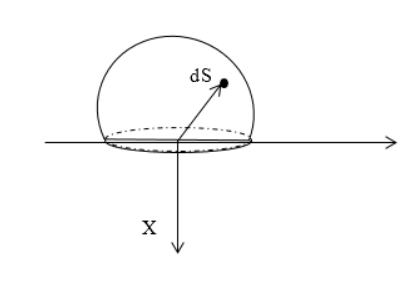
Решение

Элементарная напряженность поля точечного заряда в системе С И :

Необходимо спроецировать вектор напряженности на О х :

Произведем выражение заряда через поверхностную плотность заряда:

Источник

Определение напряженности в любой точке электрического поля

Разделы: Физика

Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.

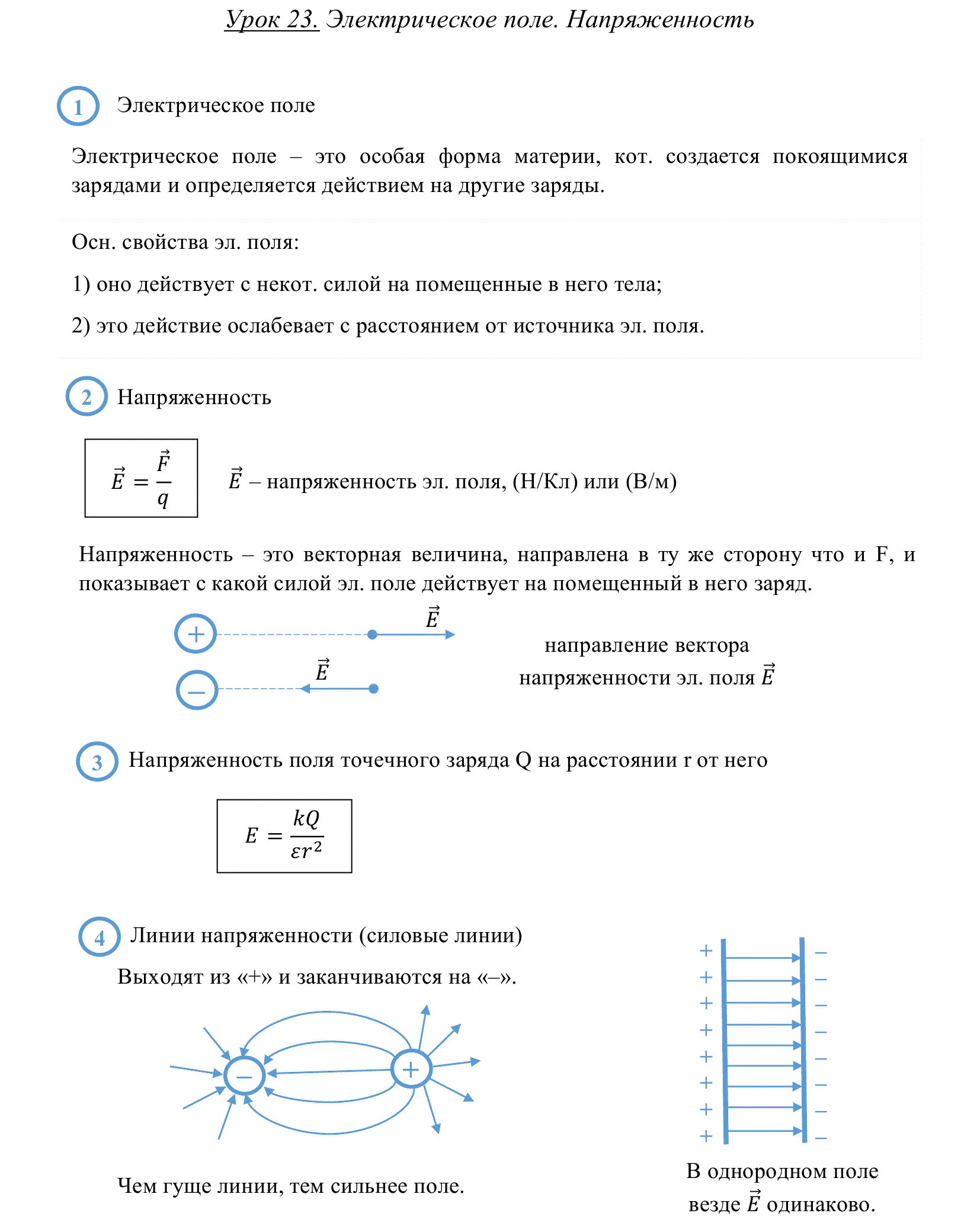
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности электрического поля:

Рис.1

Силовые линии положительного заряда:

Рис.2

Силовые линии отрицательного заряда:

Рис.3

Силовые линии одноименных взаимодействующих зарядов:

Рис.4

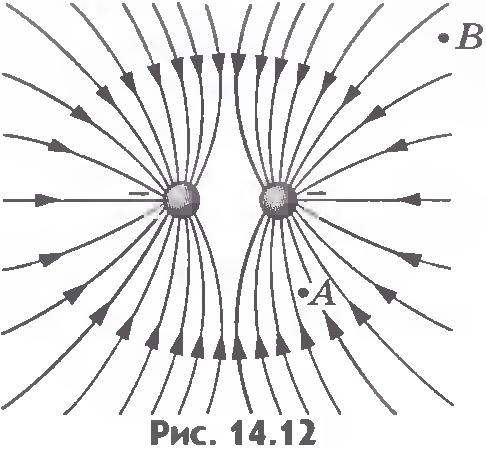
Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения или . Напряженность является векторной величиной, так как определяется отношением силы Кулона к величине единичного положительного заряда

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.

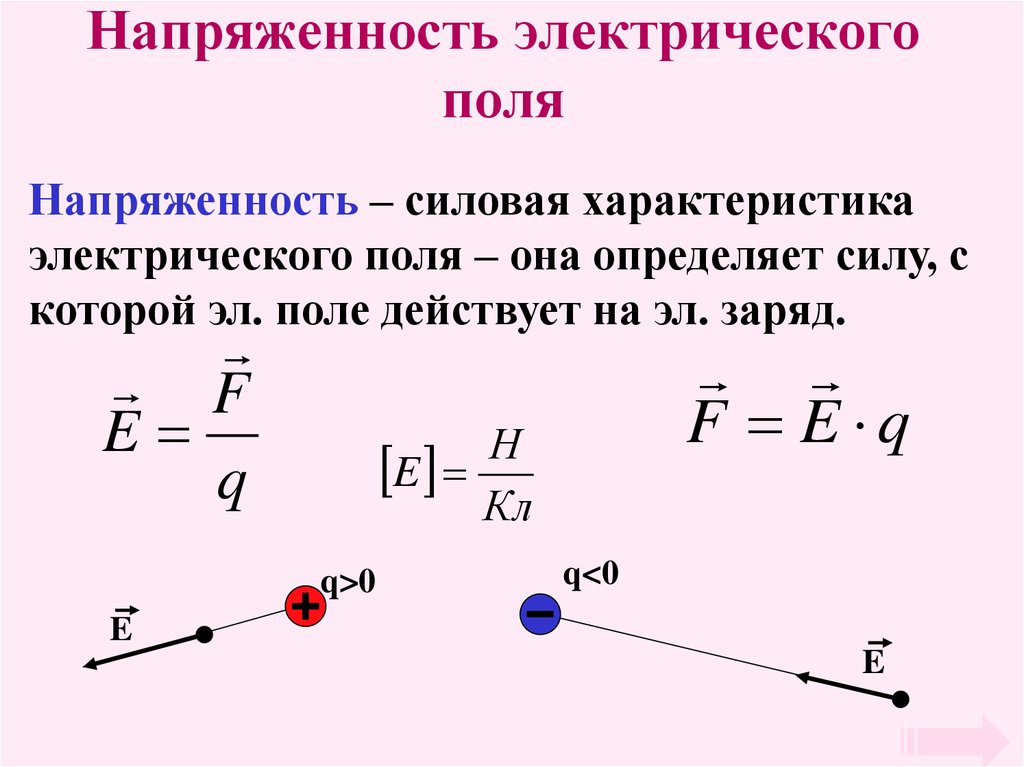
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

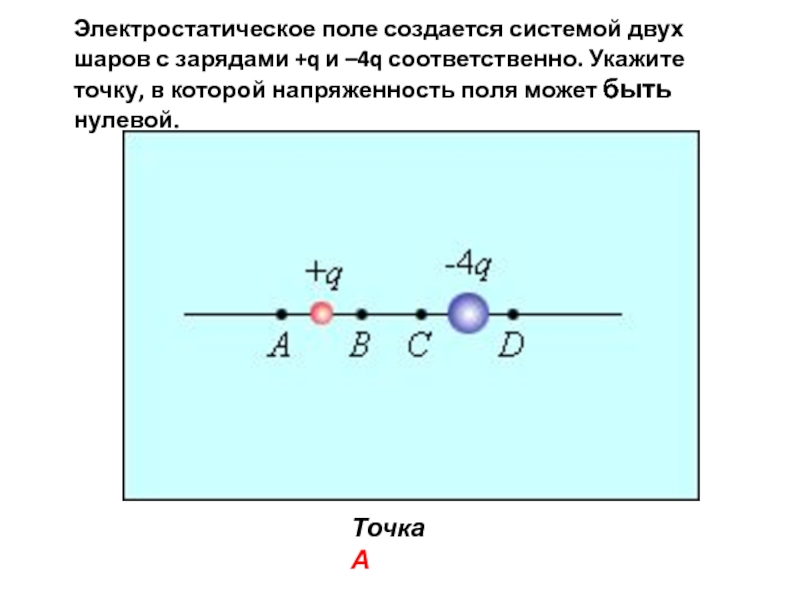
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a) 2 – kq₂/a 2

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Источник

Напряженность электрического поля

Закон обратных квадратов

Как и все формулы в физике, формулы для напряженности электрического поля могут быть использованы для алгебраического решения задач (проблем) физики. Точно также, как и любую другую формулу в ее алгебраической записи, можно исследовать и формулу напряженности электрического поля. Такое исследование способствует более глубокому пониманию сути физического явления и характеристик этого явления. Одна из особенностей формулы напряженности поля является то, что она иллюстрирует обратную квадратичную зависимость между напряженностью электрического поля и расстоянием до точки в пространстве от источника поля. Сила электрического поля, создаваемого в источнике заряде Q обратно пропорционально квадрату расстояния от источника. Иначе говорят, что искомая величина обратно пропорциональна квадрату.

Напряженность электрического поля зависит от геометрического места в пространстве, и ее величина уменьшается с увеличением расстояния. Так, например, если расстояние увеличится в 2 раза, то напряженность уменьшится в 4 раза (22), если расстояния между уменьшится в 2 раза, то напряженность электрического поля увеличится в 4 раза (22). Если же расстояние увеличивается в 3 раза, то напряженность электрического поля уменьшается в 9 раз (32). Если расстояние увеличивается в 4 раза, то напряженность электрического поля уменьшается в 16 (42).

Направление вектора напряженности электрического поля

Как упоминалось ранее, напряженность электрического поля является векторной величиной. В отличие от скалярной величиной, векторная величина является не полностью описанной, если не определено ее направление. Величина вектора электрического поля рассчитывается как величина силы на любой пробный заряд, расположенный в электрическом поле.

Сила, действующая на пробный заряд может быть направлена либо к источнику заряда или непосредственно от него. Точное направление силы зависит от знаков пробного заряд и источника заряда, имеют ли они тот же знак заряда (тогда происходит отталкивание) или же их знаки противоположные (происходит притяжение). Чтобы решить проблему направления вектора электрического поля, направлен он к источнику или от источника были приняты правила, которые используются всеми учеными мира. Согласно этим правилам направление вектора всегда от заряда с положительным знаком полярности. Это можно представить в виде силовых линий, которые выходят из зарядов положительных знаков и заходят в заряды отрицательных знаков.

«Материальные уравнения»

Для решения многих практических задач вполне достаточна ограниченная точность. С помощью «материальных» уравнений выполняют расчеты различных электрических цепей.

Уместный пример – закон Ома. Он был создан в ходе измерения электрических параметров. В начальном виде формула (Х=П/L+B) состояла из следующих компонентов:

Несложно догадаться, что в современном представлении это известный закон, показывающий взаимное влияние основных параметров полной электрической цепи:

Более подробно о формуле напряженности электрического поля

Выше мы коснулись определения напряженности электрического поля в том, как она измеряется. Теперь мы попробуем исследовать более развернутое уравнение с переменными, чтобы яснее представить саму суть вычисления и измерения напряженности электрического поля. Из уравнения мы сможем увидеть, что именно влияет, а что нет. Для этого нам прежде всего потребуется вернутся к уравнению Закона Кулона.

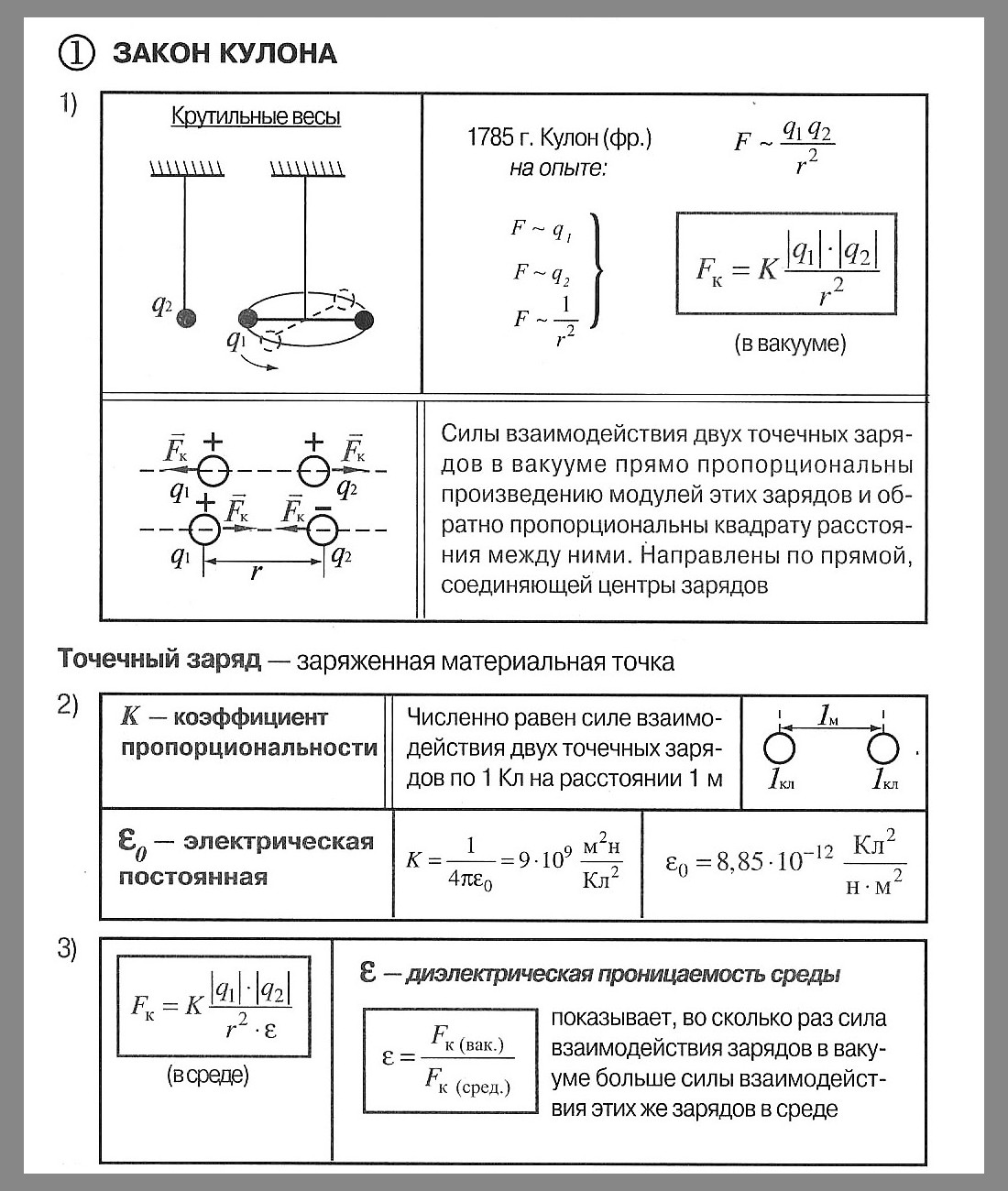
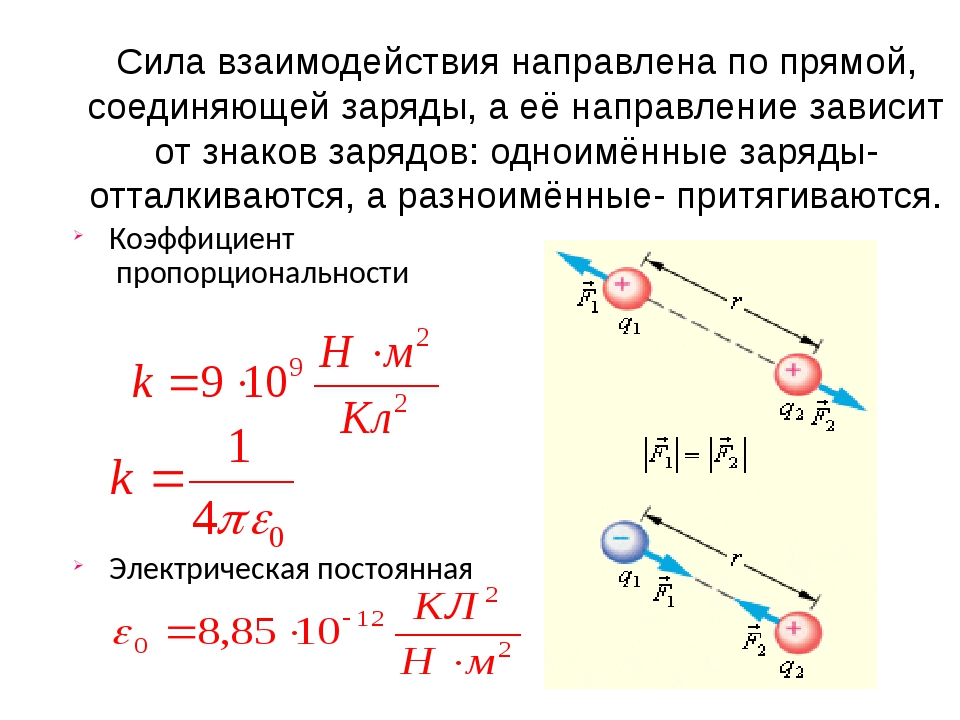
Закон Кулона утверждает, что электрическая сила F между двумя зарядами прямо пропорциональна произведению количества этих зарядов и обратно пропорциональна квадрату расстояния между их центрами.

Если внести в уравнение Закона Кулона два наших заряда Q (источник) и q (пробный заряд), тогда мы получим следующую запись:

Если выражение для электрической силы F, как она определяется Законом Кулона подставить в уравнение для напряженности электрического поля E, которое приведено выше, тогда мы получим следующее уравнение:

Обратите внимание, что пробный заряд q был сокращен, то есть убран как в числителе так и в знаменателе. Новая формула для напряженности электрического поля E выражает напряженность поля в терминах двух переменных, которые влияют на нее

Напряженность электрического поля зависит от количества исходного заряда Q и от расстоянии от этого заряда d до точки пространства, то есть геометрического места, в котором и определяется значение напряженности. Таким образом у нас появилась возможность характеризовать электрическое поле через его напряженность.

Напряжённость электрического поля в классической электродинамике

Для лучшего понимания темы необходимо напомнить несколько базовых определений. Существуют отрицательные и положительные электрические заряды. Каждый из них не зависит от системы координат, что подразумевает отсутствие влияния скорости. В изолированном объеме сумма зарядов не изменяется. Базовой величиной считают Кулон, который соответствует прохождению тока через единичную площадь сечения проводника за одну секунду.

Описывает напряженность электрического поля формула с векторными составляющими:

Вместе с вектором магнитной индукции напряженность (Е) формирует электромагнитное поле. Суммарное воздействие сил образует тензор. Вместе с зарядом это главные параметры электродинамики.

Как направлен вектор электрического поля

Вектор поля надо направить в сторону от положительного заряда и в обратном направлении – к отрицательному. Это определение справедливо для одной точки. Так как идеальные условия отсутствуют, в реальной ситуации приходится учитывать взаимодействие зарядов и соответствующее образование силовых линий.

Силовые линии

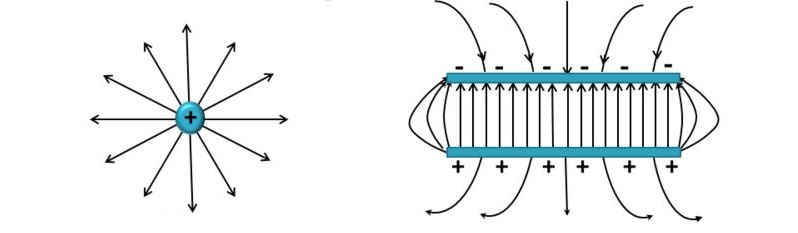
Поле не является однородным, что демонстрируют с помощью разных расстояний между отдельными линиями. В примере с пластинами близкое расположение параллельных проводников позволяет обеспечить одинаковую напряженность в рабочей зоне. Все силовые линии бесконечные. Они начинаются на положительном заряде и заканчиваются на отрицательном. Таким образом, направление вектора напряженности будет всегда в сторону уменьшения потенциала.

Электростатика

Занимается частными случаями, когда заряженные тела являются неподвижными, или их скорость передвижения настолько мала, что их таковыми считают. Как же посчитать напряженность электрического поля в данном случае? В этом нам поможет скалярный потенциал:

НЭП – напряженность электрического поля.

СП – скалярный потенциал.

Верно и обратное. Полученное значение называется электростатическим потенциалом. Также подобный подход упрощает уравнение Максвелла, и оно превращается в формуле Пуассона. Для частного случая областей, которые свободны от заряженных частиц, используют подсчёты по методу Лапласа

Обратите внимание – все уравнения линейные, а соответственно, к ним применяется принцип суперпозиции. Для этого следует найти поле только одного точечного единичного заряда

Затем следует обсчитать напряженность или потенциал поля, что создаются их распределением. Знаете, как называют полученный результат? Наверняка нет. А имя ему — напряженность электрического поля точечного заряда.

Воздействие поля на заряды

При воздействии полей предполагается, что в полную силу входят магнитные и электрические составляющие. Она выражается в так называемой формуле по силе Лоренца:

Своим значением наделён каждый элемент в этом определении напряжённости электрического поля, формула без них не будет точной:

Косой крест применяют для обозначения векторного произведения. Единицы измерения для формулы – СИ. Заряды тоже становятся частью общей системы.

Новые значения – более общие по сравнению с формулой, чьё описание приведено ранее. Причина – в том, что частица под воздействием сил.

Обратите внимание. Предполагается, что частица в этом случае – точечная

Но благодаря этой формуле просто определить воздействие на тела вне зависимости от текущей формы. При этом распределение зарядов и токов внутри не имеет значения. Главное – уметь рассчитывать E и B, чтобы применять формулу правильно. Тогда проще проводить и определение напряжённости поля, формулы с другими цифрами.

Измерение

Напряжённость относят к векторным величинам, оказывающим силовое воздействие на заряженные частицы.

Существуют не только теоретические, но и практические способы для измерения напряжённости.

Если речь о произвольных – сначала берут тело, содержащее заряд. Это правило распространяется на любые электронные устройства.

Размеры тела должны быть меньше размеров другого тела, генерирующего заряд. Достаточно небольшого металлического шарика, у которого есть свой заряд. Заряд шарика измеряют электрометром, потом приспособление помещают внутрь. Динамометр уравновешивает силу, воздействующую на предмет. После этого можно снять показания с единицей измерения – Ньютонами.

В бытовых условиях

Значение напряжённости получают, разделив значение силы на величину заряда.

Измерить расстояние – первый шаг, когда определяют напряжённость в конкретной точке, удалённой от тела на какую-либо величину.

Полученную величину разделяют на расстояние, возведённое в квадрат. К полученному результату применяют специальный коэффициент. Его выражение такое: 9*10^9.

Отдельного изучения заслуживает ситуация с конденсаторами.

В данном случае первый этап – измерение напряжения между пластинами. Предполагается использование вольтметра. Потом определяются с расстоянием между этими пластинами. Единица измерения – метры. Получают результат, который и будет напряжённостью. Направлять её можно по-разному.

Электростатика

Этот раздел электродинамики описывает частный случай, когда заряженные тела находятся в статичном состоянии. Такая ситуация значительно упрощает расчеты. Для практического примера можно создать электростатический конденсатор.

Устанавливают две плоскости одинаковой размерности параллельно на небольшом расстоянии, разделяют слоем диэлектрика. Если создать разницу потенциалов, между поверхностями образуется поле. В такой конструкции накапливается электрический заряд. Какой будет емкость, можно узнать с помощью этой формулы:

Конденсатор

Чтобы зарядить конденсатор до нужной емкости, надо затратить энергию W=(e*e0*E2/2)*S*D. На рисунке показано, как изменять рабочие параметры сборки при последовательном и параллельном соединении модулей.

Теорема Гаусса

Эта теорема определяет пропорциональность потока вектора напряженности электрического поля (Ф) заряду (Q), который заключен в произвольную поверхность замкнутого типа:

Напряжённость электрического поля точечного заряда

В этом случае можно пользоваться рассмотренным выше законом Кулона. В следующих разделах представлены формулы для вычисления в разных системах единиц.

В единицах СИ

В этой системе базовой выбрана сила тока, поэтому кулон является производной величиной.

Здесь коэффициент k=1/(4π*e0).

Для системы СГС

Здесь, как и в предыдущем примере, выбран единичный заряд – «точка». Основные правила характеризуют физические процессы аналогично. Разница лишь в постоянных величинах. В данном случае коэффициент k обратно пропорционален диэлектрической проницаемости (е) среды.

В этом варианте для получения результата надо сложить вектора каждого заряда:

Чтобы обеспечить непрерывность линии напряженности, берут интеграл соответствующей области. Построить распределение силовых линий можно с помощью расчета перемещения вектора по всем точкам.

Сила действия на заряженные частицы

Для выражения общего показателя воздействия магнитного поля использую формулу Лоренца:

С – сила воздействия магнитного поля на заряженную частицу.

ЭЗЧ – электрический заряд одной частицы.

ВМИ – вектор магнитной индукции.

Ск – скорость движения частицы.

Если разобраться в формуле, то можно увидеть, что она полностью согласуется с ранее данным определением, чем является напряженность электрического поля. Но само уравнение обобщено, поскольку в него включено действие на заряженную частицу со стороны магнитного поля при движении оной. Также предполагается, что объект рассмотрения является точечным. Формула позволяет рассчитывать силы, которыми действует электромагнитное поле на тело любой формы, в котором произвольное распределение зарядов и токов. Необходимо только разбить сложный объект на маленькие части, каждая из них может считаться точкой, и тогда к ней становится возможным применение формулы.

Формула силы электрического поля

В большинстве случаев учёные применяют стандартную формулу:

Своё значение вектора, который обозначается как E, существует в каждой отдельной временной точке. В форме записи этот показатель тоже имеет свою фиксацию:

Интересно. Таким образом, это функция пространственных координат. Допустимо изменение характеристики по мере течения времени. За счёт этого происходит образование электромагнитного поля, учитывающего и вектор магнитной индукции. Его регулируют законы термодинамики, то же касается напряжённости электрического поля, формула через заряды тоже давно известна.

Замеры напряжённости

Электростатическая потенциальная энергия

Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы
в которых, обусловленные другими зарядами, равны соответственно V_a и V_b. Изменение электростатической
потенциальной энергии заряда q в поле других зарядов составляет:

Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы?
Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга.
Потенциальная энергия уединенного точечного заряда Q₁ равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила. Если к нему поднести второй точечный заряд, Q₂, потенциал в точке, где находится второй заряд, будет равен:

Здесь r_{1 2} — расстояние между зарядами. Потенциальная энергия двух зарядов равна:

Она характеризует работу, необходимую для перемещения заряда Q₂ из бесконечности (V = 0) на расстояние r_{1 2} до
заряда Q_i (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).

Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения. Работа по сближению зарядов Q₂ и Q₁ определяется выражением (24.10);
чтобы перенести заряд Q₃ из бесконечности в точку на расстоянии r_{1 3} от Q₁ и на расстоянии r_{2 3} от Q₂, требуется совершить работу:

В этом случае потенциальная энергия системы трех точечных зарядов будет равна:

Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды).
Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее. Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q₁ и -Q₁ первого диполя и Q₂ и -Q₂ второго диполя.
Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния. В этом случае нас не интересует взаимная потенциальная энергия зарядов Q₁ и -Q₁ или Q₂ и -Q₂; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q₁ и Q₂ ; Q₁ и -Q₂ ; -Q₁ и Q₂ ; -Q₁ и -Q₂.

Примечания

Определение

Напряженность относят к величинам физического характера. Как уже говорилось, это силовой параметр. Равен обычно соотношению между силой, действующей на заряженное тело, и значением.

Измерение напряжённости

Важно. Показатель напряжённости относят и к векторным величинам

Определяют, с каким значением действует сила на заряженные предметы. При необходимости упрощает определение направления. Главная единица измерения – ньютон на кулон.

Определение напряжённости упрощает организацию измерения показателя. Если заранее знать значение энергии того или иного тела – проще измерить характеристику, воздействующую на него. Как найти напряжённость – объяснено дальше.

Сила порождаемая электрическими зарядами

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.

Силовые линии электрического поля.

Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.

Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой и каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.

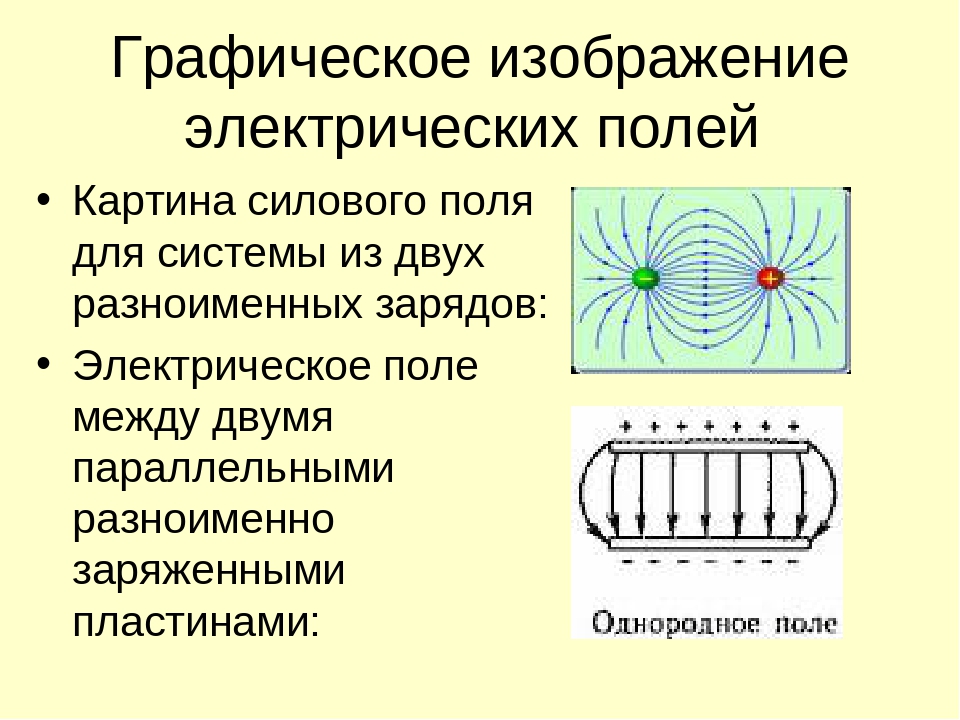
На рисунках ниже изображены линии напряженности положительно заряженного шарика (рис. 1); двух разноименно заряженных шариков (рис. 2); двух одноименно заряженных ша­риков (рис. 3) и двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами (рис. 4).

Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства одно­родно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.

В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересе­чение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.

Постоянный электрический ток

Электрический ток – направленное движение свободных носителей энергии в веществе или внутри вакуума. Этот показатель появляется при соблюдении главных условий:

I – буква, которую применяют для обозначения силы тока.

Пример задачи с напряжённостью

Важно. Единица измерения – Амперы

Величина тока зависит от количества электричества или разрядов, которые проходят через поперечное сечение у проводника в единицу времени.

Когда речь о постоянном токе – предполагается, что с течением времени не меняются его направление, основная величина.

Вектор

Амперметр – устройство, применяемое для измерения силы тока. Его подключение к цепи – последовательное. Показатель важен, поскольку от него зависят и сила воздействия и другие подобные параметры. На практике часто встречаются ситуации, когда сила тока заменяется плотностью. В данном случае единица измерения – Ампер на метр квадратный. Площадь сечения проводов выражается в мм2. И плотность тока предполагает опору на эту характеристику.

Электрическое поле можно назвать реально существующим явлением, как и любые предметы. Поле и вещества относят к основным формам существования материи. Способность действовать с силой на заряды – главное свойство. Его используют, чтобы обнаруживать, измерять явления. Ещё одна характеристика – распространение со скоростью света

Это тоже важно для тех, кто занимается изучением подобных факторов

Примечания

Заключение

Что же, подводя итог, можно сказать, что напряженность электрического поля была рассмотрена довольно полно, как в целом, так и некоторые частные случаи. Данных, представленных в рамках статьи, должно с лихвой хватить, чтобы рассчитывать параметры для своих будущих конструкций. Про графическое изображение можно сказать, что векторы напряженности электрического поля изображаются с помощью силовых линий, которые считаются касательными к каждой точке. Этот способ описания впервые был введён Фарадеем

На этом про напряженность электрического поля автор заканчивает и благодарит вас за уделенное внимание

Заключение

Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:

Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.

где r — расстояние от элемента заряда dq до точки, в которой определяется V.

Продолжение следует. Коротко о следующей публикации:Электрическая емкость, диэлектрики, накопление электрической энергии.Конденсатор — устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.

Альтернативные статьи: Постоянный ток, Переменный ток.

Замечания и предложения принимаются и приветствуются!

Источник