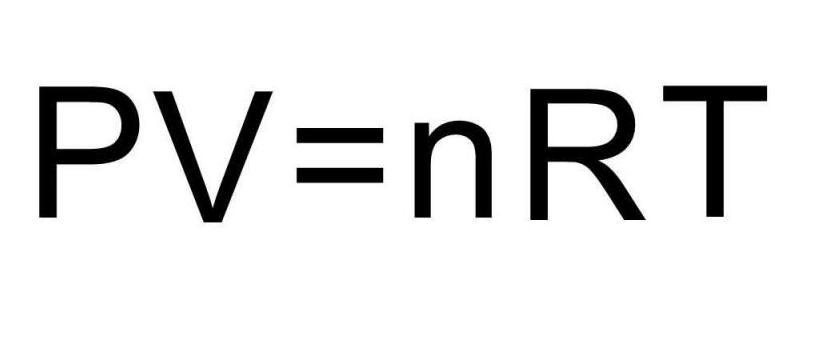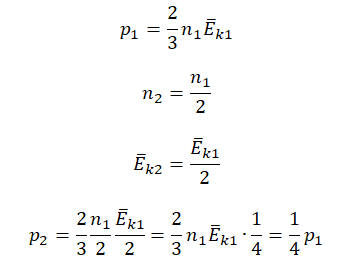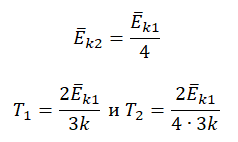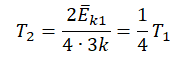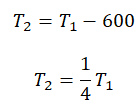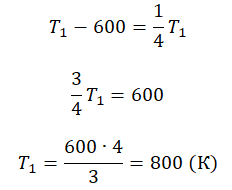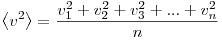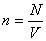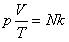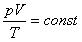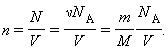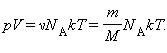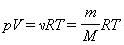как узнать абсолютную температуру газа

Абсолютная температура идеального газа. Формулы. Пример задачи

Абсолютная шкала температур

Для начала познакомимся со шкалой, которая используется в физике для описания температуры. Она называется абсолютной или шкалой Кельвина. Впервые ее ввел в использование английский физик лорд Кельвин в 1848 году. При этом ученый основывался на завоевавшей популярность шкале Цельсия.

С градусами Цельсия C абсолютная шкала T связана следующим простым равенством:

В отличие от других температурных шкал, например, от шкалы Фаренгейта, кельвин имеет точно такой же масштаб, что и градус Цельсия. Последнее означает, что для перевода в абсолютную любой температуры по Цельсию достаточно добавить к ней число 273,15. Так, по шкале Кельвина вода замерзает при 273,15 К, а кипит при 373,15 К.

Краткое понятие о газе идеальном

Поскольку далее будет рассмотрена формула для определения абсолютной температуры газа идеального, то будет полезным познакомиться с этим понятием поближе. Под идеальным понимают такой газ, молекулы которого практически не взаимодействуют друг с другом, обладают большой кинетической энергией по сравнению с потенциальной, и расстояния между которыми значительно превышают их собственные размеры.

Температура абсолютная идеального газа

Существует два подхода к определению температуры в газах. Рассмотрим каждый из них.

Первый подход заключается в привлечении положений молекулярно-кинетической теории (МКТ) и физического смысла самой температуры T. Последний заключается в кинетической энергии частиц газа. Чем больше эта энергия, тем выше температура, причем зависимость является прямо пропорциональной. Используя формулу из механики для энергии кинетической и постоянную Больцмана k_B можно записать следующее равенство МКТ:

Чем меньше масса частицы и чем больше ее скорость, тем выше абсолютная температура.

Второй подход в определении величины T заключается в использовании универсального уравнения Клапейрона-Менделеева. Это уравнение было записано в XIX веке Эмилем Клапейроном (впоследствии модифицировано Д. И. Менделеевым) как результат обобщения открытых экспериментально в XVII-XIX веках газовых законов (Шарля, Гей-Люссака, Бойля-Мариотта, Авогадро). Математически универсальное уравнение записывается так:

Не представляет особого труда получить формулу для температуры из Клапейрона-Менделеева закона:

В закрытой системе (n = const) температура газа прямо пропорциональна произведению объема на давление.

Пример задачи

Воздух, которым мы дышим, является смесью газов идеальных. Известно, что молярная масса воздуха составляет 29 г/моль. Необходимо определить температуру воздуха, если средняя скорость его молекул составляет 530 м/с.

Очевидно, что решение этой задачи можно получить, если воспользоваться следующим выражением:

T = M*v 2 /(3*R ) = 0,029*600 2 /(3*8,314) = 326,60 К.

В градусах Цельсия найденной температуре соответствует значение 53,45 o C. На нашей планете такие температуры характерны для жарких песчаных пустынь в полдень.

Источник

Уравнение состояния идеального газа и смысл абсолютной температуры

Каждый человек в течение своей жизни сталкивается с телами, которые находятся в одном из трех агрегатных состояний вещества. Самым простым для изучения агрегатным состоянием является газ. В статье рассмотрим концепцию идеального газа, приведем уравнение состояния системы, а также уделим некоторое внимание описанию абсолютной температуры.

Газовое состояние вещества

Каждый школьник хорошо представляет, о каком состоянии материи идет речь, когда слышит слово «газ». Под этим словом понимают тело, которое способно занимать любой предоставленный ему объем. Оно не способно сохранять форму, поскольку не может сопротивляться даже самому незначительному внешнему воздействию. Также газ не сохраняет и объем, что его отличает не только от твердых тел, но и от жидкостей.

Вам будет интересно: Как правильно писать? Выберете или выберите?

Как и жидкость, газ является текучей субстанцией. В процессе движения твердых тел в газах последние препятствуют этому движению. Появившуюся силу называют сопротивлением. Ее величина зависит от скорости движения тела в газе.

Яркими примерами газов является воздух, природный газ, который используется для отопления домов и приготовления пищи, инертные газы (Ne, Ar), которыми заполняют рекламные трубки тлеющего разряда, или которые используют для создания инертной (неагрессивной, защитной) среды при сварке.

Идеальный газ

Вам будет интересно: Людовик Сварливый: его краткое правление, жены и сын, Иоанн Посмертный

Прежде чем переходить к описанию газовых законов и уравнения состояния, следует хорошо разобраться с вопросом, что собой представляет идеальный газ. Это понятие вводится в молекулярно-кинетической теории (МКТ). Идеальным называется любой газ, который удовлетворяет следующим характеристикам:

Естественно, что любой газ является не идеальным, а реальным. Тем не менее, для решения многих практических задач указанные приближения являются вполне справедливыми и ими можно пользоваться. Существует общее эмпирическое правило, которое гласит: независимо от химической природы, если газ имеет температуру выше комнатной и давление порядка атмосферного или ниже, то его с высокой точностью можно считать идеальным и применять для его описания формулу уравнения состояния идеального газа.

Закон Клапейрона-Менделеева

Вам будет интересно: Идеальный газ. Уравнение Клапейрона-Менделеева. Формулы и пример задачи

Переходами между различными агрегатными состояниями вещества и процессами в рамках одного агрегатного состояния занимается термодинамика. Давление, температура и объем являются тремя величинами, которые однозначно определяют любое состояние термодинамической системы. Формула уравнения состояния идеального газа объединяет в единое равенство все три указанные величины. Запишем эту формулу:

Другие формы записи уравнения

Выше мы записали уравнение состояния идеального газа Менделеева-Клапейрона в общепринятом и удобном виде. Однако в задачах по термодинамике часто может потребоваться несколько иной вид. Ниже записаны еще три формулы, которые непосредственно следуют из записанного уравнения:

Эти три уравнения также являются универсальными для идеального газа, только в них появляются такие величины, как масса m, молярная масса M, плотность ρ и число частиц N, которые составляет систему. Символом kB здесь обозначена постоянная Больцмана (1,38*10-23 Дж/К).

Закон Бойля-Мариотта

Когда Клапейрон составлял свое уравнение, то он основывался на газовых законах, которые были открыты экспериментально несколько десятилетий ранее. Одним из них является закон Бойля-Мариотта. Он отражает изотермический процесс в закрытой системе, в результате которого изменяются такие макроскопические параметры, как давление и объем. Если положить T и n постоянными в уравнении состояния идеального газа, газовый закон тогда примет вид:

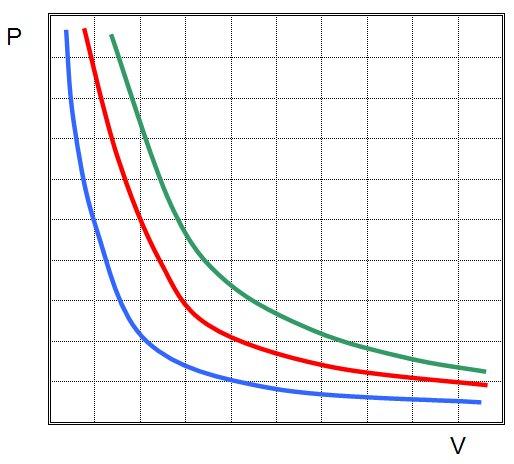
Это и есть закон Бойля-Мариотта, который говорит о том, что произведение давление на объем сохраняется во время произвольного изотермического процесса. При этом сами величины P и V изменяются.

Если изображать график зависимости P(V) или V(P), то изотермы будут представлять собой гиперболы.

Законы Шарля и Гей-Люссака

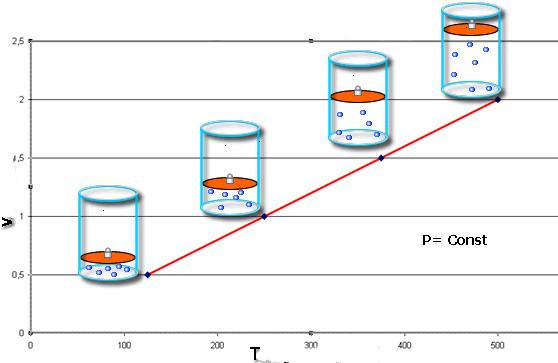
Эти законы математически описывают изобарный и изохорный процессы, то есть такие переходы между состояниями газовой системы, при которых сохраняются давление и объем, соответственно. Закон Шарля математически можно записать следующим образом:

V/T = const при n, P = const.

Закон Гей-Люссака записывается так:

P/T = const при n, V = const.

Если оба равенства представить в виде графика, то мы получим прямые линии, которые под некоторым углом наклонены к оси абсцисс. Такой вид графиков говорит о прямой пропорциональности между объемом и температурой при постоянном давлении и между давлением и температурой при постоянном объеме.

Отметим, что все три рассмотренных газовых закона не принимают во внимание химический состав газа, а также изменение его количества вещества.

Абсолютная температура

В быту мы привыкли пользоваться температурной шкалой Цельсия, поскольку она является удобной для описания окружающих нас процессов. Так, вода кипит при температуре 100 oC, а замерзает при 0 oC. В физике эта шкала оказывается неудобной, поэтому применяют так называемую абсолютную шкалу температур, которая была введена лордом Кельвином в середине XIX века. В соответствии с этой шкалой температура измеряется в Кельвинах (К).

Помимо приведенного выше физического смысла абсолютной температуры, существуют другие подходы к пониманию этой величины. Одним из них является упомянутый газовый закон Шарля. Запишем его в следующей форме:

Последнее равенство говорит о том, что при определенном количестве вещества в системе (например, 1 моль) и определенном давлении (например, 1 Па) объем газа однозначно определяет абсолютную температуру. Иными словами, возрастание объема газа при указанных условиях возможно только за счет увеличения температуры, а уменьшение объема свидетельствует об уменьшении величины T.

Напомним, что в отличие от температуры по шкале Цельсия, абсолютная температура не может принимать отрицательные значения.

Принцип Авогадро и газовые смеси

Помимо изложенных выше газовых законов, уравнение состояния для идеального газа также приводит к открытому Амедео Авогадро в начале XIX века принципу, который носит его фамилию. Этот принцип устанавливает, что объем любого газа при постоянных давлении и температуре определяется количеством вещества в системе. Соответствующая формула выглядит так:

n/V = const при P, T = const.

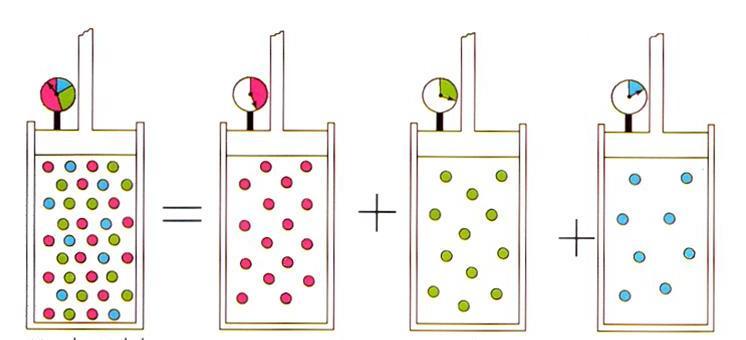
Записанное выражение приводит к известному в физике идеальных газов закону Дальтона для газовых смесей. Этот закон гласит, что парциальное давление газа в смеси однозначно определяется его атомной долей.

Пример решения задачи

В закрытом сосуде с жесткими стенками, содержащем идеальный газ, в результате нагревания давление увеличилось в 3 раза. Необходимо определить конечную температуру системы, если ее начальное значение было равно 25 oC.

Сначала переведем температуру из градусов Цельсия в Кельвины, имеем:

T = 25 + 273,15 = 298,15 К.

Поскольку стенки сосуда являются жесткими, то процесс нагревания можно считать изохорным. Для этого случая применим закон Гей-Люссака, имеем:

Таким образом, конечная температура определяется из произведения отношения давлений и начальной температуры. Подставляя в равенство данные, получаем ответ: T2 = 894,45 К. Эта температура соответствует 621,3 oC.

Источник

Основное уравнение МКТ идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Идеальный газ — газ, удовлетворяющий трем условиям:

Реальный газ с малой плотностью можно считать идеальным газом.

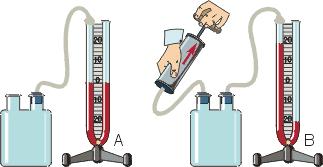
Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

Если особо важна точность, следует использовать более точную формулу:

Пример №1. Температура воды равна o C. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p — давление идеального газа, n — концентрация молекул газа, − E k — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

m 0 — масса одной молекулы газа;

n — концентрация молекул газа;

− v 2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

k — постоянная Больцмана (k = 1,38∙10 –3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

Температура — мера кинетической энергии молекул идеального газа:

Полная энергия поступательного движения молекул газа определяется формулой:

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Составим систему уравнений:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Источник

Как узнать абсолютную температуру газа

7. Идеальный газ. Основное уравнение МКТ идеального газа. Температура и ее измерение. Абсолютная температура

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если: а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела; б) газ очень, разрежен, т. е. расстояние между молекулами намного больше размеров самих молекул; в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел овойства идеального, осуществляются при соответстсвующем разрежении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление, объем и температура.

Одним из первых и важных успехов МКТ было Качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается и том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.

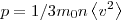
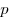
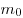
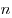
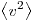
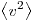
На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: , где — давление идеального газа, — масса молекулы, — концентрации молекул, — среднее значение квадрата скоростой молекул. Если представить себе фантастическую ситуацию, в которой нам известны скорости всех молекул и единице объема, то можно было бы вычислить по формуле

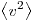
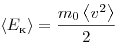
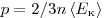
Величина позволяет ввести представление о сродной кинетической энергии поступательного движения молекул идеального газа . Тогда основное уравнение МКТ идеального газа можно записать в виде: .

Однако, измерив только давление газа, невозможно уанатъ ни среднее значение кинетической энергии молекул по отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметром газа нужно измерение еще какойто физической величины, связанной со средней кинетической энергией молекул. Такой величиной является температура. Температура — скалярная физическая величина, описывающая состояние термодинамического равновесия (состояния, при котором не происходит изменения микроскопических параметров). 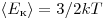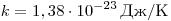Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого за нулевое, как молекулярно-кинетическая величина — характеризует интенсивность хаотического движения молекул, измеряется их средней кинетической энергией: где и называется постоянной Больцмана.

Температура всех частей изолированной системы находящейся в равновесии, одинакова. Измеряется температура термометрами в градусах различных температурных шкал. Существует абсолютная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличаются начальными точками. До введения абсолютной шкалы температур в практике широкое распространение получила шкала Цельсия (за О°С принята точка замерзания воды, за 100°С принята точка кипения воды при нормальном атмосферном давлении).

1. Не всегда правильно объясняют экзаменуемые различие между идеальными и реальными газами. Были, например, такие ответы: «Идеальный газ — это реальный газ без примесей», «Идеальный газ — это реальный газ при низкой температуре» и т. п.

Слово «идеальный» означает «воображаемый, реально не существующий». Реальный газ отличется от идеального наличием взаимодействия молекул. При малых плоностях в нем преобладают силы притяжения, что приводит к появлению дополнительного давления: газ как бы сжимает сам себя. При больших плотностях действуют силы отталкивания, вследтсвие чего молекула не допускает проникновения других молекул в занимаемый ею объем. Пренебрегать собственным объемом молекул реального газа нельзя.

При не слишком высоком давлении (например, при атмосферном) и не слишком низкой температуре (например, при комнатной) реальный газ с достаточной степенью точности подчиняется законам идеального газа.

Источник

Как сказал.

Жизнь — как вождение велосипеда. Чтобы сохранить равновесие, ты должен двигаться

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 15. Лекция 15. Идеальный газ

Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.

Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:

Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.

Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.

Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.

Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.

Модель идеального газа. Связь между давлением и средней кинетической энергией.

Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.

Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)

Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.

Свойства идеального газа:

Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.

Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.

До настоящего времени употребляются внесистемные единицы давления:

техническая атмосфера 1 ат = 9,81-104 Па;

физическая атмосфера 1 атм = 1,013-105 Па;

миллиметры ртутного столба 1 мм рт. ст.= 133 Па;

1 атм = = 760 мм рт. ст. = 1013 гПа.

Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени дей­ствует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.

Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.

Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.

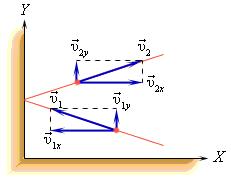
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ_y скорости, параллельная стенке, остается неизменной.

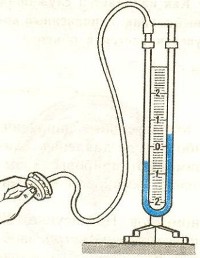
Приборы, измеряющие давление, называют манометрами. Манометры фиксиру­ют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

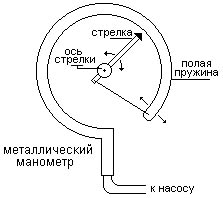
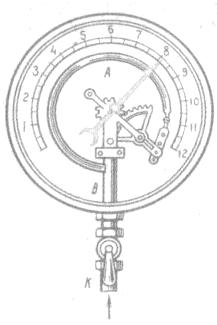
Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.

Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул

n = N/V – число молекул в единице объема, или концентрация молекул;

Так как средняя кинетическая энергия поступательного движения молекул E = m₀*v 2 /2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m₀· v 2 )/2 = 2/3·E·n

Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.

Так как m₀·n = m₀·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v 2

Объединенный газовый закон.

Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.

Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.

Всякое изменение состояния газа называется термодинамическим процессом.

В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.

Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.

Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.

Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

где n – концентрация молекул, N – общее число молекул, V – объем газа

Тогда получим 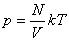или

Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит

При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.

Уравнение Клайперона можно записать в другой форме.

Здесь N – число молекул в сосуде, ν – количество вещества, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.

Ее численное значение в СИ R = 8,31 Дж/моль·К

называется уравнением состояния идеального газа.

В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`

Для одного моля любого газа это соотношение принимает вид: pV=RT

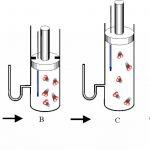
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.

Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)

ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:

pS = F – сила давления.

Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.

Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.

Источник