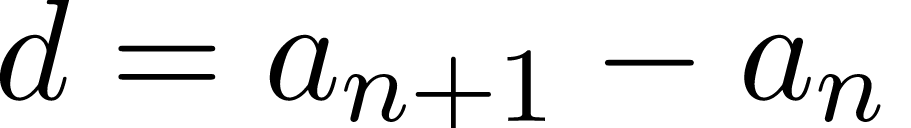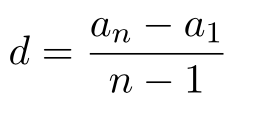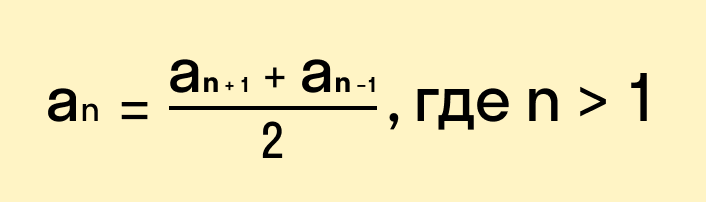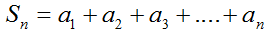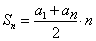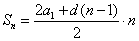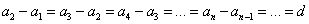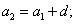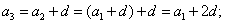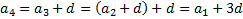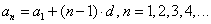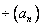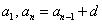как узнать д в арифметической прогрессии

Как вычислить арифметическую прогрессию

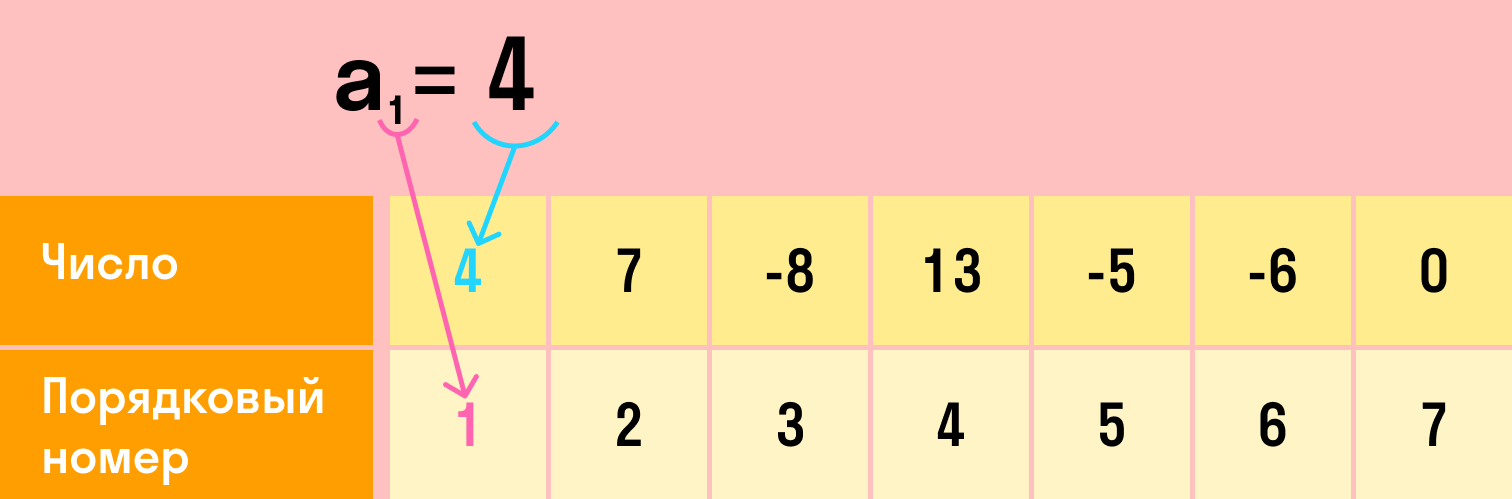
Арифметическая прогрессия — основные понятия

Арифметическая прогрессия — это монотонная последовательность, которая состоит из ряда чисел.

В этом ряду каждое последующее число есть результат добавления к предыдущему одного и того же числа d. В случае, если \(d\;>\;0,\) последовательность называется возрастающей, а если \(d\; — убывающей. В ситуации, если d = 0 последовательность стационарна.

Наиболее простым примером арифметической прогрессии будет являться бесконечная последовательность натуральных чисел.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Число d является разностью арифметической прогрессии или шагом, а числа последовательности — членами прогрессии.

Последовательность \(\) будет являться арифметической прогрессией исключительно в тех случаях, когда любой ее член, начиная со второго, будет равняться полусумме последующего и предыдущего членов:

Если говорить об арифметической прогрессии, то для всех n = 2, 3. справедливо:

Вычисление каждого следующего члена арифметической прогрессии возможно с использованием следующей формулы:

Формула общего члена для расчета любого из членов прогрессии выглядит следующим образом:

Общий вид арифметической прогрессии

Арифметической прогрессией называют числовую последовательность, которая имеет следующий вид:

Каждую арифметическую прогрессию можно задать формулой вида:

Свойства и формулы арифметической прогрессии

Разность арифметической прогрессии вычисляется по следующей формуле:

Существует несколько формул для нахождения членов арифметической прогрессии с номером n:

В обоих случаях \(a_1\) будет обозначать первый член прогрессии, d здесь будет являться разностью прогрессии, а a_m обозначает член арифметической прогрессии с номером m.

Сумма первых членов арифметической прогрессии вычисляется с использованием следующих формул:

В данной формуле \(a_1\) является обозначением первого члена прогрессии, \(a_n\) — обозначением члена прогрессии с номером n, а n — обозначением суммируемых членов прогрессии.

Дополнительно к предыдущим обозначениям в этой формуле d — это шаг прогрессии, а n — число суммируемых членов прогрессии.

Вывод этой формулы выглядит следующим образом:

Предоставим объяснение того, что выражения, заключенные в скобки, равны как между собой, так и выражению \(a_1 + a_n\) :

Тогда мы можем записать:

Из этого выводится формула, дающая в результате сумму первых n членов арифметической прогрессии:

Еще одно свойство арифметической прогрессии — сходность. Арифметическая прогрессия будет являться расходящейся при \(d\;\neq0\) и сходящейся при d = 0.

Арифметическая прогрессия второго порядка

Последовательность чисел, при которой последовательность разностей образует арифметическую прогрессию, будет называться арифметической прогрессией второго порядка.

Сумма квадратов арифметической прогрессии

Источник

Арифметическая прогрессия.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Понятие арифметической прогрессии.

Я напишу незаконченный ряд чисел:

Сможете продлить этот ряд? Какие числа пойдут дальше, за пятёркой? Каждый. э-э-э. короче, каждый сообразит, что дальше пойдут числа 6, 7, 8, 9 и т.д.

Усложним задачу. Даю незаконченный ряд чисел:

Сможете уловить закономерность, продлить ряд, и назвать седьмое число ряда?

А теперь переведём ключевые моменты из ощущений в математику.)

Первый ключевой момент.

Арифметическая прогрессия имеет дело с рядами чисел. Это и смущает поначалу. Мы привыкли уравнения решать, графики строить и всё такое. А тут продлить ряд, найти число ряда.

Второй ключевой момент.

В арифметической прогрессии любое число отличается от предыдущего на одну и ту же величину.

Третий ключевой момент.

Этот момент не бросается в глаза, да. Но очень, очень важен. Вот он: каждое число прогрессии стоит на своём месте. Есть первое число, есть седьмое, есть сорок пятое, и т.д. Если их перепутать как попало, закономерность исчезнет. Исчезнет и арифметическая прогрессия. Останется просто ряд чисел.

Разумеется, в новой теме появляются новые термины и обозначения. Их надо знать. Иначе и задание-то не поймёшь. Например, придётся решать, что-нибудь, типа:

Термины и обозначения.

Эта величина называется разность арифметической прогрессии. Разберёмся с этим понятием поподробнее.

Разность арифметической прогрессии.

Один важный момент. Прошу обратить внимание на слово «больше». Математически это означает, что каждое число прогрессии получается прибавлением разности арифметической прогрессии к предыдущему числу.

Разность арифметической прогрессии может быть положительной, тогда каждое число ряда получится реально больше предыдущего. Такая прогрессия называется возрастающей. Например:

Здесь каждое число получается прибавлением положительного числа, +5 к предыдущему.

Разность может быть и отрицательной, тогда каждое число ряда получится меньше предыдущего. Такая прогрессия называется (вы не поверите!) убывающей.

Разность арифметической прогрессии обозначается, как правило, буквой d.

Определим, например, d для возрастающей арифметической прогрессии:

Берём любое число ряда, какое хотим, например, 11. Отнимаем от него предыдущее число, т.е. 8:

Это правильный ответ. Для этой арифметической прогрессии разность равна трём.

Определим d для убывающей арифметической прогрессии:

Разность арифметической прогрессии может быть любым числом: целым, дробным, иррациональным, всяким.

Другие термины и обозначения.

Каждое число ряда называется членом арифметической прогрессии.

Как записать прогрессию в общем виде? Не вопрос! Каждое число ряда записывается в виде буквы. Для обозначения арифметической прогрессии используется, как правило, буква a. Номер члена указывается индексом внизу справа. Члены пишем через запятую (или точку с запятой), вот так:

Прогрессии бывают конечные и бесконечные.

Записать конечную прогрессию через ряд можно вот так, все члены и точка в конце:

Или так, если членов много:

В краткой записи придётся дополнительно указывать количество членов. Например (для двадцати членов), вот так:

Бесконечную прогрессию можно узнать по многоточию в конце ряда, как в примерах этого урока.

Теперь уже можно порешать задания. Задания несложные, чисто для понимания смысла арифметической прогрессии.

Примеры заданий по арифметической прогрессии.

Разберём подробненько задание, что приведено выше:

Легко можно посчитать, например, a₃. Мы знаем (по смыслу арифметической прогрессии), что a₃ больше a₂ на величину d. Стало быть:

Ну и дальше, по накатанной колее:

Так, члены с третьего по шестой вычислили. Получился такой ряд:

Остаётся найти первый член a₁ по известному второму. Это шаг в другую сторону, влево.) Значит, разность арифметической прогрессии d надо не прибавить к a₂, а отнять:

Вот и все дела. Ответ задания:

Попутно замечу, что это задание мы решали рекуррентным способом. Это страшное слово означает, всего лишь, поиск члена прогрессии по предыдущему (соседнему) числу. Другие способы работы с прогрессией мы рассмотрим далее.

Из этого несложного задания можно сделать один важный вывод.

Если нам известен хотя бы один член и разность арифметической прогрессии, мы можем найти любой член этой прогрессии.

Запомнили? Этот несложный вывод позволяет решать большинство задач школьного курса по этой теме. Все задачи крутятся вокруг трёх главных параметров: член арифметической прогрессии, разность прогрессии, номер члена прогрессии. Всё.

Для примера рассмотрим некоторые популярные задания по этой теме.

2. Запишите конечную арифметическую прогрессию в виде ряда, если n=5, d = 0,4, и a₁ = 3,6.

Здесь всё просто. Всё уже дано. Нужно вспомнить, как считаются члены арифметической прогрессии, посчитать, да и записать. Желательно не пропустить слова в условии задания: «конечную» и «n=5«. Чтобы не считать до полного посинения.) В этой прогрессии всего 5 (пять) членов:

Остаётся записать ответ:

3. Определите, будет ли число 7 членом арифметической прогрессии (a_n), если a₁ = 4,1; d = 1,2.

Хм. Кто ж его знает? Как определить-то?

Как-как. Да записать прогрессию в виде ряда и посмотреть, будет там семёрка, или нет! Считаем:

Так, стоит считать дальше, или нет, как думаете?) Разумеется, нет! Запишем в виде ряда:

Сейчас чётко видно, что семёрку мы просто проскочили между 6,5 и 7,7! Не попала семёрка в наш ряд чисел, и, значит, семёрка не будет членом заданной прогрессии.

А вот задачка на основе реального варианта ГИА:

4. Выписано несколько последовательных членов арифметической прогрессии:

Найдите член прогрессии, обозначенный буквой х.

Здесь записан ряд без конца и начала. Нет ни номеров членов, ни разности d. Ничего страшного. Для решения задания достаточно понимать смысл арифметической прогрессии. Смотрим и соображаем, что можно узнать из этого ряда? Какие параметры из трёх главных?

Номера членов? Нет тут ни единого номера.

Остались сущие пустяки. Какое число будет предыдущим для икса? Пятнадцать. Значит, икс можно легко найти простым сложением. К 15 прибавить разность арифметической прогрессии:

Вот и всё. Ответ: х=12

6. Известно, что число 5,5 является членом арифметической прогрессии (a_n), где a₁ = 1,6; d = 1,3. Определите номер n этого члена.

7. Известно, что в арифметической прогрессии a₂ = 4; a₅ = 15,1. Найдите a₃.

8. Выписано несколько последовательных членов арифметической прогрессии:

Найдите член прогрессии, обозначенный буквой х.

9. Поезд начал движение от станции, равномерно увеличивая скорость на 30 метров в минуту. Какова будет скорость поезда через пять минут? Ответ дайте в км/час.

Ответы (в беспорядке): 7,7; 7,5; 9,5; 9; 0,3; 4.

Всё получилось? Замечательно! Можно осваивать арифметическую прогрессию на более высоком уровне, в следующих уроках.

Не всё получилось? Не беда. В Особом разделе 555 все эти задачки разобраны по косточкам.) И, конечно, описан простой практический приём, который сразу высвечивает решение подобных заданий чётко, ясно, как на ладони!

В этом уроке мы рассмотрели элементарный смысл арифметической прогрессии и её основные параметры. Этого достаточно для решения практически всех задач на эту тему. Прибавляй d к числам, пиши ряд, всё и решится.

Решение «на пальцах» хорошо подходит для очень коротких кусочков ряда, как в примерах этого урока. Если ряд подлиннее, вычисления усложняются. Например, если в задачке 9 в вопросе заменить «пять минут» на «тридцать пять минут», задачка станет существенно злее.)

А ещё бывают задания простые по сути, но несусветные по вычислениям, например:

Дана арифметическая прогрессия (a_n). Найти a₁₂₁, если a₁=3, а d=1/6.

И что, будем много-много раз прибавлять по 1/6?! Это же убиться можно!?

Можно.) Если не знать простую формулу, по которой решать подобные задания можно за минуту. Эта формула будет в следующем уроке. И задачка эта там решена. За минуту.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Арифметическая прогрессия свойства и формулы

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

«Последовательность простых чисел: 4, 6, 10, 19, 21, 33. »

Последовательность y_n = C называют постоянной или стационарной.

Арифметическая прогрессия — (a_n), задана таким соотношением:
a₁ = a, a_n+1= a_n + d.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.