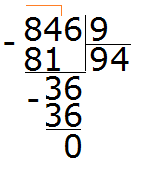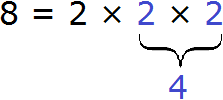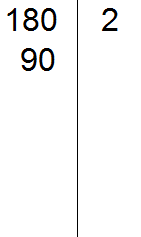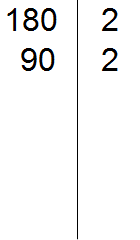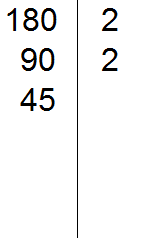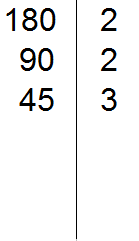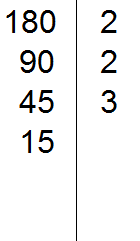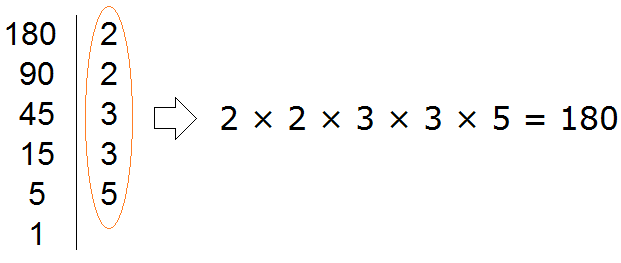как узнать делители числа
Как узнать все делители числа?
Как найти простые делители числа?
Чтобы найти все делители числа a нужно:
Какие делители у числа 72?
Семьдесят дваСумма цифр9Произведение цифр14Произведение цифр (без учета ноля)14Все делители числа1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72Наибольший делитель из ряда степеней двойки8Ещё 33 строки
Что такое натуральный делитель числа?
Определение. Любое натуральное число, на которое делится (без остатка) данное натуральное число, называется делителем данного числа. Любое натуральное число, которое делится (без остатка) на данное натуральное число, называется кратным данному числу.
Как найти частное чисел?
Определение частного чисел
Как найти самый большой делитель числа?
Наибольший общий делитель
Что такое делители и кратные числа?
Если одно из натуральных чисел делится без остатка на другое, то первое число называется кратным второго, а второе — делителем первого. … Число, которое имеет только два делителя, называется простым.
Как узнать может ли число быть кратно?
Какие делители числа 68?
Делители числа 68: 1, 2, 4, 17, 34, 68. 126 — сумма делителей. 68 и 0.014705882352941176 являются взаимно обратными числами. Перевод числа в другие системы счисления: двоичная система счисления: 1000100, троичная система счисления: 2112, восьмеричная система счисления: 104, шестнадцатеричная система счисления: 44.
Какое число в квадрате равно 72?
То есть таких числа 2. Это логично, потому что при возведении в квадрат число, даже будучи неположительным, становится положительным. Ответ: sikringbp и 2 других пользователей посчитали ответ полезным!
Сколько делителей у числа 16?
У числа 16 5 делителей: 1, 2, 4, 8, 16. Обратное число к 16 – это 0.0625. Данное число представляется произведением: 2 * 2 * 2 * 2. Число в других системах счисления: двоичная система счисления: 10000, троичная система счисления: 121, восьмеричная система счисления: 20, шестнадцатеричная система счисления: 10.
Сколько делителей у числа 48?
Сорок восемьСумма цифр12Все делители числа1, 2, 3, 4, 6, 8, 12, 16, 24, 48Наибольший делитель из ряда степеней двойки16Количество делителей10Сумма делителей124Ещё 32 строки
Что называется делителем числа?
Чему равны наибольший общий делитель и наименьшее общее кратное взаимно простых чисел? а) Делителем данного числа называют такое число, на которое делится данное. Кратным называется такое число, которое делится на данное без остатка. Например, 2 — делитель 8; 32 — кратное 16.
Что такое делитель пример?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. … Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Делители и кратные
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
Определение. Кратным числа а называется число, которое делится без остатка на а.
Кратным числа 5 называется число, которое делится без остатка на 5 .
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
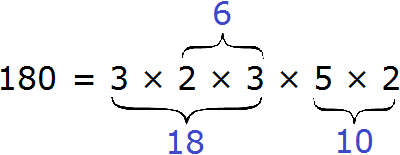
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
Теперь раскладываем множители 18 и 10 на другие множители:
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
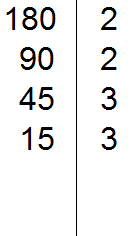
Проводим вертикальную линию и слева записываем первое делимое 180
Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
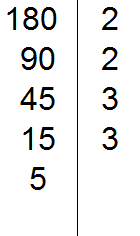
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
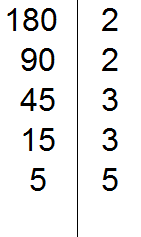
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
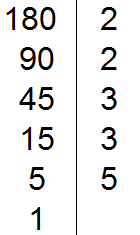
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
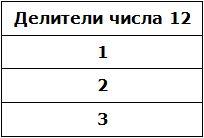
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1
Теперь раскладываем число 12 на простые множители:
Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
Занесём число 4 в нашу таблицу делителей
Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:
Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
1, 2, 3, 6
Кратное и делитель
Если одно натуральное число делится без остатка на другое натуральное число, то первое называется кратным второго, а второе — делителем первого.
Кратное числа — это делимое, которое делится на данный делитель без остатка.
Делитель числа — это делитель, на который делимое делится без остатка.
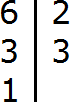
Пример. Возьмём, например, такое деление:
Число 6 делится на число 3 без остатка. Следовательно, число 6 — кратное числа 3, а число 3 — делитель числа 6.
Пусть m и n — натуральные числа, если число m является кратным числа n, то говорят: m кратно n или m делится на n
Пример. 6 кратно 3 (шесть кратно трём) или 6 делится на 3 (шесть делится на три).
Самым маленьким кратным любого натурального числа является само это число, так как любое натуральное число можно разделить само на себя без остатка (в частном всегда будет единица).
Пример. Для числа 7 наименьшим кратным является число 7, для числа 2 — число 2:
7 : 7 = 1 (семь кратно семи);
2 : 2 = 1 (два кратно двум).
Для любого натурального числа существует бесконечно много кратных. Получить кратное для данного числа достаточно легко, можно просто умножить его на любое натуральное число, полученное произведение и будет его кратным.
Пример. Получим кратное числа 5, умножив его, например, на 2:
Число 10 — кратное числа 5:
Так как на единицу делится любое натуральное число, то число 1 является делителем любого натурального числа.
Найти количество делителей числа
Учеников часто просят найти количество делителей числа, но в действительности это полезно не только для учащихся. Подобные вычисления помогают быстро выяснить, как распределить значительный объём чего-то на несколько равных частей. К тому же можно узнать, сколько именно таких равных частей вообще может быть.
Заниматься поиском всех делителей числа в реальной жизни нередко приходится бухгалтерам и руководителям предприятий, когда они распределяют поступившую прибыль. Такие же расчёты очень полезны для самопроверки тем, кто постоянно имеет дело с разными вычислениями. Например, в строительстве при создании какого-нибудь проекта. Или же при проведении разных экспериментов, как теоретических, так и практических.
А кому ещё нужно искать количество делителей числа?
С этими расчётами периодически сталкиваются студенты, особенно если для них математика не относится к профильным предметам. Такие вычисления делают, разумеется, и преподаватели при проверке работ. Им нередко приходится обрабатывать большое количество домашних заданий, контрольных, курсовых. И всего вычислений оказывается столько, что в них очень легко запутаться. В такой ситуации калькулятор поможет проверить себя.
Программа нужна далеко не только тем, кто не умеет находить делители самостоятельно. В первую очередь она помогает тем, кто сильно загружен и может пропустить ошибку просто из-за большого объёма работы.
Какие ещё математические калькуляторы на нашем сайте вам пригодятся?
На нашем сайте опубликовано множество математических программ, которые вам могут пригодиться. Например, калькулятор квадратных корней позволяет быстро извлечь корень квадратный из числа. Конечно, справится с такой задачей без особых проблем может большинство школьников. Однако задание усложняется, если речь идёт о большом числе. И ещё легче запутаться, когда за запятой оказывается много цифр. А благодаря калькулятору вы получите точный результат, причём быстро.
А вот разница в процентах поможет сравнить между собой 2 разные величины в ситуации, когда что-то меняется. Например, у предпринимателя может скакать от месяца к месяцу прибыль. Причём это вполне вероятно по разным точкам или по разным источникам поступления прибыли. В такой ситуации очень важно увидеть тенденцию, быстро сделать расчёты, чтобы понять, что предпринимать дальше.
Преимущество калькуляторов в том, что они позволяют не тратить время. Сделать множество расчётов можно буквально за несколько минут. И при этом программы были неоднократно проверены. В правильности расчётов можно не сомневаться.
Как найти общее количество делителей числа?
Воспользоваться калькулятором довольно просто. Для этого достаточно указать какое-то число, которое вас интересует. А потом – нажать на кнопку для расчёта. Но обратите внимание на то, что число в любом случае должно быть целым.
Результат появится наверху, на зелёном фоне. При этом вы увидите перечисление делителей, а также указание их общего количества. Данные можно сохранить в файл, скопировать (как саму информацию, так и ссылку на результат расчётов). Кроме того, сведения можно вывести на печать.
Также есть кнопка «запомнить». Благодаря ей вы увидите результат, когда зайдёте в очередной раз на сайт под своим аккаунтом.
Вычисления проводятся очень быстро. Ждать не придётся: результат появится мгновенно! При этом пользоваться калькулятором можно с любого устройства, вне зависимости от того, идёт ли речь о планшете или о смартфоне.
Нахождение всех делителей числа, число делителей числа.
Материал этой статьи про нахождение всех делителей числа. Сначала доказана теорема, которая задает вид всех общих делителей данного числа, после чего рассмотрены примеры нахождения всех делителей. Дальше показано, как вычисляется число делителей числа. В заключение подробно разобраны примеры нахождения всех общих делителей нескольких чисел и их количества.
Навигация по странице.
Все делители числа, их нахождение
Дальнейшее изложение подразумевает хорошее владение информацией статьи делители и кратные числа. Мы будем говорить лишь о поиске всех делителей целых положительных чисел (натуральных чисел). Этого вполне достаточно, так как одно из свойств делимости утверждает, что множество делителей целого отрицательного числа −a совпадает со множеством делителей противоположного числа a (которое будет положительным). Напомним также, что число 0 имеет бесконечно много делителей, и нахождение всех делителей нуля не представляет интереса.
Интереснее проходит поиск всех делителей составных чисел. Теоретическая основа этого процесса заключается в следующей теореме.
Из рассмотренной теоремы следует алгоритм нахождения всех положительных делителей данного числа. Чтобы найти все делители числа a нужно:
Весь процесс нахождения делителей удобно проводить, заполняя таблицу следующего вида:
Сначала разложим на простые множители число 567 :
Еще немного усложним пример.
Число делителей числа
Разложим 84 на простые множители:
число 84 имеет 24 делителя.
Нахождение всех общих делителей чисел и их количества
Из свойств наибольшего общего делителя следует, что множество делителей данных целых чисел совпадает со множеством делителей НОД этих чисел. Это утверждение относится как к двум числам, так и к трем, и к большему их количеству. Таким образом, чтобы найти все общие делители данных чисел, нужно определить НОД этих чисел и найти все его делители.
Рассмотрим решения примеров, в которых находятся все общие делители некоторых чисел.