как узнать диагональ прямоугольника по двум сторонам калькулятор

Диагональ прямоугольника

Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.

Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.

Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.

Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.

Как найти диагональ прямоугольника

Воспользуемся теоремой Пифагора и формулой

d — диагональ квадрата

a — длина прямоугольника

b — ширина прямоугольника

Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.

Диагональ прямоугольника онлайн калькулятор

Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.

Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.

Источник

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

где \( \small a \) и \( \small b \) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем \( \small b \) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

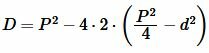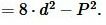(11)

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Источник

Стороны прямоугольника

Свойства

Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить. P=2(a+b)

Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу. S=ab

Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1) d_1=d_2=√(a^2+b^2 )

Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов. α=arc tan⁡〖b/a〗 β=arc tan⁡〖a/b〗

Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2) γ=2α δ=2β

Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3) R=d/2=√(a^2+b^2 )/2

Источник

Периметр и диагональ прямоугольника

Свойства

Зная периметр прямоугольника и его диагональ можно составить систему уравнений с двумя неизвестными, благодаря которой становится возможным решить задачу методом подстановки. (Рис.56.1) <█(P=2(a+b)@a^2+b^2=d^2 )┤

Чтобы решить такую систему, необходимо выразить одну сторону из первого уравнения. P=2(a+b) P=2a+2b 2a=P-2b a=P/2-b

Теперь полученное выражение для переменной «a» подставляем во второе уравнение и находим значение переменной «b». (P/2-b)^2+b^2=d^2 〖P^2/4-Pb+b^2+b〗^2=d^2 〖2b〗^2-Pb+P^2/4-d^2=0

Получилось квадратное уравнение, для решения которого нужно найти дискриминант. D=b^2-4ac=P^2-4*2*(P^2/4-d^2 )=P^2-2P^2+8d^2=8d^2-P^2

В данном уравнении при значении дискриминанта больше либо равном нулю 8d^2-P^2 ≥ 0, будет два решения. Это и будут обе стороны прямоугольника x=(-b±√(b^2-4ac))/2a b=(P+√(8d^2-P^2 ))/4 a=(P-√(8d^2-P^2 ))/4

Углы пересечения диагоналей со сторонами α и β можно найти из соотношения сторон в прямоугольном треугольнике, образованном диагональю. Тангенс угла α равен отношению b к a, а тангенс угла β равен отношению a к b. α=arc tan⁡〖b/a〗 β=arc tan⁡〖a/b〗

Вертикальные углы при пересечении диагоналей можно вычислить, удвоив величины углов α и β, как видно из рисунка. (рис. 56.2) γ=2α δ=2β

Радиус описанной окружности прямоугольника через диагональ вычисляется делением ее на два, так как точка пересечения диагоналей, которая является центром окружности, делит диагонали на две равные части – радиусы (рис. 56.3) R=d/2

Источник

Диагональ и сторона «А» прямоугольника

Свойства

В прямоугольнике диагональ со сторонами образует прямоугольный треугольник, который связывает все их значения вместе теоремой Пифагора. Поэтому неизвестную сторону можно выразить как квадратный корень из разности квадрата диагонали и квадрата известной стороны. (рис. 56.1) b=√(d^2-a^2 )

Тогда периметр прямоугольника и его площадь теперь будут зависеть только от одной стороны и диагонали, которые используя это выражение, можно подставить в любую необходимую формулу. P=2(a+b)=2(a+√(d^2-a^2 )) S=ab=a√(d^2-a^2 )

Угол пересечения диагонали со стороной зависит от отношения одной стороны к другой, которое образует тангенс искомого угла. Таким образом, меняя положение сторон в отношении, через арктангенс можно найти угол α и угол β. Опять же, вместо неизвестной стороны будет разность квадратов диагонали и стороны под корнем. α=arc tan⁡〖b/a〗=arc tan⁡〖√(d^2-a^2 )/a〗 β=arc tan⁡〖a/b〗=arc tan⁡〖a/√(d^2-a^2 )〗

Углы пересечения самих диагоналей делятся на две части, каждая из которых равна углу α или β з прямоугольного треугольника образованного полуосью симметрии прямоугольника. Поэтому, умножив нужный угол на 2, получим центральный угол прямоугольника. (рис. 56.2) γ=2α δ=2β

Также, зная диагональ, можно вычислить радиус описанной окружности. Диагонали в точке пересечения дают центр прямоугольника, который является и центром окружности. Соответственно радиус совпадает с диагональю, и равен ее половине. (рис. 56.3) R=d/2

Источник