как узнать диаметр круга если известна площадь

Как найти диаметр окружности

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как апельсин 🍊 и тарелка.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Записывайтесь на курсы по математике для учеников с 1 по 11 классы.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Источник

Площадь круга: как найти, формулы

площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ

Определение основных понятий

Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как глобус и мяч.

Формула вычисления площади круга

Давайте разберем несколько формул расчета площади круга. Поехали!

Площадь круга через радиус

Площадь круга через диаметр

S = π × d 2 : 4, где d — это диаметр.

Площадь круга через длину окружности

S = L 2 ​ : (4 × π), где L — это длина окружности.

Популярные единицы измерения площади:

Задачи. Определить площадь круга

Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!

Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.

Диаметр окружности равен двум радиусам.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 12 2 : 4.

Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 90 2 : 4.

Задание 3. Найти длину окружности при радиусе 3 см.

Отношение длины окружности к диаметру является постоянным числом.

Получается: L = d × π.

Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.

Подставим значение радиуса: L = 2 × 3,14 × 3.

Источник

Длина окружности

6 класс, 9 класс, ЕГЭ/ОГЭ

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

π— число пи — математическая константа, равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, равное 3,14

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, равное 3,14

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она всегда равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Источник

Площадь круга

Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:

S=πr 2 – это произведение числа пи на квадрат радиуса.

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .

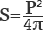
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.

Источник

Калькуляторы и формулы диаметра круга.

Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга

Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его.

Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.

Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π.

Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.

Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра.

Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.

Что такое длина окружности?

После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.

Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.

Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.

Формула вычисления длины/периметра

1. Через радиус

Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:

C = 2 * π * r

Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.

2. Через диаметр

Периметр/длина окружности считается как произведение ее диаметра на число π:

C = π * d

Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.

Примечание: в расчетах значение числа π округляется до 3,14.

Вычисление площади круга и длины окружности, когда радиус или диаметр выражены переменными

Найдите радиус или диаметр окружности.

В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.

Напишите формулу с данным значением.

Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.

Напишите формулу: C = 2πr

Вычислите длину окружности так, как если бы переменная была представлена числом.

На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.

C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28

Попрактикуйтесь на нескольких примерах.

Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.

Как измерить диаметр трубы

При укладке трубопроводов монтажникам приходится сталкиваться с различными вариантами их расположения, от этого нередко зависит, как измеряется труба. Для нахождения нужных параметров в бытовых условиях обычно используют любой измерительный инструмент, находящийся под руками, и при необходимости простую формулу расчета.

На производстве измерения в основном для контроля проводятся более сложным высокоточным инструментом или приборами (используется например лазерный измеритель линейка циркометр).

Рис. 12 Способы монтажа фитингов на РЕХ-трубы: компрессионный, натяжными муфтами, пресс-фитингами, пуш-фитингами

Как измерить диаметр трубы линейкой и рулеткой

Рулетку или линейку практически всегда можно обнаружить в бытовом хозяйстве, с их помощью узнают параметры разрезанной поперек трубы. Для определения размеров инструменты прикладывают к трубному торцу и смотрят на их шкалу, визуально сопоставляя ее показания с сечением изделия. Точность данного способа невелика — измерения сложно проводить точно по диагонали.

Если коммуникации располагаются в труднодоступных местах и не обрезаны, точно определить диаметр трубы рулеткой или с помощью линейки становится слишком сложно. К стене вокруг трубной оболочки придется прикладывать с двух сторон прямоугольные детали и измерять расстояние между ними максимально близко к оболочке для снижения погрешности.

Рис. 13 Как измерить диаметр трубы рулеткой и линейкой

При помощи штангенциркуля

Штангенциркуль является довольно удобным измерительным инструментом для определения внутренних и наружных размеров в окружности до 150 мм с точностью от 0,1 мм. Современные приборы помимо механической шкалы, могут иметь электронную или стрелочную индикацию.

Штангенциркулем удобно измерять трубопровод в труднодоступных местах, соприкасающийся или даже частично размещенный в стене, стяжке менее чем наполовину. Точность показаний в 0,1 мм вполне приемлема для любых хозяйственных целей.

Еще более точные показания можно получить при использовании микрометра, однако если штангенциркуль изредка встречаются в домашнем хозяйстве, то микрометр — дорогой производственный контрольно-измерительным прибор, высокая точность показаний которого в быту не нужна.

Рис. 14 Как измерить диаметр трубы штангенциркулем

Как измерить диаметр трубы при помощи бечевки и по формуле

Иногда решение задачи, как измерять диаметр трубы, затрудняется из-за неудобства проведения замеров, больших габаритных размеров трубопровода — в этих случаях можно использовать комбинированный метод.

Для этого трубу обвязывают нитью или веревкой (можно сделать несколько витков), и ставят на них отметку маркером или ручкой. Затем выкладывают нить на стол и измеряют расстояние между отметками. Полученное значение делят на число пи, равное 3,142, и получают искомый размер. Данный способ, как рассчитать диаметр, позволяет узнавать параметры трубопровода с более высокой точностью благодаря тысячным значениям числа пи и большей протяженности длины окружности, чем напрямую измеренного параметра.

Иногда бывает сложно установить внутренний трубный размер по ряду причин, в этом случае задачу, как определить диаметр трубы, решают комплексным методом. Вначале замеряют ее внешний размер в окружности, затем толщину стенки, после чего по формуле делят первый показатель на число пи и отнимают от него двойную толщину оболочки.

Рис. 15 Как измерить диаметр трубы с использованием лент для замеров и внешний вид циркомера

Измерительными лентами

Один из самых быстрых способов, как замерить диаметр трубы – использовать ленты с размерными шкалами. Иногда для этих целей применяют строительную рулетку, которая имеет гибкую ленту с нанесенными делениями и проставленными значениями длины.

В быту часто встречается сантиметровая лента, которая применяется для определения размеров одежды в шитье, ее также можно использовать аналогично рулетке. После замеров длины по внешнему кругу проводят несложный расчет: результат делят на 3,142 и находят таким способом наружный диаметр.

Аналогом бытовых ленточных измерителей является производственный циркомер – специальный прибор с градуированной гибкой стальной полосой для измерения длин окружностей.

Методом копирования фотосъемки

Фотографический способ позволяет узнавать параметры трубопровода в экстремальных и аварийных условиях при отсутствии освещенности, плохого доступа к коммуникациям, ограниченном временном интервале. При замерах трубных диаметров при помощи фотосъемки рядом с трубой размещают рулетку с делениями или любой предмет, которой можно унести с собой, и делают фотоснимок фотоаппаратом или сотовым телефоном. Затем в спокойных условиях анализируют фотографию, сопоставляя размеры цифровой шкалы рулетки или габаритов предмета с параметрами трубы.

Рис. 16 Сравнительная таблица диаметров водопроводных труб из различных материалов

Благодаря стандартному ряду типовых размеров стальных, медных, полимерных трубопроводов, задача, как узнать диаметр трубы, в большинстве случаев успешно решается изучением соответствующих госстандартов. Если по каким-либо причинам возникает необходимость в замерах, для бытовых целей вполне можно обойтись линейкой, рулеткой, использовать измерительные ленты или кусок бечевки, получив искомый результат при помощи простой формулы.

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат: r2 = x2 + y2

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат: r2 = (x – a)2 + (y – b)2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Круг и окружность

Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.

А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.

Источник