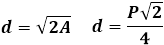как узнать длину диагонали

Диагональ прямоугольника

Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.

Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.

Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.

Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.

Как найти диагональ прямоугольника

Воспользуемся теоремой Пифагора и формулой

d — диагональ квадрата

a — длина прямоугольника

b — ширина прямоугольника

Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.

Диагональ прямоугольника онлайн калькулятор

Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.

Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.

Источник

Геометрические фигуры. Прямоугольник. Формулы.

Диагонали прямоугольника.

Диагонали прямоугольника имеют одинаковую длину.

Диагонали прямоугольника делятся точкой пересечения пополам.

Длина диагонали прямоугольника можно вычислить по теореме Пифагора. И она равняется квадратному корню из суммы квадратов длины и ширины.

Формулы для вычисления длины диагонали прямоугольника:

1. Формула диагонали прямоугольника через 2 стороны прямоугольника (по теореме Пифагора):

2. Формула диагонали прямоугольника через площадь и сторону:

3. Формула диагонали прямоугольника через периметр и сторону:

4. Формула диагонали прямоугольника через радиус окружности (описанной):

5. Формула диагонали прямоугольника через диаметр окружности (описанной):

6. Формула диагонали прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:

7. Формула диагонали прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны, которая прилегает к этому углу:

8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Признаки прямоугольника.

— Если диагонали его имеют одинаковую длину.

— Если квадрат диагонали параллелограмма равняется сумме квадратов смежных сторон.

— Если углы параллелограмма имеют одинаковую величину.

Стороны прямоугольника.

Формулы для определения длин сторон прямоугольника:

1. Формула стороны прямоугольника (длина и ширина прямоугольника) через диагональ и еще одну сторону:

2. Формула стороны прямоугольника (длина и ширина прямоугольника) через площадь и еще одну сторону:

3. Формула стороны прямоугольника (длина и ширина прямоугольника) через периметр и еще одну сторону:

4. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол α:

5. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол β:

Окружность, описанная вокруг прямоугольника.

Формулы определения радиуса окружности описанной вокруг прямоугольника:

1. Формула радиуса окружности, которая описана около прямоугольника через 2-е стороны:

2. Формула радиуса окружности, которая описана около прямоугольника через периметр квадрата и сторону:

3. Формула радиуса окружности, которая описана около прямоугольника через площадь квадрата:

4. Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата:

5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):

6. Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:

7. Формула радиуса окружности, которая описана около прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны у этого угла:

8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Угол между стороной и диагональю прямоугольника.

Формулы для определения угла между стороной и диагональю прямоугольника:

1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

Угол между диагоналями прямоугольника.

Формулы для определения угла меж диагоналей прямоугольника:

1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:

Источник

Как найти диагональ в прямоугольнике

Иногда кажется, что школьные знания нам никогда не пригодятся в реальной жизни. Я тоже так думала: неужели я когда-нибудь буду вспоминать, как найти диагональ в прямоугольнике? Оказалось, да! Я швея, сейчас мастерю прямоугольную подушку для куклы. В качестве декора я захотела пришить к одной из диагоналей тонкую полоску ткани и расшить ее бисером. Для этого мне нужно было точно знать размер этой линии, а сантиметровой ленты под рукой не оказалось. Тогда-то я и стала вспоминать уроки математики.

Вычисление диагонали по сторонам прямоугольника

Зная длину и ширину прямоугольника, можно найти его диагональ. Мне повезло: эти размеры я записала еще на этапе моделирования игрушечного аксессуара.

Если в прямоугольнике провести диагональ, то у нас получится два одинаковых прямоугольных треугольника, в которых диагональ является гипотенузой. Как ее найти, знает каждый школьник и вспомнит любой взрослый: по теореме Пифагора.

Квадрат гипотенузы – это сумма квадратов катетов треугольника.
Соответственно, сама гипотенуза – квадратный корень из этой суммы.

Длина моей заготовки составила 16 см, а ширина – 12 см. С поставленной задачкой я справилась без калькулятора. Как оказалось, корень из суммы квадратов этих чисел идеально извлекается без остатка – записала в ответ 20 см. С этими значениями мне, конечно, повезло случайно. Если бы я решила сделать подушечку с чуть меньшими или большими размерами, такого красивого ответа я бы не получила, и пришлось бы воспользоваться калькулятором.

Определение диагонали по периметру и площади прямоугольника

Есть еще один способ, как найти диагональ в прямоугольнике. Этот метод скорее из математических задач, а не из жизни. Представим, что из условия мы знаем: периметр прямоугольника 56 см и его площадь 192 см^2.

Периметр – это сумма всех сторон прямоугольника.
P = (a + b) * 2
Площадь – это произведение двух сторон.
S = a * b

Подставим значения для периметра и выразим длину:
(a + b) * 2 = 56
a + b = 28
a = 28 – b

Подставим значения для площади и найдем ширину с помощью полученной формулы длины:
a * b = 192
(28 – b) * b = 192
b^2 – 28b + 192 = 0

Подставляем каждый из них в формулу длины:
a = 28 – b

Пожалуй, здесь все просто: поскольку a – это длина, а b – это ширина, очевидно, что длина больше ширины. Поэтому в примере a = 16, b = 12 см.

Мы нашли стороны прямоугольника. А чтобы найти саму диагональ, обращаемся к первому способу, вычисляем через теорему Пифагора и получаем тот же ответ – 20 см.

Конечно, в жизни мы вряд ли будем вспоминать, как найти диагональ в прямоугольнике, потому что можно просто измерить ее линейкой. Но когда инструмента нет под рукой, это знание еще как пригодится.

Источник

Диагональ квадрата

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
— Все стороны квадрата равны (от ромба)
— Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

a 2 +b 2 =c 2
a 2 +b 2 =d 2
2a 2 =d 2

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр

Источник

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

где \( \small a \) и \( \small b \) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем \( \small b \) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

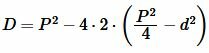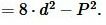(11)

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Источник