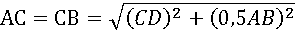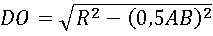как узнать длину дуги зная длину хорды
Определить длину дуги окружности без применения тригонометрических функций.
1. Построим на плоскости из точки 0 радиусом R окружность, для которой произвольный отрезок АВ (АВ 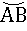
При этом линейные размеры хорды АВ можно измерить обычной линейкой, что никак нельзя применить к дуге. Тогда путем разбиения данной дуги на множество малых и равных прямолинейных отрезков (хорд), а затем, суммируя их, попробуем максимально приблизится к истинному значению длины дуги.
Этот метод использовался еще в древней Греции 2,5 тыс. лет назад когда первые известные нам геометры Антифон и Анаксагор пытались решить задачу о квадратуре круга вписывая в круг правильные многоугольники с большим числом сторон, тем самым стараясь как бы спрямить линию окружности и найти равную ей по длине суммы прямолинейных отрезков, но был в своё время отвергнут наукой по понятным соображениям, но все же, пойдем этим старым и забытым путем,- поделим дугу вначале на две равные части в точке С, получив таким образом две равные дуги и соответствующие им хорды АС и СВ.
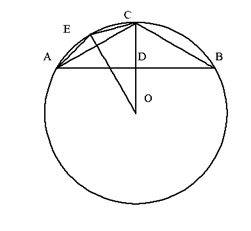
Теорема Пифагора и тривиальные алгебраические преобразования приводят нас к уравнению, известному ещё в Древнем Египте и Греции:
АС=СВ= CD 2 + 0,5 AB 2
CD=R – DO → DO = R 2 — 0,5 AB 2
= 2 R 2 — 2 R R 2 — (0,5 AB ) 2 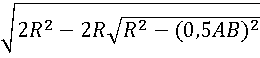
Преобразуя полученную формулу, имеем:
AC = R 2- 4- ( AB R ) 2 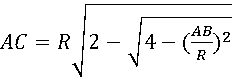
Так как формула (2) была выведена для произвольной хорды, то ее можно применить для нахождения любых других хорд, полученных при последовательном разбиении дуги на все более и более малые отрезки, кратные 1/2 n первоначальной дуги АВ 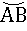
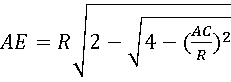
Или, подставив значения предыдущей формулы (2) в (3) получим:
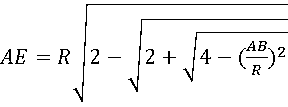
Таким образом, через значения радиуса R и начальной хорды АВ, можно путем разбиений кратное 2 n дуги АВ получить значения соответствующих хорд.
a 2 t n = R 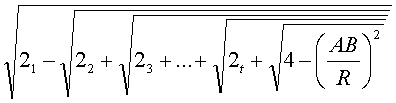
Получая рекуррентным методом последующую формулу из предыдущей, образуется общая формула с чередующими радикалами, число которых зависит от выбранного параметра t.
Метод математической рекурсии, содержащий в своей основе метод математической индукции, позволяет доказать формулу со требуемой математической строгостью. (Доказательство приведено далее.)
Тогда сумма этих отрезков будет тем ближе к значению длины дуги, чем больше число t. Таким образом, длиной дуги будет предел, к которому стремится сумма длин этих прямолинейных отрезков (хорд) при неограниченном возрастании их числа и неограниченном убывании их длины.
Дано: радиус окружности R = 10 (здесь и далее в задачах даны условные единицы), хорда АВ = 3.
Найти : длину дуги 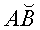
1) Решим задачу с использованием формулы (6):
Проверим правильность решения «классическим» способом с использованием тригонометрических функций:
а) Найдем центральный угол окружности данного радиуса соответствующий хорде АВ:
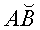
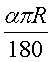
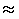
Заметим, что при вычислениях не использовались тригонометрические таблицы, значения углов и даже частица 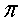
Определить длину хорды окружности без применения тригонометрических функций.
Из формулы (6) посредством простых алгебраических преобразований можно получить такую формулу, которая позволит вычислить хорду а, если известны радиус данной окружности R и длина дуги 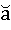
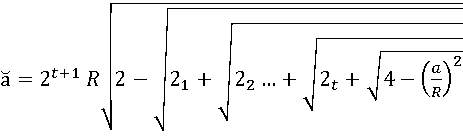
последовательно возводя обе части уравнения в квадрат и перенося из правой части уравнения в левую полученные значения приходим к выражению:
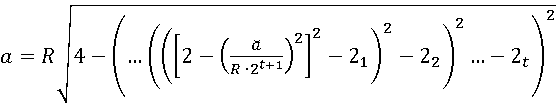
Т.е. зная длину дуги 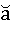
дана окружность с радиусом R =12 и дуга этой окружности а 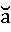
Выбирая параметр формулы t =4, подставляем в формулу (8) известные данные и получаем а≈2,992.
Проверим полученный результат классическим способом:
1. Найдём градусную меру дуги а 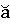
λ = 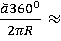
а= 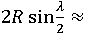
Приведённые выше формулы можно применять для решения различных задач иногда более эффективнее, чем привычными методами.
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Длина дуги окружности — формула, обозначение, примеры расчета
В любой отрасли знаний существует два подхода: академический (теоретический) и прикладной (практический). На стыке этих тенденций всегда находилась геометрия. Определить значение длины дуги окружности и рассчитать площадь круга пытались ещё строители древнеегипетских пирамид. Аналогичные задачи актуальны до сих пор и не потеряют важности для человечества в любую эпоху.
Необходимость расчётов
Геометрическими формулами, связанными с подсчетом площади сектора, объема сегмента и периметра полукруга, следует виртуозно владеть людям, связавшим свою жизнь со строительством или благоустройством территорий. Чтобы обновить после зимы элементы архитектуры городского парка и закрасить дефекты абстрактных скульптур, не нужно вспоминать сложные уравнения, достаточно применить знание геометрических формул.
К примеру, для правильного нахождения веса декоративного камня, предназначенного для окантовки части клумбы, нужно уметь быстро посчитать размер полуокружности на поверхности ландшафта. Затем необходимо определиться с ценой и принять решение, какой камень можно покупать с учетом сметы. Аналогичная задача возникает при строительстве альпийской горки. Тяжесть камня обеспечит круговую укладку, это свойство позволит высадить декоративные растения в запланированных местах сечения, придав конструкции форму трапеции.
Что представляет собой часть клумбы? Это сектор геометрической фигуры. Внешняя его часть — окантовка клумбы — чаще всего представляет собой дугу окружности. Существует две методики вычисления этой величины:
Определение методики расчета в полевых условиях зависит от наличия инструментов и особенностей рельефа местности. Но сначала немного теории. Дугой называют часть окружности, расположенную между двумя произвольными точками, находящимися на ней.
Для удобства рассмотрим пример с двумя точками A и B, расположенными на окружности на небольшом расстоянии друг от друга. Они делят её на 2 части — большую и меньшую. Каждая из них называется дугой окружности.
Градусная мера
Длина дуги между точками окружности является функцией центрального угла, образованного радиусами круга (см. рисунок) в прямо пропорциональной зависимости. На этом основана градусная мера.
За 1° дуги принимают часть окружности.
Определим значение l для угла 120° с радиусом, равным 5 мм: l=3,14*30*5/180=2,62 мм.
Применение хорды и высоты
Существует методика расчета длины дуги по хорде и высоте перпендикуляра. Она получила название формулы Гюйгенса. Хорда представляет собой часть прямой, расположенной внутри окружности. Проходящая через центр хорда называется диаметром.
Формулу Гюйгенса применяют, если центральный угол меньше 60 градусов. Для проведения вычислений необходимо сначала соединить точки окружности прямой линией. Это будет хорда. Далее нужно провести перпендикуляр из ее середины, а из точки соприкосновения перпендикуляра с дугой начертить две прямые линии к концам хорды.
Замерив хорды L и l, можно получить значение дуги, обозначенной на рисунке синим цветом. Если L равна 30 мм, а l — 20 мм, то Р=2*20+3,33=43,33 мм.
Теперь, когда существует понимание методики расчета, можно воспользоваться онлайн-калькулятором. Этот инструмент хорош для проверки полученного экспериментальным путем результата, особенно при обработке большого количества данных, когда необходимо быстро получить ответ.
Онлайн-калькулятор позволяет сохранять полученные значения в буферной памяти компьютера. Оформить данные в виде произвольной таблицы или графика в системе координат не составит труда. Длина дуги окружности по онлайн-калькулятору считается с использованием любой из двух формул: либо по градусной мере, либо по хорде и высоте. Образно говоря, эти формулы являются синонимами, они взаимозаменяемы.
Практика с задачами
Нужно сказать несколько слов об изучении геометрии в средних классах общеобразовательной школы. Существует категория учащихся, для которых формулы сложны для восприятия. Таким ученикам требуется наглядный материал.
На уроке геометрии при изучении материала по вычислениям параметров окружности можно провести практическое занятие. Для этого следует предварительно подготовиться: сделать небольшой чертеж-проекцию гимнастического кольца. Цель занятия — научиться использовать формулы в процессе работы. Ход урока:
Далее следует разделить класс на 4 небольших группы. Каждой из них нужно дать задание по проведению вычислений с использованием изученных формул.
На выполнение задания отводится 12 минут. После истечения времени от каждой из четырех групп выходит ученик, поясняет формулу и записывает на доске полученный результат. Эти ответы сравниваются с уже готовыми замерами, записанными ранее на правой стороне доски.
Следующие 7 минут урока отводятся на обсуждение полученного результата и анализа возникновения погрешности.
Усложнение формулы
Группе продвинутых учеников предлагается задание «Как изменить градусную формулу?». Можно ли найти значение радиуса, используя другие геометрические выражения, например, представить его как половину диаметра круга? В этом случае формулы будет выглядеть следующим образом: r=1/2d, тогда l= πd/360*n.
Обозначаться радиус будет интересно — в виде производной квадратного корня. Вывести формулу нетрудно, это станет прекрасной ментальной гимнастикой для учащихся.
Базовая цель уроков математики — развитие аналитического мышления учащихся достигается в процессе обсуждения и сравнения различных методик расчета. В качестве дополнительного задания можно предложить ученикам посчитать значение кривой линии наружного края школьной клумбы. Затем следует попросить обосновать свои расчеты.
Использование наглядности поможет учащимся подружиться с формулами, увидеть роль геометрии в повседневной практической жизни и облегчить усвоение конкретного материала.