как узнать длину гипотенузы треугольника

Найти гипотенузу треугольника формула

Гипотенуза, что такое гипотенуза. Формула гипотенузы треугольника. Как найти гипотенузу, примеры задач на поиск гипотенузы. Посчитать длину гипотенузы онлайн.

О гипотенузе.

Что такое гипотенуза!?

С самого начала начнем с определение, что такое гипотенуза :

Гипотенуза (греч. ὑποτείνουσα, натянутая) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза существует только у прямоугольного треугольника!

Гипотенузу можно найти по теореме Пифагора

Формула гипотенузы треугольника :

Дадим определение формулы гипотенузы треугольника:

Гипотенуза треугольника равна корню квадратному из квадратов сторон треугольника.

Задача/пример найти длину гипотенузы.

Найдите длину гипотенузы, если длина стороны а = 8см и длина стороны b = 6см.

Нам уже не нужно выводить дополнительные формулы, мы уже это сделали выше:

Нам нужно всего лишь заменить наши буквенные обозначения числовыми значениями.

Корень из 100 равен 10.

Длина гипотенузы в прямоугольном прямоугольнике, у которого одна сторона равна 8 см, а вторая 6см, равна 10

Найти длину гипотенузы онлайн

Для того, чтобы найти длину гипотенузы онлайн, вы можете воспользоваться нашей страницей.

Для того, чтобы найти длину гипотенузы :

В первом поле введите длину первой стороны.

Во втором поле введите длину второй стороны.

Источник

Гипотенуза и угол «α» прямоугольного треугольника

Свойства

Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1) β=90°-α a=c sin⁡α b=c cos⁡α

Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов. P=a+b+c=c sin⁡α+c cos⁡α+c=c(sin⁡α+cos⁡α+1)

Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения. S=ab/2=(sin⁡α cos⁡α)/2

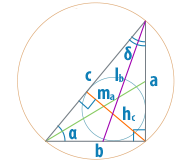
Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2) h=b sin⁡α=c cos⁡α sin⁡α

Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.3) m_с=c/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗⁡α+〖c^2 cos^2〗⁡α )/2=(с√(3 sin^2⁡α+1))/2 m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2⁡α+sin^2⁡α )/2=(с√(3 cos^2⁡α+1))/2

Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.4) l_с=(ab√2)/(a+b)=(c sin⁡α cos⁡α √2)/(sin⁡α+cos⁡α ) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cos⁡α √(2c(c cos⁡α+c) ))/(c cos⁡α+c)=(c cos⁡α √(2(cos⁡α+1) ))/(cos⁡α+1) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sin⁡α √(2c(c sin⁡α+c) ))/(c sin⁡α+c)=(c sin⁡α √(2(sin⁡α+1) ))/(sin⁡α+1)

Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7) M_a=a/2=(c sin⁡α)/2 M_b=b/2=(c cos⁡α)/2 M_c=c/2

Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее. Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два. Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6) r=(a+b-c)/2=(c sin⁡α+c cos⁡α-c)/2=c/2 (sin⁡α+cos⁡α-1) R=c/2

Источник

Гипотенуза прямоугольного треугольника

Гипотенуза прямоугольного треугольника.

Гипотенуза – самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Гипотенуза прямоугольного треугольника (определение и понятие). Что такое гипотенуза?

Рис. 1. Гипотенуза прямоугольного треугольника

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

По катету и гипотенузе или по двум катетам можно судить о равенстве двух прямоугольных треугольников.

Тригонометрические функции, связанные с гипотенузой:

– синус α – отношение катета, противолежащего углу α, к гипотенузе.

Рис. 2. Гипотенуза прямоугольного треугольника

– косинус α – отношение катета, прилежащего углу α, к гипотенузе.

– тангенс α – отношение катета, противолежащего углу α, к катету, прилежащему углу α.

– котангенс α – отношение катета, прилежащего углу α, к катету, противолежащему углу α.

– секанс α – отношение гипотенузы к катету, прилежащему углу α.

– косеканс α – отношение гипотенузы к катету, противолежащему углу α.

Длина гипотенузы прямоугольного треугольника:

Длина гипотенузы прямоугольного треугольника находится с помощью теоремы Пифагора, которая утверждает, что:

Сумма квадратов катетов равна квадрату гипотенузы.

.

Также: α – угол, противолежащий стороне a, β – угол, противолежащий стороне b.

Рис. 3. Гипотенуза прямоугольного треугольника

Длина гипотенузы равна отношению длины катета и косинуса прилежащего угла.

Длина гипотенузы равна отношению длины катета и синуса противолежащего угла.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Справочники

Мировая экономика

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник

Калькулятор прямоугольного треугольника

Корзина

Как пользоваться онлайн-калькулятором. В форме укажите известные параметры прямоугольного треугольника:
а) 2 катета,
б) катет и гипотенуза,
в) катет и противолежащий острый угол,
г) гипотенуза и острый угол.
Заполните поле «Текст с картинки». Нажмите «Решить».

При помощи калькулятора прямоугольного треугольника можно найти гипотенузу онлайн, а также катеты, величины острых и противолежащих углов прямоугольного треугольника.

В форме калькулятора гипотенузы указываются два параметра прямоугольного треугольника онлайн: две стороны или острый угол и сторона.

Для углов имеются два поля: для градусов и для минут.

Далее заполнить поле «Текст с картинки» и нажать «Решить». Компьютерная программа автоматически сделает расчет.

Приводятся ответы с подробными решениями, включая формулы. Для решения задач используется теорема Пифагора. Катеты и гипотенуза вычисляются через синус.

Примеры решения калькулятора прямоугольного треугольника:
1) как найти неизвестный катет или катеты, если известна гипотенуза, равная 2 см, и острый угол 20°. В поле для гипотенузы «c» указывается 2, в поле «Угол (градусов, °)» ставится 20, в поле «Угол (минут, ‘)» указывается 0. Ответ онлайн калькулятора прямоугольного треугольника: длина катетов a = 0,68 см; b = 1,88 см, острый угол B = 70°.

2) пример вычисления неизвестных сторон и острых углов прямоугольного треугольника по двум катетам или по гипотенузе и катету. Вопрос: как найти угол прямоугольного треугольника, зная его стороны, т.е. зная 2 катета или 2 стороны. Известна длина катетов a=11, b=60.

В полях для катетов «a» указывается 11, в поле «b» 60. Нажать «Решить». В ходе решения находим третью сторону – гипотенузу – и находим угол в прямоугольном треугольнике, уже зная все стороны.

Ответ калькулятора гипотенузы: гипотенуза c=61, значения углов A= 10°23′, B = 79°37′. Если даны катет и гипотенуза, то заполняются поля для катета «a» и для гипотенузы «c».

3) с помощью этого онлайн-калькулятора можно решить задачу, где требуется найти катет онлайн, или как найти гипотенузу, зная катет и угол. Например, a=3, противолежащий угол = 30°27′. В поле для катетов «a» указывается 3, в поле «Угол (градусов, °)» ставится 30, в поле «Угол (минут, ‘)» указывается 27. Ответ калькулятора углов прямоугольного треугольника: гипотенуза c = 5,92; катет b = 5,10; угол 59°33’.

Калькулятор сторон прямоугольного треугольника может найти гипотенузу по катету и углу. Онлайн калькулятор гипотенузы находит катет по гипотенузе и углу.

Если стоит задача, как найти катет, если известна гипотенуза и угол, то можно использовать решение прямоугольного треугольника на этой странице. Гипотенузу прямоугольного треугольника, его угол быстро вычисляет компьютерная программа. Калькулятор теоремы Пифагора может найти катет по углу и катету.

Здесь предлагаются ответы на тесты, если требуется вычислить угол по двум катетам. Расчет гипотенузы выполняется онлайн.

Вычисление гипотенузы и углов прямоугольного треугольника при помощи калькулятора катетов дает ответы на следующие тестовые задания по теме «катет и гипотенуза«:
— как найти угол прямоугольного треугольника, зная его стороны,
— узнать гипотенузу, катет прямоугольного треугольника,
— определить гипотенузу по двум катетам,
— рассчитать третью сторону прямоугольного треугольника,
— вычислить катет, если известна гипотенуза и угол,
— найти решение прямоугольного треугольника,
— определить длину гипотенузы, зная 2 катета,
— посчитать угол в прямоугольном треугольнике,
— узнать гипотенузу по катетам,
— рассчитать величину угла в градусах и минутах по катетам,
— найти длину катета по катету и углу,
— вычислить угол или углы прямоугольного треугольника онлайн,
— решить прямоугольный треугольник,
— подсчитать угол по катетам,
— найти сторону прямоугольного треугольника,
— рассчитать прямоугольный треугольник онлайн.

Источник

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

Теорема Пифагора

Сумма квадратов катетов составляет квадрат гипотенузы:

Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.

Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.

Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).

Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:

В тригонометрии

Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.

В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:

sin 2 α + cos 2 α = 1

Гипотенуза прямоугольного треугольника

Связана со сторонами следующими соотношениями (см. рис. 1):

a – противолежащий α катет;

Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.

Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.

Гипотенуза равнобедренного треугольника

В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.

Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.

Пример решения задачи

Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.

AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:

В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.

Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.

Источник