как узнать длину катета

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Источник

Катет прямоугольного треугольника

Катет прямоугольного треугольника.

Катет – одна из двух сторон прямоугольного треугольника, образующих прямой угол.

Катет прямоугольного треугольника (определение и понятие). Что такое катет?

Рис. 1. Катеты прямоугольного треугольника

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

С катетами совпадают две из трёх высоты прямоугольного треугольника.

По катету и гипотенузе или по двум катетам можно судить о равенстве двух прямоугольных треугольников.

Тригонометрические функции, связанные с катетом:

– синус α – отношение катета, противолежащего углу α, к гипотенузе.

Рис. 2. Катеты прямоугольного треугольника

– косинус α – отношение катета, прилежащего углу α, к гипотенузе.

– тангенс α – отношение катета, противолежащего углу α, к катету, прилежащему углу α.

– котангенс α – отношение катета, прилежащего углу α, к катету, противолежащему углу α.

– секанс α – отношение гипотенузы к катету, прилежащему углу α.

– косеканс α – отношение гипотенузы к катету, противолежащему углу α.

Длина катета прямоугольного треугольника:

Длина катета прямоугольного треугольника находится с помощью теоремы Пифагора, которая утверждает, что:

Сумма квадратов катетов равна квадрату гипотенузы.

Также: α – угол, противолежащий стороне a, β – угол, противолежащий стороне b.

Рис. 3. Катеты прямоугольного треугольника

Длина катета равна произведению длины гипотенузы и косинуса прилежащего угла.

Длина катета равна произведению длины гипотенузы и синуса противолежащего угла.

Длина катета равна произведению длины другого катета и тангенса противолежащего угла, относительно искомого катета.

Длина катета равна произведению длины другого катета и котангенса прилежащего угла, относительно искомого катета.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Справочники

Мировая экономика

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник

Понятия и определения

Знак треугольника в первом веке ввёл в обиход древнегреческий философ и учёный Герон. Его свойства изучали Платон и Евклид. По их мнению, вся поверхность прямолинейного вида состоит из множеств различных треугольников. В геометрии под ними понимается область, лежащая в плоскости, ограниченной тремя отрезками, соединяющимися в трёх точках, не принадлежащих одной прямой.

Линии, образующие область, называются сторонами, а точки соприкосновения отрезков — вершинами. Основными элементами многоугольника являются:

В зависимости от видов углов, треугольники разделяют на остроугольные, тупоугольные и прямоугольные. Но каким бы ни был тип фигуры, существует закономерность, что сумма всех углов всегда равна 180 градусам. Поэтому как минимум два угла должны быть острыми.

Различают треугольники и по числу равных сторон. Так, если они все равны, фигура называется равносторонней. Когда же по величине совпадают только две стороны, то многоугольник является равнобедренным. Его главное свойство в том, что углы равны. Частным случаем равнобедренного многоугольника является правильный треугольник (разносторонний).

Свойства прямоугольного треугольника

Прямоугольный треугольник — это симметричный многоугольник, сумма двух углов которого равняется 90 градусов. Так как общая сумма всех трёх углов составляет 180 градусов, то соответственно третий угол равен 90 градусам. Стороны, образующие его, называют катетами, а оставшийся отрезок гипотенузой.

К основным свойствам фигуры относят следующее:

Эти основные признаки при решении геометрических задач помогают определить класс треугольника и рассчитать его величины. Большое значение при этом имеет вычисление значений катетов.

Так, если известна гипотенуза, то найти катеты, зная угол, не составит труда. Определив же длину катетов, вычислить оставшуюся сторону можно по теореме Пифагора. Периметр фигуры определяют сложением двух катетов и гипотенузы, а площадь находят перемножением катетов и делением полученного ответа на два.

Зная катеты, довольно просто вычислить угол. Нужно всего лишь запомнить, что соотношение сторон между собой равно тангенсу противолежащего угла и котангенсу, находящемуся рядом. При этом, зная любой из углов, найти второй можно простым вычитанием известного значения из девяноста. Высота же у прямоугольника равна косинусу прилежащего угла.

Теорема Пифагора и углы

Используя это фундаментальное правило и свойство, что катет, расположенный напротив угла в 30 градусов, равен половине гипотенузы, проводят множество расчётов, связанных с вычислением длин сторон. Для доказательства, что AC = BC/2, приводят следующие рассуждения.

Так как вершина B равна 30 градусам, то, согласно правилу, разворот С должен составлять C =30*2 = 60 градусов. К имеющемуся треугольнику можно приложить точно такую же фигуру, делая сторону AB центром симметрии. Тогда для многоугольника BCD будет справедливо, что B = D = 60º. Исходя из этого можно утверждать, что DC = BC. Но, так как AC = ½ DC, то соответственно AC = ½ BC.

Но не всегда известны все данные, необходимые для нахождения длины катета по приведённым теоремам. Поэтому для вычисления катетов используются и тригонометрические соотношения.

Тригонометрические формулы

Для нахождения длины катета прямоугольного треугольника используют простые формулы. Для их применения нужно знать значение любой из сторон и величину разворота произвольной вершины. Существует четыре способа, позволяющих найти катет с использованием тригонометрических правил:

Зная, как выглядят тригонометрические формулы и содержание двух теорем, вычислить значение катета можно будет в большинстве поставленных задач.

Типовые примеры

Для решения задач на нахождение катета не нужно обладать какими-то особенными знаниями. Нужно просто внимательно проанализировать условие. Например, пусть известно, что в прямоугольнике один катет длиннее другого на пять сантиметров. При этом площадь фигуры равняется 84 сантиметрам в квадрате. Необходимо определить длины сторон и периметр.

Так как в условии дана площадь, то при решении необходимо отталкиваться от неё. Известно, что площадь прямоугольного треугольника находится по формуле: S = AC*CB/2. Это выражение является частным случаем общей формулы для нахождения площади любого треугольника, где: AC — это высота, а CB — основание. Если принять, что AC равно X, то, согласно условию, длина CB будет составлять x+5.

Длина второго катета равняется семи сантиметрам. Первого: AC = 7−5 = 2 см. Зная оба катета, по теореме Пифагора можно найти гипотенузу: c = (22 + 72)½ = (4+49)½ = 531/2 = 7,3 см. Найдя длины всех сторон, можно без усилий найти периметр обыкновенным сложением: P = 2+7+7,3 = 16,3 см. Задача решена.

Довольно интересные, но в то же время простые задачи на нахождение сторон и углов при известной длине гипотенузы и значения разворота одной из вершин. Пусть имеется прямоугольный треугольник, у которого гипотенуза BC равняется пяти сантиметрам, а угол между ней и катетом составляет 60 градусов. Нужно определить все остальные стороны и углы.

Источник

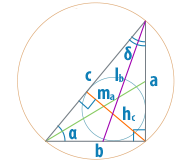
Катеты прямоугольного треугольника

Свойства

В прямоугольном треугольнике, зная катеты, можно найти гипотенузу через теорему Пифагора. Для этого нужно извлечь квадратный корень из суммы квадратов катетов. с=√(a^2+b^2 )

Площадь прямоугольного треугольника равна половине произведения катетов, а периметр – сумме катетов и гипотенузы. S=ab/2 P=a+b+c=a+b+√(a^2+b^2 )

Углы в прямоугольном треугольнике найти, зная катеты, тоже невероятно просто. Отношение одного катета к другому будет тангенсом противоположного угла и котангенсом близлежащего. (рис. 79.1) tan⁡α=a/b cot⁡α=a/b

С другой стороны, зная один из углов, можно найти второй, отняв его из 90 градусов. α=90°-β

Высота у прямоугольного треугольника всего одна, и она относится к любому из катетов как косинус прилежащего к нему угла. (рис. 79.2) cos⁡α=h/b h=b cos⁡α cos⁡β=h/a h=a cos⁡β

Формула медианы в прямоугольном треугольнике преобразуется в отношение гипотенузы к двум или радикала из суммы квадратов катетов к двум, если даны только катеты. (рис. 79.3) m_c=√(2a^2+2b^2-c^2 )/2=√(2c^2-c^2 )/2=√(c^2 )/2=c/2=√(a^2+b^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2 m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4b^2+a^2 )/2

Биссектриса, опущенная на гипотенузу, вычисляется аналогично произвольному треугольнику, с подстановкой радикала вместо гипотенузы. (рис.79.4) l_c=√(ab(a+b+c)(a+b-c))/(a+b)=√(ab((a+b)^2-с^2))/(a+b)=√(ab(a^2+2ab+b^2-a^2-b^2))/(a+b)=√(ab*2ab)/(a+b)=(ab√2)/(a+b) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b-c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)

Средние линии прямоугольного треугольника образуют внутри него еще один прямоугольный треугольник. Внутренний треугольник будет подобен внешнему, так как средние линии параллельны катетам и гипотенузе, и равны соответственно их половинам. Поскольку гипотенуза неизвестна, для нахождения средней линии M_c нужно подставить радикал из теоремы Пифагора. (рис.79.7) M_a=a/2 M_b=b/2 M_c=c/2=√(a^2+b^2 )/2

Радиус вписанной окружности в прямоугольном треугольнике вычисляется по упрощенной формуле для произвольного треугольника, а радиус описанной окружности является половиной гипотенузы и совпадает с медианой. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+b-√(a^2+b^2 ))/2 R=m=c/2=√(a^2+b^2 )/2

Источник

Катет «A» и угол «α» прямоугольного треугольника

Свойства

Зная один из катетов в прямоугольном треугольнике, можно найти второй катет и гипотенузу используя тригонометрические отношения – синус и тангенс известного угла. Так как отношение противолежащего углу катета к гипотенузе равно синусу этого угла, следовательно, чтобы найти гипотенузу нужно катет разделить на синус угла. a/c=sin⁡α c=a/sin⁡α

Второй катет можно найти из тангенса известного угла, как отношение известного катета к тангенсу. a/b=tan⁡α b=a/tan⁡α

Чтобы вычислить неизвестный угол в прямоугольном треугольнике нужно из 90 градусов вычесть величину угла α. β=90°-α

Периметр и площадь прямоугольного треугольника через катет и противолежащий ему угол можно выразить, подставив полученные ранее выражения для второго катета и гипотенузы в формулы. P=a+b+c=a+a/tan⁡α +a/sin⁡α =a tan⁡α sin⁡α+a sin⁡α+a tan⁡α S=ab/2=a^2/(2 tan⁡α )

Вычислить высоту также можно через тригонометрические отношения, но уже во внутреннем прямоугольном треугольнике со стороной a, который она образует. Для этого нужно сторону a, как гипотенузу такого треугольника умножить на синус угла β или косинус α, так как согласно тригонометрическим тождествам они равнозначны. (рис. 79.2) h=a cos⁡α

Медиана гипотенузы равна половине гипотенузы или известному катету a, деленному на два синуса α. Чтобы найти медианы катетов, приведем формулы к соответствующему виду для известной стороны и углы. (рис.79.3) m_с=c/2=a/(2 sin⁡α ) m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4a^2+a^2/tan^2⁡α )/2=(a√(4 tan^2⁡α+1))/(2 tan⁡α ) m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4b^2+a^2 )/2=√(4b^2+c^2-b^2 )/2=√(3 a^2/tan^2⁡α +a^2/sin^2⁡α )/2=√((3a^2 sin^2⁡α+a^2 tan^2⁡α)/(tan^2⁡α sin^2⁡α ))/2=(a√(3 sin^2⁡α+tan^2⁡α ))/(2 tan⁡α sin⁡α )

Так как биссектрисой прямого угла в треугольнике является произведение двух сторон и корня из двух, деленное на сумму этих сторон, то заменив один из катетов на отношение известного катета к тангенсу, получаем следующее выражение. Аналогично, подставив отношение во вторую и третью формулы, можно вычислить биссектрисы углов α и β. (рис.79.4) l_с=(a a/tan⁡α √2)/(a+a/tan⁡α )=(a^2 √2)/(a tan⁡α+a)=(a√2)/(tan⁡α+1) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(a/tan⁡α √(2c(a/tan⁡α +c) ))/(a/tan⁡α +c)=(a√(2c(a/tan⁡α +c) ))/(a+c tan⁡α ) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(a√(2c(a+a/sin⁡α ) ))/(a+a/sin⁡α )=(a sin⁡α √(2c(a+a/sin⁡α ) ))/(a sin⁡α+a)

Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tan⁡α ) M_c=c/2=a/(2 sin⁡α )

Источник