как узнать длину окружности калькулятор

Онлайн калькулятор. Длина окружности. Периметр круга.

Используя этот онлайн калькулятор, вы сможете найти длину окружности.

Воспользовавшись онлайн калькулятором для вычисления длины окружности (периметра круга), вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти длину окружности

Выберите известную величину

Ввод данных в калькулятор для вычисления периметрa окружности

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины.

Теория. Длина окружности

Формулы для вычисления длины окружности.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Калькулятор длины окружности

Скачать, сохранить результат

Выберите способ сохранения

Информация

Длина окружности находится очень просто, но, тем не менее, это является основой геометрии и изучается еще средней школе. Формула длины окружности имеет следующий вид:

P=2πr,

где P – длина окружности;

π – константа, которая всегда равна 3,14;

r – радиус окружности, длину которой необходимо найти.

Однако, существует еще одна формула и наш калькулятор длины окружности также её использует. Данная формула имеет следующий вид:

P=πd, где

P – длина окружности;

π– константа, которая всегда ровна 3,14;

d – диаметр окружности, длину которой необходимо найти.

Разница между формулами в том, что в первой длина окружности находится через радиус, который умножается на два, а во второй используется сразу диаметр.

Данные формулы применяются в многих сферах жизни человека. От производства каких-либо товаров, до строительства небоскребов. Лица, ответственные за проектирование зданий несут огромную ответственность за верность их расчетов, которые буквально влияют на человеческие жизни и их сохранность. Для того, чтобы избежать человеческого фактора в процессе расчета точных показателей, был создан онлайн калькулятор, в котором легко находится длина окружности через радиус или диаметр.

Благодаря данному инструменту Вы сможете не только получить информацию о том, как найти длину окружности, но и рассчитать её без каких-либо усилий. Калькулятор гарантирует предельную точность расчетов и Вам не нужно задаваться как узнать верны ли расчеты. На сайте показаны формулы, по которым считает калькулятор и это подтверждает то, что любой расчет будет верным.

Источник

Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.

Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.

Длина окружности всегда равна числу π (Пи)

Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…

Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.

Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».

Иными словами Пи ≈ 3,14 диаметрам круга или окружности.

Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна

P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр

Источник

Длина окружности.

Как найти длину окружности? Найдите длину окружности по радиусу или диаметру заполнив поля в калькуляторе ниже.

Длина окружности равна 2ПиR

1. Сложнее найти длину окружности через диаметр, по этому сначала разберём этот вариант.

Пример: Найдите длину окружности диаметр которой равен 6 см. Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.

После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.

2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см

Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.

Онлайн калькулятор длины окружности

Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.

Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.

Источник

Конвертер величин

Длина окружности и площадь круга

Этот калькулятор определяет длину окружности и площадь круга по известным радиусу или диаметру окружности.

Для расчета введите одну из величин: радиус, диметр, площадь или длину окружности и нажмите на кнопку Рассчитать для расчета остальных величин.

Определения и формулы

В геометрии окружностью называется совокупность точек на плоскости, которые находятся на одном расстоянии от точки, называемой центром окружности. Иными словами, окружность — это геометрическое место точек, находящихся в одной плоскости и равноудаленных от точки, называемой центром. Расстояние между любой точкой окружности до центра этой окружности называется радиусом. Мы привыкли видеть окружность в форме круглой линии или круга. Однако так окружность выглядит только в евклидовой геометрии. В некоторых метрических пространствах, например, в чебышевском или манхэттенском пространстве окружности выглядят скорее квадратными.

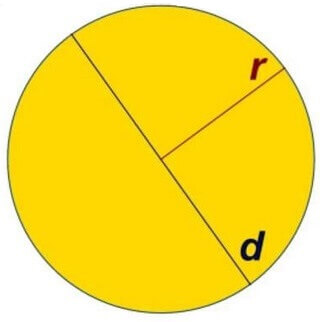
Диаметр круга — это наибольший отрезок, соединяющий две точки на окружности. Или, точнее, это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен ее удвоенному радиусу. Любой диаметр разделяет окружность, а точнее, круг, на две равные половины.

Говоря точным языком, окружность — это линия или замкнутая кривая, которая окружает часть плоскости, называемую кругом.

Длина окружности

Длина C окружности — это длина замкнутой плоской кривой, ограничивающей круг, то есть это расстояние, равное длине границы круга. Она измеряется в единицах длины. Если разделить длину любой окружности на ее диаметр D, получится число 3.14159265359… Это число — одна из самых важных констант в математике, которое обозначается греческой буквой пи ( π ):

где R — радиус окружности. Если решить это уравнение для длины окружности, мы получим формулу, которая всем нам знакома с детства:

Математическая константа π широко используется в многих формулах в математике, технике, архитектуре и строительстве. Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.

Площадь круга

Поскольку TranslatorsCafe.com — сайт для переводчиков, в том числе с английского языка, вначале отметим, что в английском языке площадь круга не совсем корректно называется area of a circle, что буквально означает «площадь окружности», то есть площадь кривой линии (окружность — это кривая!), а, как известно, у линии не может быть площади. Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности.

Итак, площадь A круга, то есть части плоскости, лежащей внутри окружности радиуса R, равна произведению числа π на квадрат радиуса:

Во многих других языках, в том числе и в русском, такой путаницы в терминах «круг» и «окружность» нет. Впрочем, она есть в других терминах. Площадь круга можно также описать как число единичных квадратов, которые покрывают круг, лежащий внутри окружности.

Окружности в архитектуре

Окружность — весьма совершенная форма, потому что каждая точка окружности находится на одном и том же расстоянии от ее центра. Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.

Архитекторы считают окружность и сферу самыми совершенными из всех геометрических форм. Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.

Окружность в технике

Невозможно представить себе технику без колес и других деталей в форме окружности. Некоторые из них (например, шасси самолетов и колеса автомобилей) хорошо видны. Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.

Окружности в сельском хозяйстве

Пролетая над пустынями, в которых ничего не растет, мы часто видим зеленые круги. Это поля, которые имеют такую форму из-за того, что фермеры используют системы кругового орошения с центральной осью, вокруг которой вращается оросительное устройство.

Вас могут заинтересовать и другие калькуляторы из группы «Популярные калькуляторы»:

Популярные калькуляторы

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Источник