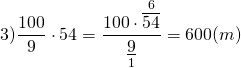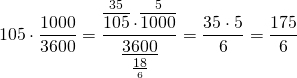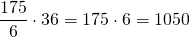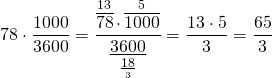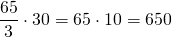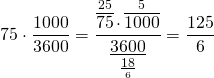как узнать длину поезда по скорости и времени
Текстовые задачи на нахождение длины поезда.
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1. 26+4=30(км/ч) — скорость сближения поезда и пешехода, так как они движутся в разных направлениях.
2. 90/3600=1/40(ч) — время, за которое поезд проезжает мимо пешехода.
3. 30/40=0,75(км) — длина поезда в километрах.
4. 0,75·1000=750(м) — длина поезда в метрах.
Ответ: длина поезда 750 метров.
Поезд, двигаясь равномерно со скоростью 62 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 2 км/ч, за 33 секунды. Найдите длину поезда в метрах.
Решение:
1. 62-2=60(км/ч) — скорость сближения, так как пешеход и поезд движутся в одном направлении.
2. 33/3600=11/1200(ч) — время, за которое поезд проезжает мимо пешехода.
3. 60·11/1200=11/20(км) — длина поезда в километрах.
4. 11/20·1000=50·11=550(м) — длина поезда в метрах
Ответ: длина поезда 550 метров.
Задачи для самостоятельного решения:
1. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 8 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах.
Поезд проезжает мимо пешехода
Рассмотрим задачи, в которых поезд, двигаясь равномерно, проезжает мимо пешехода, движущегося параллельно путям. Известны скорость пешехода, скорость поезда и время проезда поезда мимо пешехода.Требуется найти длину поезда.
Длина поезда равна расстоянию между началом первого вагона и концом последнего вагона. Чтобы найти это расстояние, надо скорость умножить на время (формула пути). Время дано в условии, следовательно, задача сводится к нахождению скорости сближения поезда и пешехода (то есть скорости поезда относительно пешехода).
Если пешеход идёт навстречу поезду, скорость сближения равна сумме скоростей поезда и пешехода.
В случае движения поезда вдогонку пешеходу скорость сближения равна разности скоростей поезда и пешехода.
Поезд, двигаясь со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 54 секунды. Найти длину поезда в метрах.
1)36+4=40 (км/ч) скорость сближения поезда и пешехода
2) Переведём скорость из км/ч в м/с:
(Из неправильной дроби не следует выделять целую часть, поскольку на следующем шаге, при умножении на натуральное число, она будет нужна нам именно в таком виде).
Следовательно, длина поезда равна 600 м.
Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 5 км/ч, за 42 секунды. Найти длину поезда в метрах.
1) 65-5=60 (км/ч) скорость сближения пешехода и поезда.
2) Переводим километры в час в метры в секунду:
Найдите длину поезда
Найдите длину поезда в метрах, если два поезда идут навстречу друг другу либо один поезд догоняет другой (или пешеход идёт навстречу поезду, или пешеход идёт в том же направлении, что и поезд) — один из видов задач из ОГЭ и ЕГЭ.
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского, равно 36 секундам. Ответ дайте в метрах.
При движении навстречу друг другу скорость сближения поездов равна сумме их скоростей:
65+40=105 (км/ч) скорость сближения поездов
Скорый поезд прошел мимо пассажирского за 36 секунд. Умножим скорость сближения поездов на это время:
Длина поезда равна расстоянию от головы поезда до конца последнего вагона. 36 секунд — это время с момента, когда головной вагон скорого поезда поравнялся с головным вагоном пассажирского поезда, до момента, когда последний вагон скорого поезда проехал мимо последнего вагона пассажирского поезда.
Таким образом, 1050 м — это расстояние, между головным вагоном скорого поезда, и головным вагоном пассажирского поезда, то есть 1050 м — это сумма длин двух поездов.
Чтобы найти длину скорого поезда, из суммы длин вычитаем длину пассажирского поезда:
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина товарного поезда равна 1000 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 2 минутам 18 секундам. Ответ дайте в метрах.
Поезда движутся в одном направлении, значит, это движение вдогонку. При движении вдогонку скорость сближения поездов равна их разности:
60-30=30(км/ч) скорость сближения поездов.
Скорый поезд прошёл мимо товарного на 2 минуты 18 секунд. Выразим время в секундах:
2 минуты 18 секунд =2·60+18=138 секунд.
Умножим скорость сближения поездов на это время:
2 минуты 18 секунд — это время с момента, когда головной вагон пассажирского поезда поравнялся с последним вагоном товарного до момента, когда последний вагон пассажирского прошёл мимо головного вагона товарного. То есть расстояние 1150 метров равно сумме длин двух поездов.
Остаётся из суммы длин двух поездов вычесть длину товарного:
1150-1000=150(м) длина пассажирского поезда.
Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 3 км/ч навстречу поезду, за 30 секунд. Найдите длину поезда в метрах.
Так как пешеход идёт навстречу поезду, скорость сближения поезда и пешехода равна сумме их скоростей:
75+3=78 (км/ч) скорость сближения поезда и пешехода.
Скорость из км/ч переведём в м/с: 78 км/ч=65/3 м/с
Умножим скорость сближения поезда и пешехода на время, за которое поезд проезжает мимо пешехода:
650 м — длина поезда.
Поезд, двигаясь со скоростью 79 км/ч, проходит мимо идущего параллельно путям в том же направлении пешехода за 12 секунд. Определите длину поезда в метрах, если скорость пешехода равна 4 км/ч.
Так как поезд и пешеход движутся в одном направлении (движение вдогонку), то скорость их сближения равна разности скоростей:
79-4=75 (км/ч) скорость сближения поезда и пешехода.
Переводим скорость из км/ч в м/с: 75 км/ч=125/6 м/с
Умножим скорость сближения поезда и пешехода на время, за которое поезд проезжает мимо пешехода:
Задачи на движение протяженных тел и сложение скоростей
Это один из самых интересных типов текстовых задач на ЕГЭ по математике. Здесь и задачи на движение протяженных тел. И задачи, где два поезда движутся навстречу друг другу (по параллельным путям, конечно). И такие, где один поезд обгоняет другой.
Расскажем о секретах решения таких задач.
Что значит «движение протяженных тел»?
Если в условии задачи поезд проходит расстояние от Санкт-Петербурга до Москвы — длиной самого поезда можно пренебречь. Она намного меньше расстояния между городами. В физике говорят, что поезд в этом случае можно считать материальной точкой. Если же в задаче один поезд проходит мимо другого или поезд проходит через туннель — длину поезда также надо учитывать.
1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.
Переведем 36 секунды в часы.
За это время поезд проехал
Задачи на встречное движение или обгон удобно решать в движущейся системе отсчета.
2. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина пассажирского поезда равна 400 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 38 секундам. Ответ дайте в метрах.
Решим задачу в системе отсчета, связанную с головой пассажирского поезда. Представим, что мы находимся в кабине машиниста неподвижного поезда, а мимо нас проносится скорый поезд. Скорость, с которой один поезд движется относительно другого, равна
Переведем 38 секунд в часы:
За это время поезд проехал
3. Два поезда движутся навстречу друг другу со скоростями 56 и 52 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 15 секунд. Найдите длину второго поезда. Ответ выразите в метрах.
Если пассажир находится в первом поезде, то в его системе отсчета второй поезд движется навстречу со скоростью, равной сумме скоростей поездов. Иначе она называется «скорость сближения», и она равна
Переведем эту скорость в метры/минуту.
Мы получили, что со скоростью 1800м/мин мимо пассажира первого поезда проходит весь второй поезд. По условию, это происходит за
Длина второго поезда равна
4. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 140 метров, второй — длиной 60 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 800 метров. Через 15 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 1000 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Переведем минуты в часы:
Пусть и — скорости первого и второго сухогрузов. Будем решать задачу в системе отсчета, связанной с первым сухогрузом. Представьте, что вы находитесь на нем и видите, как второй сухогруз догоняет и обгоняет ваш корабль со скоростью
Расстояние, пройденное вторым сухогрузом, — это сумма расстояний от носа второго сухогруза до кормы первого, длины первого сухогруза, расстояния от его носа первого до кормы второго и длины второго (см. рисунок).
На 8 километров в час скорость второго сухогруза больше скорости первого.
Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.