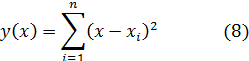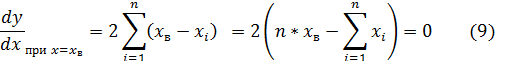как узнать истинное значение измеряемой величины

25.06.202326.06.2023 admin 0 Comments

Истинное значение измеряемой величины

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Приборостроительный факультет

Кафедра экспериментальной и теоретической физики

ИЗУЧЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Методическое указание к лабораторной работе №1

По дисциплине «Общая физика»

Раздел «Механика. Молекулярная физика»

Минск 2011 г.

Введение

I Физические измерения и погрешности

Прежде всего, поясним, что вообще понимается под измерением. Измерением называется сравнение интересующей нас физической величины с соответствующим эталоном или измерительным прибором, проградуированным по эталону. По характеру проведения измерений их делят на прямые и косвенные. Под прямыми измерениями понимают такие измерения, при котором в ходе опыта непосредственно измеряется интересующая нас величина. Однако далеко не все величины можно определить путем прямого измерения. Например, плотность тела, определить непосредственным измерением весьма затруднительно. Но известно, что известно, что плотность определяется по формуле

(1)

Погрешности измерений

Опыты показывают, что истинное значение любой физической величины определить невозможно, т.к. операции измерений производятся приборами, обладающими определенной предельной точностью, а сами измерения сопровождаются целым рядом объективных и субъективных ошибок или погрешностей. По характеру проявления погрешности можно условно разделить на следующие классы: приборные, систематические, случайные.

Приборные погрешности. Если измерительный прибор исправен и отрегулирован, то на нем можно провести измерения с ограниченной точностью, определяемой типом прибора. Принято приборную погрешность стрелочного прибора считать равной половине наименьшего деления его шкалы. В приборах с цифровым отсчетом приборную ошибку приравнивают к величине одного наименьшего разряда шкалы прибора.

При проведении измерений важен не только учет систематических ошибок, но необходимо также добиваться их исключения.

Систематические погрешности условно разделяются на четыре группы:

1) погрешности, природа которых известна и их величина может быть достаточно точно определена. Такой ошибкой является, например, изменение измеряемой массы в воздухе, которая зависит от температуры, влажности, давления воздуха и т.д.;

2) погрешности, природа которых известна, но неизвестна сама величина погрешности. К таким погрешностям относятся ошибки, обусловленные измерительным прибором: неисправность самого прибора, несоответствие шкалы нулевому значению, классу точности данного прибора;

3) погрешности, о существовании которых можно не подозревать, но величина их зачастую может быть значительной. Такие ошибки возникают чаще всего при сложных измерениях. Простым примером такой ошибки является измерение плотности некоторого образца, содержащего внутри полости;

Истинное значение измеряемой величины

Приведенные выше данные показывают, что, строго говоря, измерения истинного значения любой величины невозможно в принципе. Поэтому более корректный способ представления результата любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины, а также интервал, в котором, как он уверен, она лежит. Таким образом, задача экспериментатора состоит в том, чтобы уменьшить влияние погрешностей за счет правильной техники измерений, сделать правильную наилучшую оценку результата измерения и величины погрешности этого результата.

Рассмотрим случай, когда систематические ошибки отсутствуют, а имеют место лишь случайные погрешности. Предположим, что нами произведено n измерений некоторой величины х, при этом получены n значений этой величины х₁ х₂ х_i….х_n. Округлим эти величины с учетом приборной ошибки и расположим в порядке возрастания. Определим в полученном множестве значений количество повторов (выпадений) отдельных результатов – ∆n_i и вычислим вероятности их выпадения по формуле:

(2)

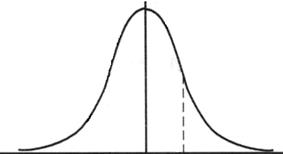
Полученные результаты также внесем в таблицу и построим на их основе график (рис.1) зависимости вероятности повторов отдельных результатов измерения от их величины – х_i, т.е. функцию .

P_max

х_i

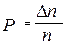
Из полученного рис.1 видно, что наиболее вероятным является некоторый результат х_i= х_в, которому соответствует максимальное значение вероятности выпадения P_max.

Если этот результат (х_в) принять за истинный (Хв = Хи), то абсолютную ошибку каждого измерения ∆х_i, можно найти из выражения: ∆х_i= х_i,– х_в и более того истинный результат измерения, очевидно, должен удовлетворять условию:

В этом можно убедиться, рассчитав абсолютные ошибки всех измерений, числа повторов каждой ошибки ∆n₀ и вероятности выпадения ошибок

Кроме того, как следует из работ немецкого математика Г. Гаусса, все обсуждаемые выше закономерности наблюдаются на рис 2.

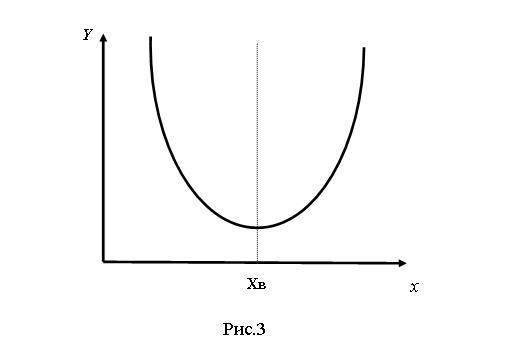
Для повышения точности и снижения трудоемкости Гаусс предложил для нахождения истинного значения измеряемой величины использовать квадратичную функциональную зависимость вероятности ошибок в виде (4) изображенную на рис.3.

(4)

Известно, что для нахождения экстремума функции необходимо приравнять нулю ее производную. Используем для этого новую функцию (4):

Возьмем производную от этой функции и приравняем её нулю.

(5)

После несложных преобразований получаем:

(6)

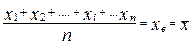
Таким образом, наиболее вероятным значением измеряемой величины является среднее арифметическое , получаемое от нескольких идентичных измерений. И этот же результат соответствует истинному значению многих измерений, представленных на Рис. 1.

Источник

Метрология

Измеряемые величины, виды и области измерений

Основные метрологические понятия

Основными проблемами, которыми занимается метрология, являются:

Понятие о размере

Различают следующие основные понятия размера:

Истинным значением размера называется значение размера, свободное от погрешностей измерений. Истинное значение размера неизвестно и его нельзя определить, так как все средства измерений имеют погрешности, некоторые из которых нельзя учесть и компенсировать.

Погрешностью (ошибкой) измерения называется разность между полученным при измерении значением размера и его истинным значением. Так как истинное значение измеряемой величины неизвестно, то оно заменяется ее точным или действительным значением.
Погрешность прибора может быть также выражена в долях или процентах значения измеряемой величины. В этом случае она называется относительной погрешностью.

Меры и измерительные приборы всегда имеют погрешности, которые изменяются с течением времени в результате износа или старения измерительных средств. Поэтому меры и приборы должны периодически калиброваться.

Калибровкой (сличением) называется процесс определения действительного отклонений показаний прибора или инструмента от заданного значения и соответствия мер и измерительных приборов техническим требованиям.
Калибровка производится посредством образцовых измерительных приборов или мер. Результаты калибровки могут быть использованы для компенсации систематических погрешностей приборов и инструментов.
Калибровку производят изготовители приборов и инструментов, лаборатории, производственные предприятия. Компенсация систематических погрешностей широко применяется при калибровке электронных (индуктивных, инкрементных) измерительных приборов.

Измеряемые величины

Измерения физических величин подразделяются на следующие области и виды:

1. Измерения геометрических величин:

2. Измерения механических величин:

3. Измерения параметров потока, расхода, уровня, объема веществ:

4. Измерения давлений, вакуумные измерения:

5. Физико-химические измерения:

6. Теплофизические и температурные измерения:

7. Измерения времени и частоты:

8. Измерения электрических и магнитных величин на постоянном и переменном токе:

9. Радиоэлектронные измерения:

10. Измерения акустических величин:

11. Оптические и оптико-физические измерения:

12. Измерения ионизирующих излучений и ядерных констант:

Источник

Определение истинного значения измеряемой физической величины и погрешности измерений

Министерство образования и культуры

Республики Кыргызстан

Кыргызский Технический Университет

Методическое руководство

К лабораторным работам по физике.

Раздел «Механика»

Бишкек 2008

Утверждено: Одобрено:

На заседании кафедры Методической комиссией

общей физики энергетического факультета

Составители:

Настоящее руководство к лабораторным работам по механике, составлено в соответствии с программой по физике для высших технических учебных заведений. Её цель – оказать помощь студентам в понимании изучаемого теоретического материала и в работе с различными физическими приборами, а также ознакомить их с элементами проведения физического эксперимента.

В руководстве кратко даются теория, описание установки, методика проведения эксперимента для каждой лабораторной работы.

Вводное занятие

Обработка результатов исследования физического эксперимента.

Цель работы: Изучить элементарные оценки погрешностей измерений физических величин, полученных из эксперимента. Научиться корректно обрабатывать экспериментальные данные лабораторных работах, оформлять результаты эксперимента

Теоретическое введение

Классификация погрешностей измерений.

Результаты любых измерений всегда содержат ошибки различного происхождения, поэтому невозможно измерить абсолютно точно ту или иную физическую величину, как бы тщательно не проводились эксперименты по измерению. На практике (опыте, эксперименте) получают не истинное значение физической величины, а лишь её приближенное значение. В связи с этим на практике важно получить более точный результат, причем, чем точнее результат, тем выше качество измерения, а следовательно, выше качество проделанной работы. Последнее позволяет наиболее достоверно сделать выводы об изучаемом явлении (объекте).

Измерение – это нахождение численного значения физической величины (время, масса, сила, длина и т.д.) опытным путем, с помощью специальных технических средств (весов, штангенциркуля, секундомера и т.п.) и приспособлений.

Под физической величиной следует понимать характеристику одного из свойств физического объекта, поддающаяся количественной оценке и используемая для описаний явлений природы с помощью математических формул.

Измеряемая физическая величина –Х, найденная опытным путем должна иметь числовое значение и размерность, т.е. единицу измерения [В]. С учетом сказанного в общем виде можно записать:

, (1)

Например: длина l =25 м.

Точность и погрешность измерения физической величины определяется различными видами ошибок, а именно: систематическими, случайными, промахами и ошибками приборов.

Систематические погрешности

Случайные погрешности.

Случайные погрешности – это ошибки, связанные с индивидуальными особенностями исследователя, а так же с малозаметными изменениями окружающих условий во время опыта. Например: при изменении напряжения в сети (220В) возможны случайные колебания напряжения, связанные с различными причинами (подключение обогревательного устройства в соседнем помещении, коротком замыкании и др.). Каждая из таких причин сама по себе создает заметное отклонение вольтметра, а суммарное воздействие ряда причин может дать ощутимые отклонения измеряемой величины. Случайные ошибки не поддаются учету. Для того чтобы оценить случайные ошибки, создан математический аппарат, называемый теорией погрешностей измерений, которая базируется на математическом аппарате теории вероятности.

Промахи.

Под промахом понимается грубая ошибка, сделанная в результате неожиданных резких нарушений условий, в которых проводится эксперимент, либо ошибки, связанные с невнимательностью исследователя. Промахи так же относятся к случайным погрешностям.

Например: исследователь снял с прибора одно показание физической величины, а записал другое, или сделал ошибку при переписывании результатов. Наличие промахов оказывает сильное влияние на результаты измерений и поэтому их необходимо исключать. Повторение эксперимента в несколько отличных условиях в большинстве случаев позволит освободиться от промахов, но не дает 100% гарантии.

Погрешности приборов.

Показания любого прибора, даже самого точного и совершенного всегда отличаются от фактического (истинного) значения измеряемой величины. Любой измерительный прибор имеет свою собственную предельную точность, которая определяется его конструкцией и качеством изготовления. Как правило, предельная погрешность прибора указывается в описании прибора или паспорте эксплуатации. Погрешность прибора указывается и на самом приборе, в виде цены деления прибора, так называемая постоянная прибора.

Для характеристики качества прибора вводят понятия чувствительности прибора и цены деления. Под чувствительностью прибора понимают величину, равную числу деления шкалы, на которое перемещается указатель при изменении измеряемой величины на единицу. Например: если нагрузка на чашке весов составляет 1мг, которая вызывает перемещение стрелки на 10 делении, то чувствительность данных весов определяется соотношением:

Цена деления прибора является обратной величиной к чувствительности прибора.

Зная цену деления прибора, можно определить погрешность прибора. Для большинства приборов погрешность принимается равной половине цены наименьшего деления шкалы. Например: при измерении длины обычной школьной линейкой предельная погрешность составит 0,5мм. Погрешность приборов определяется классом точности, который обычно указывается в кружочке на шкале (или корпусе) прибора.

Определение истинного значения измеряемой физической величины и погрешности измерений

Опыт показывает, что при любых экспериментальных исследованиях невозможно найти истинное значение физической величины, а можно лишь получить наилучшую приближенную оценку истинного значения измеряемой величины.

Теория погрешностей дает возможность оценить истинное значение измеряемой величины следующим образом. Пусть в результате измерений получен ряд значений некоторой физической величины –Х₁, Х₂, Х₃,,Х_i…, Х_N., где i=1,N; причем .

В теории погрешности доказывается, что наиболее достоверной приближенной оценкой истинного значения измеряемой величины «а» является среднее арифметическое, определяемое по формуле:

, (2)

В теории погрешностей вводят понятие абсолютной погрешности отдельного измерения, которое обозначается величиной DX_i_.

Абсолютной погрешностью отдельного измерения называют величину DX_i, равную разности между значением i-го измерения и средним значением X_ср, взятым по модулю. Аналитически можно записать так:

(3)

Средней абсолютной погрешностью измерения называется среднее арифметическое абсолютных погрешностей отдельных измерений, которое определяется соотношением:

(4)

Величина DX_ср указывает границы, в которых заключено точное значение искомой физической величины или так называемый доверительный интервал погрешности измерений.

Абсолютная погрешность DX_ср хотя и характеризует качество измерений, но не является исчерпывающей характеристикой. Для оценки точности измерений в теории погрешностей вводится понятие об относительной погрешности измерений.

Относительной погрешностью измерений называют отношение абсолютной погрешности к среднему значению измеряемой величины, выраженной в процентах, которая определяется по формуле:

(5)

Рассмотрим пример. Пусть в результате измерения некоторой физической величин X получены следующие экспериментальные значения, которые занесены в таблицу 1., где N число измерений.

N	1	2	3	4	5	6	7
Х	5,2	5,7	5,5	5,0	4,8	5,3	5,2

По формуле (3) найдем абсолютные погрешности отдельных измерений для данных значений, тогда получим:

аналогично получим для всех семи измерений

С учетом найденных DХ можно определить среднюю абсолютную погрешность результата измерения по формуле (4).

Из последнего следует, что истинное значение измеряемой величины «а» лежит в пределах от Х_ср –DХ_ср до Х_ср+DХ_ср или можно записать так называемый доверительный интервал

Источник

Истинное значение измеряемой величины

Приведенные выше данные показывают, что, строго говоря, измерения абсолютно точно истинного значения любой величины невозможно в принципе. Поэтому более корректный способ представления результата любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины, а также интервал, в котором, как он уверен, она лежит. Таким образом, задача экспериментатора состоит в том, чтобы уменьшить влияние погрешностей за счет правильной техники измерений, сделать правильную наилучшую оценку результата измерения и величины погрешности этого результата.

(6)

P_max

х_i

Если этот результат (х_в) принять за истинный, то абсолютную ошибку каждого измерения ∆х_i, можно найти из выражения: ∆х_i= х_i— х_в и более того истинный результат измерения, очевидно, должен удовлетворять условию:

Затем построим зависимость вероятности выпадения результатов измерений P от (х_i-z) для трех значений z ( z x_в). На рисунке 2 представлена эта зависимость, которая представляет собой туже зависимость P, что на рис.1. ( и получена из тех же результатов ), но сдвинутая на величину z влево по оси абсцисс. Ясно, что P имеет максимум при z=x_в в нуле, а при других значениях z максимум отличается от нуля.

где x_i – результат i-го измерения, n – число измерений, то о её свойствах можно сказать следующее. Функция y(x) всегда положительна, так как является суммой квадратов. Она имеет минимум при x=x_в, что следует из данных представленных на рис.2. Качественно функция y(x) изображена на рисунке 3.

Известно, что для нахождения экстремума функции необходимо приравнять нулю ее производную. Возьмем производную от функции (4) и приравняем её нулю.

(10)

Таким образом, истинное значение наиболее близко находится к наиболее вероятному значению x_в, которое равно среднему арифметическому , получаемое от нескольких идентичных измерений.

Обработка результатов прямого измерения

Учитывая вышеизложенное, можно рекомендовать следующий алгоритм обработки результатов прямых измерений.

1. Из-за наличия погрешностей никогда не следует ограничиваться одиночным измерением, а всегда следует проводить несколько опытов желательно нечетное число (три, пять).

(11)

3. Вычислить случайную абсолютную ошибку каждого измерения по уравнению (3):

а затем среднюю абсолютную погрешность:

(12)

4. Определить приборную погрешность, используя паспортные данные прибора или, при их отсутствии, принять за погрешность половину наименьшего деления шкалы стрелочного прибора или наименьший разряд цифрового прибора.

5. Сравнить приборную и среднюю абсолютную погрешность, выбрать большую из них, приняв за полную погрешность результаты измерения.

Окончательный результат можно представить в виде: Это означает, что истинное значение лежит в интервале .

Отработка результатов косвенных измерений

Метод частных производных

Пусть интересующая нас величина y является некоторой функцией других величин x_l, x₂, x₃ и т.д., так что

причем величины x_l, x₂, x₃. мы можем измерять путем прямых измерений. В этом случае мы для определения величин и ∆ сначала измеряем все величины, от которых зависит у (x_l, x₂, x₃. ) по методике, изложенной в предыдущем параграфе. В результате чего определяем , а также полные погрешности, в определении этих величин, которые обозначим как Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (13) наилучших (средних) значений

(14)

Для определения полной абсолютной погрешности величины у необходимо выяснить, как изменяется эта величина при относительно небольших изменениях всех величин, от которых зависит величина у. Это можно сделать с помощью полного дифференциала. Интересующее нас изменение величины

(15)

где — обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях и т.д.

От бесконечно малых изменений величин dу, dx_l, dx₂, dx₃. в (15) перейдем к конечным значениям их изменений (погрешностям) ∆у, ∆x_l, ∆x₂, ∆x₃.

(16)

Под частной производной функции ƒ(x, y, z) по переменной X понимают величину:

(17)

т.е. это производная, которая вычисляется в предположении, что все переменные, кроме той, по которой берется производная, являются постоянными величинами. Например: пусть . Тогда