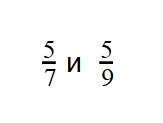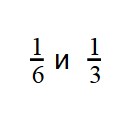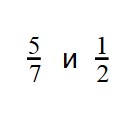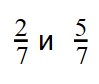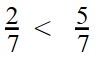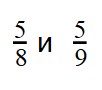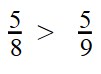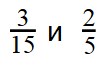как узнать какое число заключено между дробями
Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
Пример
Для примера сложим следующие дроби с равными знаменателями:
2 7 + 4 7 = 2 + 4 7 = 6 7
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
1 2 + 1 3 = 1⋅3 2⋅3 + 1⋅2 3⋅2 = 3 6 + 2 6 = 3+2 6 = 5 6
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
1 2 + 1 4 = 1⋅2 2⋅2 + 1 4 = 2 4 + 1 4 = 2+1 4 = 3 4
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
1 2 + 1 4 = 1⋅4 2⋅4 + 1⋅2 4⋅2 = 4 8 + 2 8 = 4+2 8 = 6 8 = 3 4
Обратите внимание, что мы сократили дробь:
6 8 = 3 ⋅ 2 4 ⋅ 2 = 3 4
Сложение смешанных чисел
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
Пример
Для примера сложим два смешанных числа:
3 1 2 + 1 2 3 = 1+3⋅2 2 + 2+1⋅3 3 = 7 2 + 5 3 = 7⋅3 2⋅3 + 5⋅2 3⋅2 = 21 6 + 10 6 = 21+10 6 = 31 6 = 5⋅6+1 6 = 5⋅6 6 + 1 6 = 5 1 6
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
31 6 = 5⋅6+1 6 = 5⋅6 6 + 1 6 = 5 1 6
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
Пример
Решим предыдущий пример этим способом:
3 1 2 + 1 2 3 = (3 + 1) + ( 1 2 + 2 3 ) = 4 + 1⋅3 2⋅3 + 2⋅2 3⋅2 = 4 + 3 6 + 4 6 = 4 + 3+4 6 = 4 + 7 6 = 4 + 1 1 6 = 5 1 6
Вычитание дробей
С одинаковыми знаменателями
Формула
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
3 5 − 2 5 = 3−2 5 = 1 5
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
3 4 − 1 3 = 3⋅3 4⋅3 − 1⋅4 3⋅4 = 9 12 − 4 12 = 9−4 12 = 5 12
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
Пример
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
1 3 ⋅ 2 3 = 1⋅2 3⋅3 = 2 9
Пример №2
Умножим дроби с разными знаменателями:
1 3 ⋅ 2 4 = 1⋅2 3⋅4 = 2 12 = 1⋅2 6⋅2 = 1 6
Пример №3
Умножим смешанные числа:
1 1 2 ⋅ 2 2 3 = 1+1⋅2 2 ⋅ 2+2⋅3 3 = 3 2 ⋅ 8 3 = 3⋅8 2⋅3 = 24 6 = 4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
2 3 : 1 3 = 2 3 ⋅ 3 1 = 2⋅3 3⋅1 = 6 3 = 2
Пример №2
Делим дроби с разными знаменателями:
1 2 : 2 3 = 1 2 ⋅ 3 2 = 1⋅3 2⋅2 = 3 4
Пример №3
Деление смешанных чисел:
4 1 2 : 2 2 3 = 1+4⋅2 2 : 2+2⋅3 3 = 9 2 : 8 3 = 9 2 ⋅ 3 8 = 9⋅3 2⋅8 = 27 16 = 1⋅16+11 16 = 1⋅16 16 + 11 16 = 1 11 16
Как найти число заключенное между дробями
Здесь легко и интересно общаться. Присоединяйся!
Таких чисел бесконечно много. Можете взять, например,
среднее: (1/3+1/2):2=5/6:2=5/12.
Их там целый континуум. Приводите обе дроби к одному знаменателю — для удобства — и получаете ответ.
Например: 1/3 = 2/6, 1/2 = 3/6
Значит, любое отношение двух чисел вида a/6, где a — из интервала (2, 3), будет расположено между дробями 1/3 и 1/2.
В частности, положим a = 2.5 и получим представителя в виде простой дроби: 25/60.
Второй случай полностью аналогичен только что разобранному.
Ответ оставил Гость
Задание 1. Найдите значение выражения 
Вычислим выражение, получим:

Задание 2. Какое из следующих чисел заключено между числами 17/15 и 16/13?
1) 1,2; 2) 1,3; 3) 1,4; 4) 1,5
Для определения чисел, которые попадают в диапазон между дробями, переведем дроби в десятичный вид, вычислим их до сотого знака, имеем:

то есть получаем диапазон от 1,13 до 1,23. В этот диапазон попадает число 1,2, записанное под номером 1.
Задание 3. Какое из данных чисел √0,64, √64, √6,4 является иррациональным?
1) √0,64; 2) √64; 3) √6,4; 4) все эти числа рациональны
Иррациональное число – это число обратное рациональному, то есть те, которые не могут быть выражены конечной десятичной дробью или бесконечной периодической дробью. Проанализируем, какие из приведенных чисел являются иррациональными:
1) 
2) 
3) 
Таким образом, получили одно иррациональное число под номером 3.
Задание 4. Решите уравнение 3x^2-9x = 0. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Перепишем уравнение в следующем виде:

которое будет равно 0, если
Получили два корня, больший из которых, равен 3.
Сравнение дробей, как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.
Давайте разберем наглядный пример сравнения дробей:
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Найдите разность:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Если знаменатели одинаковые — больше та дробь, числитель которой больше.
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: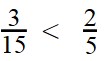
Какое из следующих чисел заключено между числами 9/19 и 5/9 1) 0.2 2) 0.3 3) 0.4 4)0.5
Ответ или решение 2
Определим какое из следующих чисел заключено между числами 9/19 и 5/9.
Сначала находим приближённое значение данных дробей.
1) 0.2. Данное число меньше, чем дробь 9/19.
2) 0.3. Данное число меньше чем дробь 9/19.
3) 0.4. Данное число меньше, чем 9/19.
4)0.5. Данное число больше, чем дробь 9/19, но меньше, чем дробь 9/19.
Следовательно, правильный вариант ответа номер номер 4.
При сравнении дробей необходимо сравнивать числители с одинаковыми знаменателями. Таким образом, все числа: и заданные границы интервала значений, и возможные ответы требуется привести к общему знаменателю.
Общий знаменатель дробей
По условию задания требуется сравнить следующие дроби: 9/19; 5/9; 0,2; 0,3; 0,4; 0,5.
Таким образом, наименьшее общее кратное для чисел 9, 10 и 19 является произведением всех этих чисел, так как ни один простой множитель не встречается в произведении данных чисел. Общий знаменатель равен 1710.
Дроби с одинаковым знаменателем
Дробь 9/19 нужно домножить на 90/90 и получается 810/1710;
остальные на 171/171: 342/1710; 513/1710; 684/1710; 855/1710.
В результате получается, что число 0,5 = 855/1710 находится в интервале от 810/1710 до 900/1710.
Ответ: число 0,5 заключено между числами 9/19 и 5/9.
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: