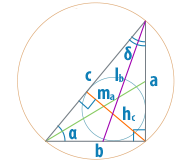
как узнать катет по гипотенузе и углу

Гипотенуза и угол «α» прямоугольного треугольника

Свойства

Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1) β=90°-α a=c sin⁡α b=c cos⁡α

Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов. P=a+b+c=c sin⁡α+c cos⁡α+c=c(sin⁡α+cos⁡α+1)

Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения. S=ab/2=(sin⁡α cos⁡α)/2

Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2) h=b sin⁡α=c cos⁡α sin⁡α

Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.3) m_с=c/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗⁡α+〖c^2 cos^2〗⁡α )/2=(с√(3 sin^2⁡α+1))/2 m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2⁡α+sin^2⁡α )/2=(с√(3 cos^2⁡α+1))/2

Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.4) l_с=(ab√2)/(a+b)=(c sin⁡α cos⁡α √2)/(sin⁡α+cos⁡α ) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cos⁡α √(2c(c cos⁡α+c) ))/(c cos⁡α+c)=(c cos⁡α √(2(cos⁡α+1) ))/(cos⁡α+1) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sin⁡α √(2c(c sin⁡α+c) ))/(c sin⁡α+c)=(c sin⁡α √(2(sin⁡α+1) ))/(sin⁡α+1)

Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7) M_a=a/2=(c sin⁡α)/2 M_b=b/2=(c cos⁡α)/2 M_c=c/2

Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее. Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два. Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6) r=(a+b-c)/2=(c sin⁡α+c cos⁡α-c)/2=c/2 (sin⁡α+cos⁡α-1) R=c/2

Источник

Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Источник

Калькулятор прямоугольного треугольника

Корзина

Как пользоваться онлайн-калькулятором. В форме укажите известные параметры прямоугольного треугольника:
а) 2 катета,
б) катет и гипотенуза,
в) катет и противолежащий острый угол,
г) гипотенуза и острый угол.
Заполните поле «Текст с картинки». Нажмите «Решить».

При помощи калькулятора прямоугольного треугольника можно найти гипотенузу онлайн, а также катеты, величины острых и противолежащих углов прямоугольного треугольника.

В форме калькулятора гипотенузы указываются два параметра прямоугольного треугольника онлайн: две стороны или острый угол и сторона.

Для углов имеются два поля: для градусов и для минут.

Далее заполнить поле «Текст с картинки» и нажать «Решить». Компьютерная программа автоматически сделает расчет.

Приводятся ответы с подробными решениями, включая формулы. Для решения задач используется теорема Пифагора. Катеты и гипотенуза вычисляются через синус.

Примеры решения калькулятора прямоугольного треугольника:
1) как найти неизвестный катет или катеты, если известна гипотенуза, равная 2 см, и острый угол 20°. В поле для гипотенузы «c» указывается 2, в поле «Угол (градусов, °)» ставится 20, в поле «Угол (минут, ‘)» указывается 0. Ответ онлайн калькулятора прямоугольного треугольника: длина катетов a = 0,68 см; b = 1,88 см, острый угол B = 70°.

2) пример вычисления неизвестных сторон и острых углов прямоугольного треугольника по двум катетам или по гипотенузе и катету. Вопрос: как найти угол прямоугольного треугольника, зная его стороны, т.е. зная 2 катета или 2 стороны. Известна длина катетов a=11, b=60.

В полях для катетов «a» указывается 11, в поле «b» 60. Нажать «Решить». В ходе решения находим третью сторону – гипотенузу – и находим угол в прямоугольном треугольнике, уже зная все стороны.

Ответ калькулятора гипотенузы: гипотенуза c=61, значения углов A= 10°23′, B = 79°37′. Если даны катет и гипотенуза, то заполняются поля для катета «a» и для гипотенузы «c».

3) с помощью этого онлайн-калькулятора можно решить задачу, где требуется найти катет онлайн, или как найти гипотенузу, зная катет и угол. Например, a=3, противолежащий угол = 30°27′. В поле для катетов «a» указывается 3, в поле «Угол (градусов, °)» ставится 30, в поле «Угол (минут, ‘)» указывается 27. Ответ калькулятора углов прямоугольного треугольника: гипотенуза c = 5,92; катет b = 5,10; угол 59°33’.

Калькулятор сторон прямоугольного треугольника может найти гипотенузу по катету и углу. Онлайн калькулятор гипотенузы находит катет по гипотенузе и углу.

Если стоит задача, как найти катет, если известна гипотенуза и угол, то можно использовать решение прямоугольного треугольника на этой странице. Гипотенузу прямоугольного треугольника, его угол быстро вычисляет компьютерная программа. Калькулятор теоремы Пифагора может найти катет по углу и катету.

Здесь предлагаются ответы на тесты, если требуется вычислить угол по двум катетам. Расчет гипотенузы выполняется онлайн.

Вычисление гипотенузы и углов прямоугольного треугольника при помощи калькулятора катетов дает ответы на следующие тестовые задания по теме «катет и гипотенуза«:
— как найти угол прямоугольного треугольника, зная его стороны,
— узнать гипотенузу, катет прямоугольного треугольника,
— определить гипотенузу по двум катетам,
— рассчитать третью сторону прямоугольного треугольника,
— вычислить катет, если известна гипотенуза и угол,
— найти решение прямоугольного треугольника,
— определить длину гипотенузы, зная 2 катета,
— посчитать угол в прямоугольном треугольнике,
— узнать гипотенузу по катетам,
— рассчитать величину угла в градусах и минутах по катетам,
— найти длину катета по катету и углу,
— вычислить угол или углы прямоугольного треугольника онлайн,
— решить прямоугольный треугольник,
— подсчитать угол по катетам,
— найти сторону прямоугольного треугольника,
— рассчитать прямоугольный треугольник онлайн.

Источник

Катет «A» и угол «α» прямоугольного треугольника

Свойства

Зная один из катетов в прямоугольном треугольнике, можно найти второй катет и гипотенузу используя тригонометрические отношения – синус и тангенс известного угла. Так как отношение противолежащего углу катета к гипотенузе равно синусу этого угла, следовательно, чтобы найти гипотенузу нужно катет разделить на синус угла. a/c=sin⁡α c=a/sin⁡α

Второй катет можно найти из тангенса известного угла, как отношение известного катета к тангенсу. a/b=tan⁡α b=a/tan⁡α

Чтобы вычислить неизвестный угол в прямоугольном треугольнике нужно из 90 градусов вычесть величину угла α. β=90°-α

Периметр и площадь прямоугольного треугольника через катет и противолежащий ему угол можно выразить, подставив полученные ранее выражения для второго катета и гипотенузы в формулы. P=a+b+c=a+a/tan⁡α +a/sin⁡α =a tan⁡α sin⁡α+a sin⁡α+a tan⁡α S=ab/2=a^2/(2 tan⁡α )

Вычислить высоту также можно через тригонометрические отношения, но уже во внутреннем прямоугольном треугольнике со стороной a, который она образует. Для этого нужно сторону a, как гипотенузу такого треугольника умножить на синус угла β или косинус α, так как согласно тригонометрическим тождествам они равнозначны. (рис. 79.2) h=a cos⁡α

Медиана гипотенузы равна половине гипотенузы или известному катету a, деленному на два синуса α. Чтобы найти медианы катетов, приведем формулы к соответствующему виду для известной стороны и углы. (рис.79.3) m_с=c/2=a/(2 sin⁡α ) m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4a^2+a^2/tan^2⁡α )/2=(a√(4 tan^2⁡α+1))/(2 tan⁡α ) m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4b^2+a^2 )/2=√(4b^2+c^2-b^2 )/2=√(3 a^2/tan^2⁡α +a^2/sin^2⁡α )/2=√((3a^2 sin^2⁡α+a^2 tan^2⁡α)/(tan^2⁡α sin^2⁡α ))/2=(a√(3 sin^2⁡α+tan^2⁡α ))/(2 tan⁡α sin⁡α )

Так как биссектрисой прямого угла в треугольнике является произведение двух сторон и корня из двух, деленное на сумму этих сторон, то заменив один из катетов на отношение известного катета к тангенсу, получаем следующее выражение. Аналогично, подставив отношение во вторую и третью формулы, можно вычислить биссектрисы углов α и β. (рис.79.4) l_с=(a a/tan⁡α √2)/(a+a/tan⁡α )=(a^2 √2)/(a tan⁡α+a)=(a√2)/(tan⁡α+1) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(a/tan⁡α √(2c(a/tan⁡α +c) ))/(a/tan⁡α +c)=(a√(2c(a/tan⁡α +c) ))/(a+c tan⁡α ) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(a√(2c(a+a/sin⁡α ) ))/(a+a/sin⁡α )=(a sin⁡α √(2c(a+a/sin⁡α ) ))/(a sin⁡α+a)

Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tan⁡α ) M_c=c/2=a/(2 sin⁡α )

Источник