как узнать количество степеней свободы

Степени свободы (механика)

Из Википедии — свободной энциклопедии

Сте́пени свобо́ды в механике — совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела (а вместе с их производными по времени — соответствующими скоростями — полностью определяющая состояние механической системы или тела, то есть их положение и движение).

В отличие от обычных декартовых или какого-то другого типа координат, такие координаты в общем случае называются обобщёнными координатами (декартовы, полярные или какие-то другие конкретные координаты являются, таким образом, частным случаем обобщённых). По сути речь идет о минимальном наборе чисел, который полностью определяет текущее положение (конфигурацию) данной системы.

Требование минимальности этого набора или независимости координат означает, что подразумевается набор координат, необходимый для описания положения системы лишь при возможных движениях (например, если рассматривается математический маятник, подразумевается, что его длина не может меняться, и таким образом координата, которая характеризует расстояние от груза до точки подвеса, не является его степенью свободы, так как не может меняться — то есть количество степеней свободы математического маятника в пространстве 2, а такого же маятника, который может двигаться только в одной плоскости, 1. Им соответствуют углы отклонения маятника от вертикали).

В случае, когда рассматривается система со связями (точнее говоря, с удерживающими связями), количество степеней свободы механической системы меньше, чем количество декартовых координат всех материальных точек системы, а именно:

Количество степеней свободы зависит не только от природы реальной системы, но и от модели (приближения), в рамках которых система изучается. Даже в приближении классической механики (в которых в целом и написана данная статья), если отказаться от использования дальнейших приближений, упрощающих задачу, количество степеней свободы любой макроскопической системы окажется огромным. Поскольку связи не бывают абсолютно жесткими (то есть на самом деле их можно рассматривать как связи лишь в рамках определённого приближения), то настоящее количество степеней свободы механической системы можно оценить как минимум как утроенное количество атомов (а в приближении сплошной среды — как бесконечное). Однако на практике используют приближения, позволяющие радикально упростить задачу и уменьшить количество степеней свободы при рассмотрении системы, поэтому в практических расчетах количество степеней свободы — конечное, обычно достаточно небольшое, число.

Источник

Степени свободы: как их вычислить, виды, примеры

Содержание:

Концепция чего-либо степени свободы он также появляется в теоретической механике, где они примерно эквивалентны измерению пространства, в котором движется частица, за вычетом количества связей.

В этой статье будет обсуждаться концепция степеней свободы, применяемая к статистике, но механический пример легче визуализировать в геометрической форме.

Типы степеней свободы

В зависимости от контекста, в котором он применяется, способ вычисления количества степеней свободы может варьироваться, но основная идея всегда одна и та же: общие размеры минус количество ограничений.

В механическом корпусе

Давайте рассмотрим колеблющуюся частицу, привязанную к веревке (маятник), которая движется в вертикальной плоскости x-y (2 измерения). Однако частица вынуждена двигаться по окружности с радиусом, равным длине струны.

Поскольку частица может двигаться только по этой кривой, количество степени свободы ru 1. Это можно увидеть на рисунке 1.

Чтобы рассчитать количество степеней свободы, нужно взять разность количества измерений за вычетом количества ограничений:

Еще одно объяснение, которое позволяет нам прийти к результату, заключается в следующем:

-Мы знаем, что положение в двух измерениях представлено точкой с координатами (x, y).

-Но так как точка должна удовлетворять уравнению окружности (x 2 + и 2 = L 2 ) для данного значения переменной x переменная y определяется указанным уравнением или ограничением.

Таким образом, только одна из переменных является независимой, и система имеет одна (1) степень свободы.

В наборе случайных значений

Чтобы проиллюстрировать, что означает эта концепция, предположим, что вектор

Что представляет собой образец п нормально распределенные случайные величины. В этом случае случайный вектор Икс иметь п независимые компоненты, и поэтому говорят, что Икс иметьn степеней свободы.

Теперь построим вектор р отходов

куда представляет собой выборочное среднее значение, которое рассчитывается следующим образом:

Это уравнение, которое представляет собой ограничение (или привязку) к элементам вектора. р остатков, поскольку, если известны n-1 компонент вектора р, уравнение ограничения определяет неизвестную составляющую.

Следовательно, вектор р размерности n с ограничением:

Снова применяется, что вычисление числа степеней свободы:

Примеры

Дисперсия и степени свободы

Дисперсия s 2 определяется как среднее значение квадрата отклонений (или остатков) выборки из n данных:

s 2 = (р•р) / (п-1)

В любом случае следует отметить, что при вычислении среднего квадрата остатков оно делится на (n-1), а не на n, поскольку, как обсуждалось в предыдущем разделе, количество степеней свободы вектора р равно (n-1).

Если для расчета дисперсии разделить на п вместо (n-1) результат будет иметь смещение, которое очень важно для значений п до 50.

В литературе формула дисперсии также встречается с делителем n вместо (n-1), когда речь идет о дисперсии генеральной совокупности.

Но набор случайной величины остатков, представленный вектором р, Хотя он имеет размерность n, он имеет только (n-1) степеней свободы. Однако, если количество данных достаточно велико (n> 500), обе формулы сходятся к одному и тому же результату.

Калькуляторы и электронные таблицы предоставляют обе версии дисперсии и стандартного отклонения (которое является квадратным корнем из дисперсии).

В распределении хи-квадрат

Название этого параметра происходит именно от степеней свободы базового случайного вектора, к которому применяется это распределение.

Предположим, у нас есть g популяций, из которых взяты выборки размера n:

Население j что среднее и стандартное отклонение Sj,следует нормальному распределению N ( , Sj ).

Стандартизированная или нормализованная переменная zj_я определяется как:

И вектор Zj определяется так:

Zj = (zj₁, zj₂,…, Zj_я,…, Zj_п) и следует стандартизованному нормальному распределению N (0,1).

следовать распределению χ 2 (g) назвал распределение хи-квадрат со степенью свободы грамм.

При проверке гипотез (с проработанным примером)

Если вы хотите проверить гипотезу на основе определенного набора случайных данных, вам необходимо знать число степеней свободы g чтобы иметь возможность применять критерий хи-квадрат.

В качестве примера будут проанализированы собранные данные о предпочтениях мужчин и женщин в отношении шоколадного или клубничного мороженого в определенном кафе-мороженом. Частота, с которой мужчины и женщины выбирают клубнику или шоколад, представлена ​​на Рисунке 2.

Сначала рассчитывается таблица ожидаемых частот, которая составляется путем умножения всего строк для негоитоговые столбцы, деленное на общие данные. Результат показан на следующем рисунке:

Затем мы приступаем к вычислению хи-квадрат (по данным) по следующей формуле:

После выполнения операций вы получаете:

Теперь необходимо сравнить с теоретическим Хи-квадрат, который зависит от число степеней свободы g.

В нашем случае это число определяется следующим образом:

Оказывается, число степеней свободы g в этом примере равно 1.

Если вы хотите проверить или отклонить нулевую гипотезу (H0: нет корреляции между ВКУСОМ и ПОЛОМ) с уровнем значимости 1%, теоретическое значение хи-квадрат рассчитывается со степенью свободы g = 1.

Когда теоретическая Чи превышает расчетную, нулевая гипотеза проверяется.

То есть с собранными даннымиНе наблюдается взаимосвязь между переменными ВКУС и ГЕНДЕР.

Ссылки

Эйзоптрофобия, страх саморефлексии: симптомы и что делать

Источник

О степенях свободы в статистике

В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.

Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?

По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.

Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:

Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:

Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.

Но почему n минус один?

Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?

В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:

“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.

Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?

Причем тут распределение Хи-квадрат Пирсона?

Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:

имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.

Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?

Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:

Где O — наблюдаемые, E — ожидаемые частоты.

Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.

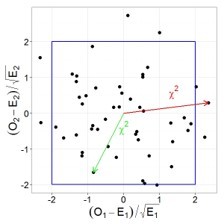
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:

При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.

Пришло время вычесть единичку!

Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.

Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.

Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.

Все становится на свои места

Теперь, вооружившись этими знаниями, вернемся к t-тесту:

в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.

Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.

Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.

Онлайн курсы по статистике: объясняем сложные темы простым языком

Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.

Источник

Физика Б1.Б8.

Молекулярная физика и термодинамика

1. Введение

Основы молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана, Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика прочно утвердилась в науке. Непосредственным опытным подтверждением молекулярно-кинетической теории являются процесс диффузии, броуновского движения, распространения запаха и многие другие явления.

Движение каждой молекулы в веществе может быть описано законами классической механики. Однако число молекул в веществе чрезвычайно велико, направления и величины скоростей молекул совершенно случайны и непрерывно изменяются так, что становится невозможным охватить уравнениями движения всю совокупность молекул и сделать какие-либо выводы об их поведении.

Тем не менее, состояние вещества и его изменение определяется заданием небольшого числа определенных параметров, как температура, давление, объем, плотность и т.д., значения которых невозможно указать на основе решений уравнений классической механики. Дело в том, что свойства огромного числа молекул подчиняется особым, статистическим закономерностям. Статистическая физика изучает статистические закономерности, описывающие поведение большой совокупности объектов. Она основывается на теории вероятностей и позволяет вычислять средние значения величин, характеризующих движение всей совокупности молекул (средние скорости молекул, средние кинетические энергии, средние значения импульса и т. д.) и на этой основе истолковывает свойства вещества, непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом состоит суть молекулярно-кинетического изучения вещества.

Наряду со статистическим, существует термодинамический метод изучения вещества. В отличие от статистического метода термодинамический метод не интересуется строением вещества. Термодинамика изучают условия превращения энергии и характеризует их с количественной стороны.

В основе термодинамики лежит небольшое число закономерностей, установленных на основе большого числа опытных фактов и получивших название начала термодинамики.

У статистической физики и термодинамики общий предмет изучения – свойства вещества и происходящие в нем процессы. Подходя к изучению этих свойств с разных точек зрения, эти методы взаимно дополняют друг друга.

Совокупность тел, могущих обмениваться энергией между собой и с внешними телами, не входящими в эту систему, называется термодинамической системой. Одним из основных понятий термодинамики является понятие состояния системы. Состояние системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых термодинамическими параметрами (температура, давление плотность, теплоемкость, электропроводность и т. д.). Состояние системы называется стационарным, если значения всех термодинамических параметров не изменяются во времени. Стационарное состояние называется равновесным, если его неизменность не обусловлена протеканием каких-либо процессов во внешних по отношению к данной системе телах.

Исследования показывают, что параметры состояния тел взаимно связаны и могут быть выражены друг через друга. Поэтому термодинамическое состояние задается только ограниченным числом параметров состояния. Такие параметры называются основными параметрами состояния. Важнейшими параметрами состояния химически однородных систем являются плотность, объем, давление, температура. И между этими параметрами существует связь, выражаемая в виде математического уравнения . Уравнение, связывающее основные параметры состояния, называется уравнением состояния системы.

Источник