как узнать квадратные метры треугольника
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
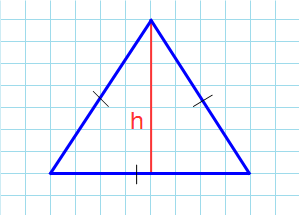
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
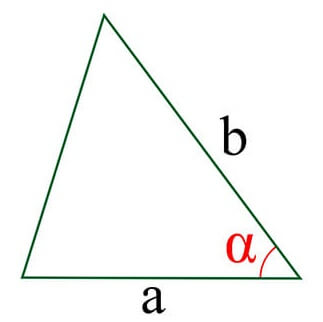
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
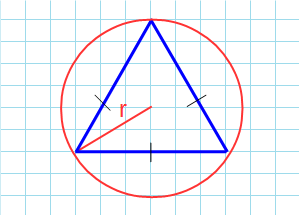
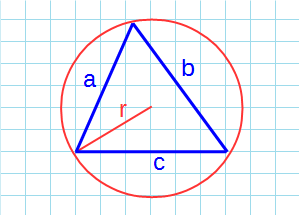
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
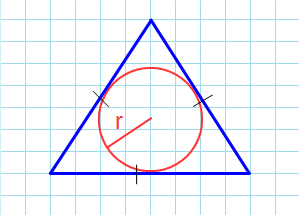
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Как найти площадь треугольника
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
1. Площадь треугольника через две стороны и угол между ними.
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
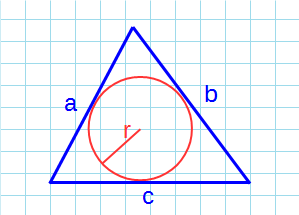
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Калькулятор расчета площади треугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади треугольника по разным исходным данным: через основание и высоту, три стороны, две стороны и угол между ними, три стороны и радиус вписанной или описанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.
1. Через основание и высоту
Формула расчета
2. Через длину трех сторон (формула Герона)
Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).
Формула расчета:
p – полупериметр, который считается так:
3. Через две стороны и угол между ними
Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).
Калькулятор площади треугольника
Скачать, сохранить результат
Выберите способ сохранения
Информация
В современном мире не возможно представить человека, который не сталкивался с площадью треугольника. Еще в начальной школе учат этим знаниям. Особенно важны эти знания в различных сферах деятельности человека. Например, строитель (инженер, техник или проектировщик) не может не знать как искать площадь прямоугольного треугольника. Это может пригодиться при расчете размера покупки нужного количества материала для того или иного объекта.
Как найти площадь треугольника онлайн?
Для того, чтобы избавить специалистов различных отраслей от навязчивого вопроса «Как найти площадь треугольника?» и обезопасить их от допущения ошибок в процессе расчета, которые могу привести к катастрофическим последствиям, мы создали калькулятор онлайн. В наш калькулятор встроена формула для поиска площади любого треугольника по любым исходным данным. Благодаря этому инструменту, Вы можете найти площадь равнобедренного треугольника менее, чем за 5 секунд. Также калькулятор мгновенно рассчитывает площадь равностороннего треугольника, которая может находится как площадь правильного треугольника, поскольку равносторонний треугольник является правильным.
Треугольник – основная геометрическая фигура, состоящая из трех отрезков, которые соединяются в точках (вершинах) треугольника.
Существует две классификации треугольника
По углам:
По сторонам:
Калькулятор поможет рассчитать площадь через синус и сообщит Вам чему равна площадь данного треугольник, что доказывает универсальность нашего калькулятора, который является незаменимым в определенных ситуациях. В его программу внесен способ расчета площади треугольника по трем сторонам, что позволяет искать площадь Вашего треугольника через стороны.
Таким образом, созданный нами калькулятор, позволяет избавить людей от риска возникновения ошибки, которая могла бы привести к очень плохим последствиям. Экономит время, поскольку нет необходимости тратить его на самостоятельное вычисление нужного показателя. И важным преимуществом является то, что калькулятор включает в расчет площади треугольник любой его вид и применяет любую формулу.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
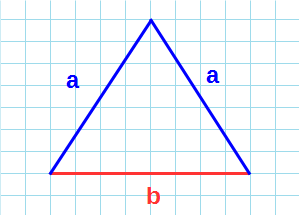
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
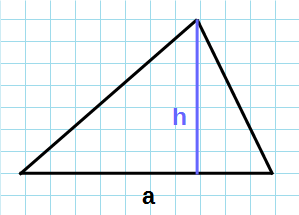
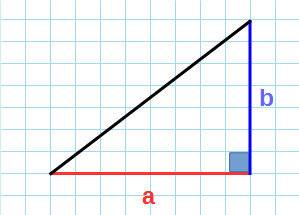
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
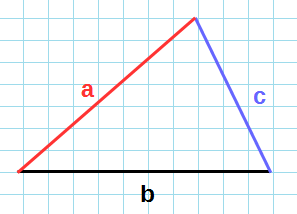
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.