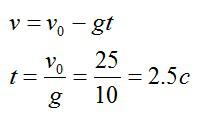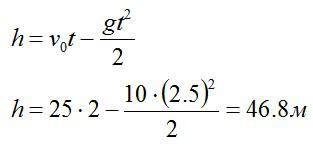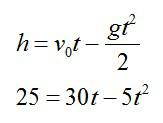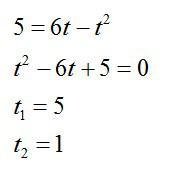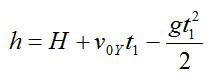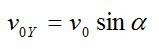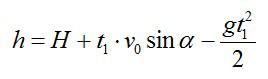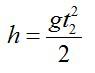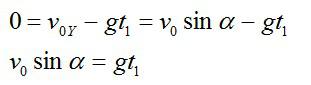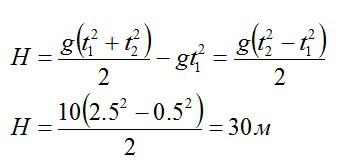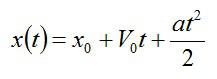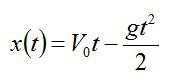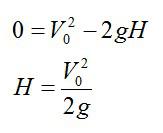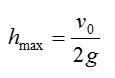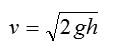как узнать начальную скорость
Основы механики для чайников. Часть 1: Кинематика
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Начальная скорость
Начальная скорость пули — скорость движения пули у дульного среза ствола.
При увеличении начальной скорости увеличивается дальность полета пули, дальность прямого выстрела, убойное действие пули и пробивное действие пули, а также уменьшается влияние внешних условий на ее полет.
Величина начальной скорости пули зависит от следующих параметров:
Влияние изменения длины ствола на начальную скорость пули
Влияние качества порохового заряда и изменения величины порохового заряда на начальную скорость пули
Смотреть что такое «Начальная скорость» в других словарях:
Начальная скорость — скорость поступательного движения снаряда (мины) у дульного среза ствола орудия или скорость снаряда (мины) в точке вылета из ствола орудия (миномета). Н. с. для данной системы орудия зависит от веса заряда и снаряда, от длины ствола, качества … Краткий словарь оперативно-тактических и общевоенных терминов
Начальная скорость — расчетная скорость поступательного движения снаряда (мины, пули) у дульного среза ствола. Измеряется в м/с. Указывается в таблицах стрельбы EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
начальная скорость — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN initial velocityiv … Справочник технического переводчика
начальная скорость — pradinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno greitis pradinę arba atskaitos akimirką. atitikmenys: angl. initial velocity vok. Anfangsgeschwindigkeit, f rus. начальная скорость, f pranc. vitesse initiale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
начальная скорость — pradinis greitis statusas T sritis chemija apibrėžtis Greitis proceso pradžioje. atitikmenys: angl. initial velocity rus. начальная скорость … Chemijos terminų aiškinamasis žodynas
начальная скорость — pradinis greitis statusas T sritis Gynyba apibrėžtis Didžiausias sviedinio (kulkos) greitis. Suteikiamas sviediniui (kulkai) judant vamzdžio kanalu ir parako dujų poveikiminiu šūvio periodu, t. y. tam tikru nuotoliu nuo vamzdžio. Pradinis greitis … Artilerijos terminų žodynas
начальная скорость — pradinis greitis statusas T sritis fizika atitikmenys: angl. initial velocity vok. Anfangsgeschwindigkeit, f rus. начальная скорость, f pranc. vitesse initiale, f … Fizikos terminų žodynas
начальная скорость — pradinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Bėgiko, čiuožėjo, slidininko pirmojo žingsnio po starto ženklo greitis. atitikmenys: angl. initial speed vok. Anfangsgeschwindigkeit, f; Anfangstempo, n rus. начальная скорость … Sporto terminų žodynas
начальная скорость — pradinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Kulkos išlėkimo iš vamzdžio greitis. atitikmenys: angl. initial speed vok. Anfangsgeschwindigkeit, f; Anfangstempo, n rus. начальная скорость … Sporto terminų žodynas
начальная скорость — pradinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Metimo įrankio (ieties, disko, kūjo) lėkimo tik atitrūkus nuo rankos (rankų) greitis. atitikmenys: angl. initial speed vok. Anfangsgeschwindigkeit, f; Anfangstempo, n rus.… … Sporto terminų žodynas
Задачи на свободное падение тел: примеры решения задач по кинематике
Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».
Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!
Задачи на свободное падение тел с решением
Задача №1. Нахождение скорости при свободном падении
Условие
Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?
Решение
Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:
Ответ: примерно 20 метров в секунду.
Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.
Условие
Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?
Решение
Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:
Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.
Ответ: 2,5 секунды, 46 метров.
Задача №3. Нахождение времени движения тела, брошенного вертикально вверх
Условие
Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?
Решение
Запишем уравнение для движения мячика:
Мы получили квадратное уравнение. Упростим его и найдем корни:
Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).
Ответ: 1с, 5с.
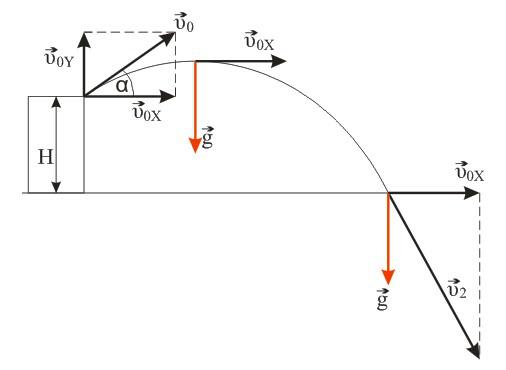
Задача №4. Нахождение высоты при движении тела под углом к горизонту
Условие
Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.
Решение
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):
Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.
Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:
Подставив выражение для скорости в первое уравнение, получим:
Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):
Для высоты дома можно записать:
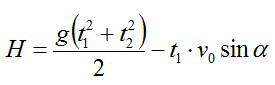
Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:
Подставляем в формулу для высоты H и вычисляем:
Ответ: H = 30 м.
Задача №5. Нахождение закона движения тела
Условие
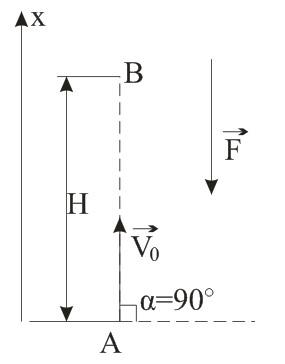
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.
Решение
Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.
В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:
где х0 – начальная координата тела; a – ускорение.
Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:
Далее будем использовать еще одно общее кинематическое соотношение:
где V – конечная скорость.
Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:
Полезные формулы для решения задач на свободное падение
Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.
Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:
Кстати, как выводится именно эта формула можно посмотреть в последней задаче.
Формула для времени подъема и падения тела, брошенного вертикально вверх:
Скорость тела в момент падения с высоты h:
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Вопросы с ответами на свободное падение тел
Вопрос 1. Как направлен вектор ускорения свободного падения?
Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.
Вопрос 2. От чего зависит ускорение свободного падения?
Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:
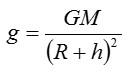
Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?
Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.
Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?
Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.
Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.
Вопрос 5. Что значит «свободное» падение.
Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.
Свободное падение тел: определения, примеры
Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.
Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.
Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.
Ускорение свободно падающих тел не зависит от их массы.
Примеры свободного падения тел:
При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.
Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.
При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.
Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.
Калькулятор движения снаряда
Наш калькулятор движения тела – это инструмент, который поможет вам проанализировать параболическое движение тела. Он может определить время полета, а также компоненты скорости, дальность полета и максимальную высоту полета. Продолжайте читать, если вы хотите понять, что такое движение тела, познакомьтесь с определением движения и определите вышеупомянутые значения с помощью уравнений движения тела.
Что такое движение тела (снаряда)? Определение движения снаряда
Анализ движения снаряда
Движение снаряда довольно логично. Предположим, вы знаете начальную скорость объекта V, угол запуска α и начальную высоту h. Наш калькулятор движения снаряда выполняет следующие действия, чтобы найти все оставшиеся параметры:
1. Вычислите составляющие скорости.
Три вектора – V, Vx и Vy – образуют прямоугольный треугольник.
Если вертикальная составляющая скорости равна 0, то это случай горизонтального движения снаряда. Если дополнительно α = 90 °, то это случай свободного падения.
2. Запишите уравнения движения.
Расстояние
3.Рассчитайте время полета.
t = 2 * Vy / g = 2 * V * sin (α) / g.
Однако, если мы бросаем объект с некоторой возвышенности, тогда формула не так хорошо сокращается, как раньше, и мы получаем квадратное уравнение для решения: h + Vy * t – g * t² / 2 = 0. После решения этой задачи уравнение, получаем:
t = [V * sin (α) + √ ((V * sin (α)) ² + 2 * g * h)] / g
4. Рассчитайте дальность полета снаряда.
График движения снаряда: дальность
Дальность полета снаряда – это общее горизонтальное расстояние, пройденное за время полета. Опять же, если мы запускаем объект с земли (начальная высота = 0), то мы можем записать формулу как R = Vx * t = Vx * 2 * Vy / g. Его также можно преобразовать в форму: R = V² * sin (2α) / g
Ситуация усложняется для начального значения высоты, отличного от 0. Затем нам нужно заменить длинную формулу из предыдущего шага на t:
R = Vx * t = V * cos (α) * [V * sin (α) + √ (V * sin (α)) ² + 2 * g * h)] / g
5. Рассчитайте максимальную высоту.
График движения снаряда: максимальная высота
Если Vy – g * t (Vy = 0) = 0, то мы можем переформулировать это уравнение к t (Vy = 0) = Vy / g.
Теперь мы просто находим расстояние по вертикали от земли в это время: hmax = Vy * t (vy = 0) – g * (t (Vy = 0)) ² / 2 = Vy² / (2 * g) = V² * sin (α) ² / (2 * г)
К счастью, в случае запуска снаряда с некоторой начальной высоты h нам нужно просто добавить это значение в окончательную формулу: hmax = h + V² * sin (α) ² / (2 * g)
Уравнения движения снаряда
Уфф, это было много вычислений! Подведем итог, чтобы сформировать наиболее важные уравнения движения снаряда:
Запуск объекта с земли (начальная высота h = 0)
Запуск объекта с некоторой высоты (начальная высота h> 0)
Использование нашего калькулятора движения снаряда наверняка сэкономит вам много времени. Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту и смотрите, как он выполняет все вычисления за вас!
Часто задаваемые вопросы
Нет, движение снаряда и его уравнения охватывают все движущиеся объекты, где единственной силой, действующей на них, является гравитация. Сюда входят объекты, которые подбрасываются прямо вверх, те, которые выбрасываются горизонтально, те, которые имеют горизонтальный и вертикальный компонент, и те, которые просто отбрасываются.
Как найти ускорение при движении снаряда?
Какие факторы влияют на движение снаряда, выпущенного горизонтально?
Каковы характеристики движения снаряда?
Свойства движения снаряда заключаются в том, что горизонтальная скорость объекта не изменяется, что его вертикальная скорость постоянно изменяется из-за силы тяжести, что форма его траектории будет параболой и что на объект не влияет сопротивление воздуха.
Кто первым и когда точно описал движение снаряда?
Галилей был первым человеком, который точно описал движение снаряда, разбив движение на горизонтальную и вертикальную составляющие и осознав, что график движения любого объекта всегда будет параболой. Он описал это в своей книге «О движении», опубликованной примерно в 1590-х годах.
Объект следует параболе из-за того, что гравитация влияет на две его составляющие движения – горизонтальную и вертикальную. Горизонтальная составляющая вообще не подвержена влиянию силы тяжести, поэтому изменяется линейно. Однако вертикальная часть постоянно находится под действием силы тяжести, поэтому она будет увеличиваться в высоте, а затем уменьшаться, ускоряясь под действием силы тяжести.
Почему 45 градусов – оптимальный угол для снарядов?
Уравнение для расстояния, пройденного снарядом под действием силы тяжести, имеет вид sin (2θ) v2 / g, где θ – угол, v – начальная скорость, а g – ускорение свободного падения. Предполагая, что v2 / g постоянна, наибольшее расстояние будет, когда sin (2θ) будет максимальным, то есть когда 2θ = 90 градусов. Это означает θ = 45 градусов.