как узнать направление ветвей параболы
Парабола в математике: уравнение, построение, виды
Что такое парабола в математике
Формула параболы может рассказать нам о многом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Алгоритм построения параболы
Построим график функции \(f(x)=ax^2+bx+c.\)
Примеры решения задач на построение параболы
Смещение параболы
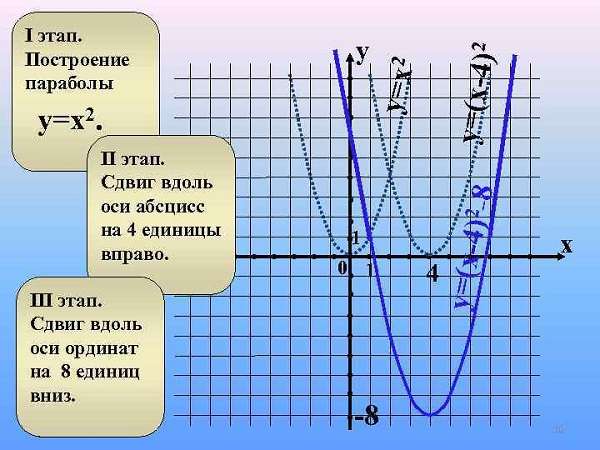
Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.
В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции \(y=<(x+4)>^2\) достаточно сместить график \(y=x^2 \) на 4 единичных отрезка влево, а для построения графика \(y=<(x-3)>^2\) нужно сместить график \(y=x^2\) на 3 единичных отрезка вправо.
Что такое Парабола
Определение Параболы
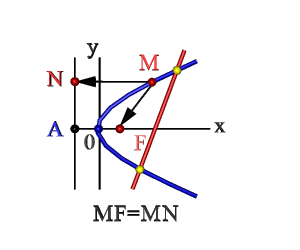
Парабола (от греч. παραβολή — сравнение, приближение, кривая линия) — в геометрии это плоская кривая линия (в форме арки), где каждая из точек M (на рисунке ниже) равноудалена от неподвижной точки F (фокус) и от неподвижной линии DA, называемой директрисой (MF = MA).
Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается как p.
В литературе парабола — это аллегория, под которой скрывается важная истина.
Как выглядит парабола, когда меняется фокальный параметр (p)
Изменения фокального параметра, когда фокус находится на оси OX:
Изменения фокального параметра, когда фокус находится на оси OY:
Квадратичная функция и как построить график параболы
Квадратичная функция выглядит следующим образом:
y = ax² + bx + c, где a≠0
(a — старший коэффициент; b — второй коэффициент; с — свободный член).
Построение графика квадратичной функции
Шаги построения графика
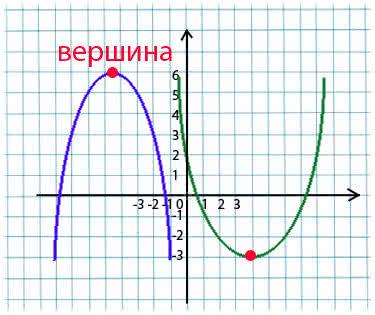
1. Как определить, куда направлены ветви параболы
Т. е. a (старший коэффициент) в данном случае равен 1, b (второй коэффициент) и c (свободный член) оба равны 0.
Ветви параболы будут направлены вверх, когда a > 0.
А в данном случае a = –1 (b = 0, с = 0).
Ветви параболы будут направлены вниз, когда a 0, то у квадратичной параболы будут две точки пересечения с осью ОХ, которые можно найти по этим формулам:
3. Как вычислить координаты вершины параболы
Формулы для их вычисления:
4. Как посчитать точку пересечения параболы с осью OY
Точка пересечения параболы с осью OY имеет координаты (0;c). Так как абсцисса любой точки, лежащей на оси OY, равна нулю.
Чтобы найти точку пересечения параболы с осью OY, нужно всего лишь в вашу формулу вида ax² + bx + c вместо х подставить ноль.
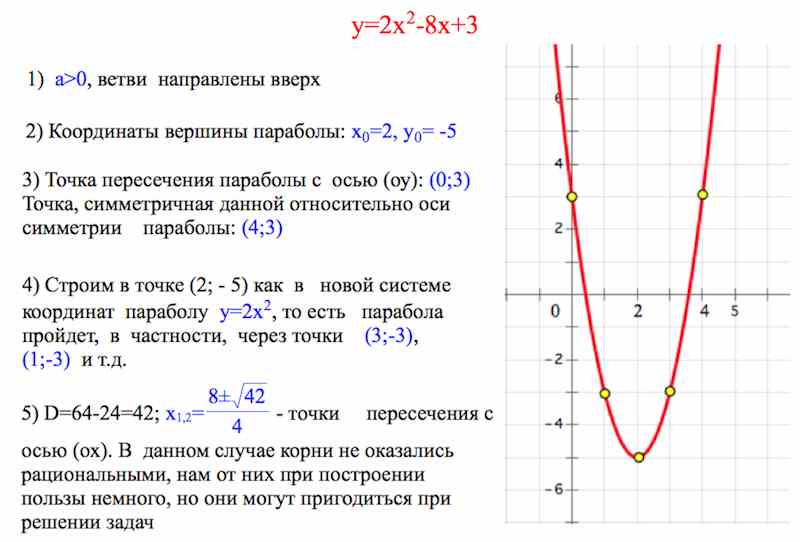
Пример построения графика квадратичной функции
Например, нужно построить график квадратичной функции y = x² − 7x + 10.
1) Если квадратичная функция выглядит как y = ax² + bx + c, получается, в нашем случае: a = 1, b = −7, c = 10.
a = 1, а это a > 0, следовательно ветви параболы будут направлены вверх
2) Определяем нули функции, это значит ax² + bx + c = 0, в нашем случае: x² − 7x + 10 = 0
Ищем дискриминант по формуле: D = b² − 4ac, это D = (−7)² − 4*1*10 = 49 − 40 = 9
Потом вычисляем х1 и х2:
х1 = (−b + ²√D) / 2a = (7 + ²√9) / (2*1) = 5
х2 = (−b − ²√D) / 2а = (7 − ²√9) / (2*1) = 2
3) Вычисляем координаты вершины параболы:
х0 = −b / 2a = 7 / (2*1) = 3,5
y0 = −D / 4а = −9 / (4*1) = −2,25
4) Точка пересечения параболы с осью OY имеет координаты (0;c), следовательно, если c = 10, она пересекает её на (0;10).
Таким образом, получилась парабола такого вида:
Свойства квадратичной функции y = x²
График функции y = x² выглядит следующим образом:
Свойства
1) Область определения функции y = x² — множество всех действительных чисел, т. е. D(y) = R = (−∞; +∞).
2) Множество значений функции — положительная полупрямая: E(y) = [0; +∞).
3) В точке x = 0 (и y = 0) функция принимает минимальные значения (наибольшего значения у функции нет).
Эта точка (с координатами (0;0)) является вершиной параболы; одновременно точка (0;0) является единственной общей точкой параболы с осями координат (начало координат).
4) Функция у = x² чётная, график симметричен относительно оси Оу, т. е. f(−x) = (−x)² = x² = f(x).
5) Функция непрерывна на всей области определения. На (−∞; 0) функция монотонно убывает, а на (0; + ∞) функция монотонно возрастает.
6) Функция у = x² непериодическая.
7) Единственный нуль функции — значение аргумента x = 0.
8) Функция у = x² не имеет асимптот.
9) Функция принимает положительные значения на всех точках параболы, кроме начала координат, т. е. в: (−∞;0) ∪ (0;+∞).
Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
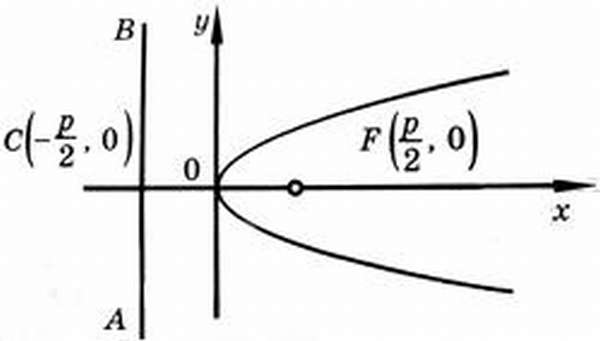
Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
Получаем алгоритм построения параболы:
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
По полученным точкам можно построить параболу.
Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Эксцентриситет (константа) = 1.
Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
Квадратичная функция. Парабола
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Квадратичная функция — это функция вида
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
Как построить график квадратичной функции
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции « y = x 2 −7x + 10 ».
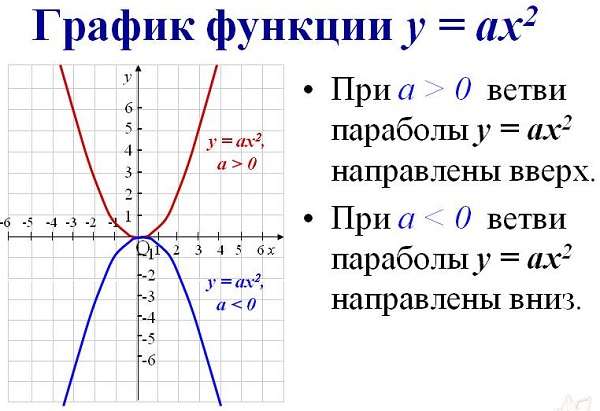
Если « a > 0 », то ветви направлены вверх.
Если « a », то ветви направлены вниз.
В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.
Чтобы найти « x0 » (координата вершины по оси « Ox ») нужно использовать формулу:
Найдем « x0 » для нашей функции « y = x 2 −7x + 10 ».
Теперь нам нужно найти « y0 » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x0 » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».
Для начала давайте разберемся, что называют нулями функции.
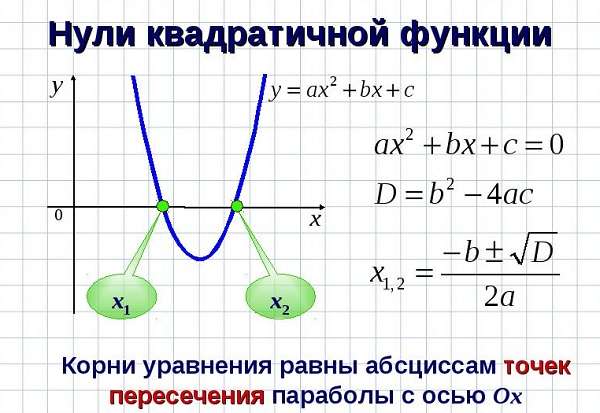
Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».
0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x1;2 =
| 7 ± √ 49 − 4 · 1 · 10 |
| 2 · 1 |
x1;2 =
| 7 ± √ 9 |
| 2 |
x1;2 =
| 7 ± 3 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 5 | x2 = 2 |
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.
Отметим полученные точки («нули функции») на системе координат.
Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
Для каждого выбранного значения « x » рассчитаем « y ».
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
x0 =
| −b |
| 2a |
x0 =
| −(−6) |
| 2 · (−3) |
=
| 6 |
| −6 |
= −1
y0(−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
x1;2 =
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
x1;2 =
| −6 ± √ 36 − 48 |
| 2 |
x1;2 =
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.
Квадратичная функция. Построение Параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Как строим: