как узнать нечетное число
Определить чётное или нечётное число
Сколько чётных и нечётных чисел между.
Теория
Чётное ли число
Чётным является целое число, которое делится на 2 без остатка (нацело).
Все многозначные числа, оканчивающиеся на 0,2,4,6 или 8, являются чётными числами:
Примеры
Чётное ли число 10?
Десять разделилось на два без остатка, следовательно 10 является чётным числом.
После деления единицы на два мы получаем нецелое число, следовательно 1 не является чётным числом.
Чётность нуля
Ноль чётное число, так как оно делится на два без остатка: 0 ÷ 2 = 0
Нечётные числа
Нечетным является целое число, которое не делится на 2 без остатка.
Все многозначные числа, оканчивающиеся на 1,3,5,7 или 9, являются нечётными числами:
Пример
Для примера рассмотрим число 67. Так как оно заканчивается цифрой 7 (нечётной), уже можно утверждать, что оно нечётное. Для пущей уверенности разделим 67 на два:
67 ÷ 2 = 33.5, то есть 33 и остаток 1 (67 = 33 ⋅ 2 + 1)
Окончательно делаем вывод, что число 67 является нечётным числом.
Сколько чётных и нечётных чисел в ряду
Сколько чётных и нечётных чисел находится в ряду между n и m?
Если n и m разные по чётности
Если n и m разные по чётности числа, то есть одно из них четное, а второе нечётное, то количество чётных и нечётных чисел в ряду одинаковое:
Пример
Возьмём ряд чисел между n = 22 и m = 31:
22, 23, 24, 25, 26, 27, 28, 29, 30, 31
Определим количество чётных и нечётных чисел в этом ряду.
Так как 22 и 31 являются числами разной чётности делаем вывод, что чётных и нечётных чисел в данном ряду поровну:
5 чётных и 5 нечётных
| 22 | 24 | 26 | 28 | 30 |
| 23 | 25 | 27 | 29 | 31 |
Если n и m чётные
Если n и m чётные числа, то чётных чисел в ряду будет на одно больше, чем нечётных:
Пример
Возьмём ряд чисел между n = 10 и m = 20:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Определим количество чётных и нечётных чисел в этом ряду.
6 чётных и 5 нечётных
| 10 | 12 | 14 | 16 | 18 | 20 |
| 11 | 13 | 15 | 17 | 19 |
Если n и m нечётные
Если n и m нечётные числа, то чётных чисел в ряду будет на одно меньше, чем нечётных:
Пример
Возьмём ряд чисел между n = 11 и m = 19:
11, 12, 13, 14, 15, 16, 17, 18, 19
Определим количество чётных и нечётных чисел в этом ряду.
Что такое нечетные числа и как их узнать?
Прежде чем говорить про четные и нечетные числа, стоит уяснить несколько моментов о том, какие вообще группы чисел бывают. Это необходимо для того, чтобы не пытаться выяснять четность дроби.
С каких чисел начинается изучение в основной школе?
Первыми идут натуральные. Они также сначала появились исторически. Человечеству было необходимо подсчитывать предметы. Причем при счете ноль не используется, поэтому он не входит в группу натуральных чисел. Здесь все целые, которые больше единицы.
Именно для них впервые дается определение четности. Чтобы понять, какое число нечетное, нужно запомнить признак четного. Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.
Какие числа идут дальше?
Целые. В их множество входит уже ноль и все отрицательные числа. Цепочка натуральных чисел была ограничена слева, а вправо продолжалась бесконечно. С целыми оказывается бесконечное количество чисел и слева от нуля.
В этот момент немного меняется определение четности. Оно теперь должно делиться на два без остатка. Значит, нечетные числа при делении на два дают ответ с остатком.
Причем даже вводится общая запись: для четных — 2n, нечетные — (2n+1). Если для натуральных не существует только максимального четного или нечетного, то у целых нет и минимального.
А что потом?
Кстати, для них не вводится понятие четности. Поэтому нечетные числа, записанные в виде дроби, не существуют вовсе.
Какие результаты дают действия с четными и нечетными числами?
Их можно рассмотреть в порядке усложнения арифметического действия. Тогда первым и вторым пойдут сложение и вычитание. Неважно, какое из них выполняется, ответ будет зависеть только от начальной пары чисел. К примеру, если исходные числа четные, то результат действия будет делиться на два. Такой же итог будет, если стоит разность или сумма нечетных чисел. Чтобы получить нечетное число, придется складывать или вычитать четное с нечетным.
Это легко можно проверить, используя их общую запись. Например, сложение двух четных чисел: 2n+2n = 4n = 2*2n. Здесь 2n — четное число, которое еще умножается на два. Значит, оно точно будет делиться нацело на двойку. То есть ответ — четный.
При сложении четного с нечетным имеем такую запись: 2n + (2n + 1) = 4n + 1. Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.
Третье действие — умножение. При его выполнении всегда будет четный ответ, если есть хотя бы один множитель четный. В ситуации, когда перемножаются два нечетных числа, результатом окажется нечетное.
Для иллюстрации последнего потребуется сделать такую запись: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Опять первое слагаемое представляет собой четное число, а единица сделает его нечетным.
Если делится нечетное число на четное, то ответ оказывается всегда дробным. Значит, его четность не определяется.
Когда в делении участвуют нечетные числа, то результатом также может оказаться дробь. Но если ответ целый, то он обязательно будет нечетным.
При делении четного на нечетное, как в предыдущей ситуации, возможно два варианта: дробь или целое число. Во втором случае оно всегда будет четным.
Четные и нечетные числа
Четные и нечетные числа: что, как, зачем, почему
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это число, которое делится на 2.
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это число, которое не делится на 2.
5 не делится на 2 без остатка — значит, 5 это нечетное число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.
Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.
Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.
Свойства четных и нечетных чисел
Четные и нечетные числа чередуются друг с другом
1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.
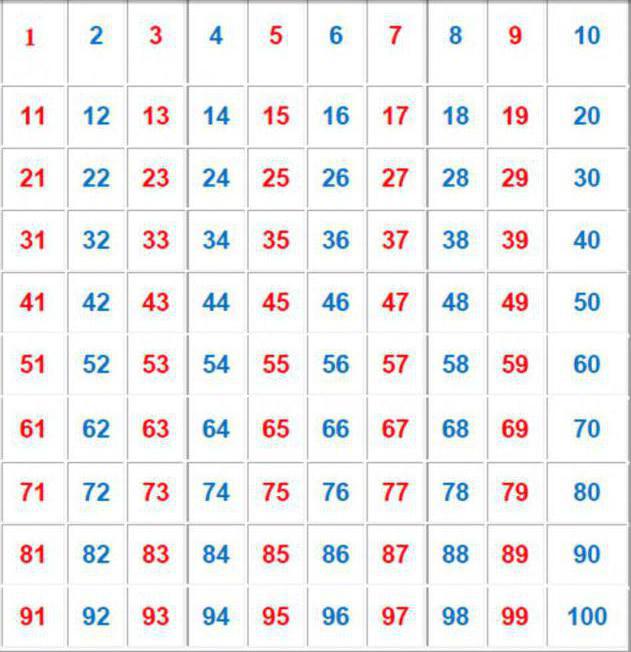
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Задачи для практики
Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 11 | 19 |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)
Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| ☆ | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
126 : 2 = 63
Четное или нечетное число
Хотите начать заниматься математикой прямо сейчас
Уже в дошкольном возрасте ребята узнают, что бывают четные и нечетные числа. Определить абстрактно, четное число или нечетное, бывает непросто. Зато каждому понятно, получится ли некоторое количество разделить на двоих без остатка, или нет. Объяснить ребенку четные и нечетные числа помогут занимательные упражнения.
Что такое четные и нечетные числа
Таблица четных и нечетных чисел
Чтобы быстро определить, четным или нечетным является число, можно воспользоваться таблицей до 100. В ней четные и нечетные числа будут чередоваться. В нашей таблице выделены четные числа.
Определяем, четный или нечетный
Сначала расскажите ребенку, что такое четные и нечетные числа.
Проиллюстрируйте это на примерах – раскладывайте перед ребенком разное количество карандашей и попытайтесь разделить на две равные части. Если так получилось сделать, то число карандашей является четным. Если остался лишний карандаш – число нечетное.
Запоминание приходит с практикой. Вначале пусть ребенок продолжает ряды четных или нечетных чисел, начиная с указанного вами числа. В этом упражнении пригодится навык счета через один. Следующим этапом предлагайте определить четность или нечетность любого числа. Поиграйте в игру: вы загадываете число в небольшом диапазоне и сообщаете, что оно находится между 4 и 7. А ребенок, используя вопрос: «Это четное или нечетное число?», пытается угадать задуманное число. Если ребенок угадал, то следующий вопрос задает он.
Правила сложения четных и нечетных чисел
Даже если ребенок не умеет складывать числа в уме, он может запомнить несколько простых правил:
Какое число 0 – четное или нечетное?
Ноль – это четное число.
Некоторые взрослые до сих пор затрудняются правильно ответить на этот вопрос. Как же это доступно объяснить детям?
Во-первых, чтобы определить четность или нечетность, нужно вспомнить какие числа называются четными – те, которые делятся на 2 без остатка. Ноль делится на 2 без остатка. Значит, ноль – четное число.
Во-вторых, мы уже знаем, что четные и нечетные числа чередуются. После ноля стоит нечетное число 1. Значит ноль – четное число.
Также поможет запомнить четность ноля тот факт, что все числа, которые заканчиваются на 0 – четные. Значит и ноль тоже четное число.
Игры с четными и нечетными числами
Для того чтобы знания о четных и нечетных числах закрепились у малыша в памяти, регулярно используйте эти понятия в игре.
Например, в игре в магазин вы можете “печатать” для товаров ценники только с нечетными числами, выдумывая двузначные или трёхзначные числа из головы. Остается только вспомнить, на какие цифры должны оканчиваться эти числа.
Напомнить знания о четных и нечетных поможет обычное русское лото. Когда вы с ребенком заполняете фишками карточки лото, проговаривайте вслух, является ли число четным.
Айкьюша поможет легко и в игровой форме познакомиться с математикой для детей 6-7 лет. Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.
Материалы для самостоятельных занятий по математике с дошкольником
| Предложите ребенку раскрасить предметы с четными числами в зеленый цвет, а с нечетными – в красный. | Распечатайте картинку и предложите ребенку продолжить последовательность четных и нечетных чисел, начиная с шеи жирафа. |
 |  |
Превратите изучение четных и нечетных чисел в увлекательное занятие – и ребенок без труда освоит эту непростую тему!
JavaScript | Как проверить на чётное?
Как узнать, является ли число чётным?
Для начала вспомним какое число называют чётным.
Чётное число — это целое число, которое делится на 2 без остатка.
Чтобы проверить число на чётное, мы можем воспользоваться одним из мультипликативных операторов — % (знак процента). Этот оператор возвращает остаток от деления. Если число будет чётным, тогда при делении его на 2 мы будем получать 0 (ноль). То есть остатка от деления на 2 не будет.
Мультипликативное выражение будет выглядеть так:
Теперь мы можем протестировать на реальных примерах наше условие:
true означает то, что левое число является чётным
false означает то, что левое число не является чётным

Функция проверки числа на ЧЁТНОЕ
Проверку этого условия можно обернуть в функцию:
Пример работы функции:
Скрин из консоли браузера:

На английском языке
«even» — чётное
«odd» — нечётное
Другой способ проверить на чётное
В этом случае проверка на чётное будет выглядеть так: