как узнать номер перестановки

Как узнать номер перестановки

Добрый день. Возник вопрос: можно ли узнать номер перестановки (если их все выписать в лексикографическом порядке) за O(N)?

Я спрашивал о существовании решения за O(N).

Для маленьких N можно предподсчитать табличку размера 2 N и дальше находить номер за O(N) на запрос.

Спасибо большое, согласен.

Я умею табличку 2 N ·N :
2 N даёт маска уже использованных чисел,
N — для какого числа мы хотим узнать позицию.

Поясните, пожалуйста, подробнее.

Все, сам додумал до конца. Спасибо.

(Нынче даже массив не очень нужен, операция popcount стала быстрой.)

Источник

По перестановке определить его номер в лексикографическом перечислении всех перестановок множества

По перестановке определить его номер в лексикографическом перечислении всех перестановок множества <1,2,…,n>.
Формат входных данных:
Входной файл содержит в первой строке одно число n – количество элементов в перестановке, во второй – перестановку.
Формат выходных данных:
Входной файл должен содержать номер заданной перестановки в лексикографическом перечислении всех перестановок.
Примеры:
INPUT.TXT
8
8 3 4 5 6 1 7 2

Пример похожей задачи

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Программа генерации всех сочетаний n-элементного множества в лексикографическом порядке
Доброе утро. У меня есть массив a:array of integer; Массив может быт больше. (a:array of.

По размещению найдите его номер в лексикографическом порядке
По размещению найдите его номер в лексикографическом порядке Формат входных данных В первой.

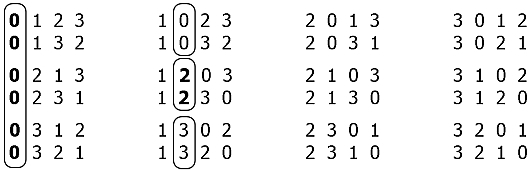
Генерация всех перестановок элементов множества
Где можно взять алгоритм генерации всех перестановок элемента множества? Например, если M =

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Генерация всех перестановок n элементного множества
с++ 1) Напечатать все перестановки чисел от 1 до n используя рекурсивный алгоритм пример 123.

Генерация всех перестановок заданного множества
Никак не могу понять в чем проблема, задача состояла в генерации всех перестановок заданного.

Вывод всех перестановок k элементов из множества N имеющихся
Всем привет нужен алгоритм (любой на словах или кодом) выводящий все перестановки k элементов (не.

Генерация всех перестановок N-элементного множества в лексмкографическом порядке
Реализовать программу генерации всех перестановок N-элементного множества в лексикографическом.

По исходной перестановке вывести все циклы, которые в ней есть, в лексикографическом порядке
Перестановкой π порядка n называется последовательность из n попарно различных целых положительных.

Источник

Как узнать номер перестановки

пятница, 11 февраля 2011 г.

Часть 4. Генерация перестановки по номеру и получение номера по перестановке

Теория: Окулов. Программирование в алгоритмах. 2004.

Рассмотрим две задачи:
1) Генерация перестановки по номеру
2) Получение номера по перестановке

Генерация перестановок происходит в лексикографическом порядке. Нумерация перестановок начинается с единицы.

Практика:
Обе задачи реализуем на основе problem Перестановка по номеру.

1) Генерация перестановки по номеру
Вся необходимая теория довольно популярно изложена в книге Окулова. Остановлюсь на некоторых моментах. Перестановку будем последовательно получать слева направо. Сначала мы имеем N пустых позиций перестановки. Если выписать в столбец все перестановки в лексикографическом порядке то увидим, что их можно разбить на N групп размерностью по (N-1)! каждая. Зная номер перестановки можно без проблем определить в какую группу она попадет. Номер группы и уже полученное начало перестановки однозначно определяют текущий элемент перестановки.
Общую логику передает функция permutation_by_num:

2) Получение номера по перестановке
Для решения этой задачи в первую очередь нужно понять принцип решения первой задачи, а потом проделать обратные манипуляции.
Мне не удалось найти problem, которая в чистом виде решает поставленную задачу. Но у нас есть problem Перестановка по номеру, на основе которой можно проверить правильность решения этой задачи.

Источник

Анализ алгоритма

Пусть m₁ m₂… m_n – входная перестановка. Обозначим через d_i количество таких пар ( i, j), что i j и m[ i] > m[ j] (элементы m[ i] и m[ j] образуют инверсию). То есть d_i равно количеству таких чисел, которые стоят правее от i-ой позиции и меньше m[ i].

Тогда номер перестановки в лексикографическом порядке определяется по формуле:

Для перестановки (2, 1, 3) массив d = (1, 0, 0). Номер перестановки равен 1 * 2! + 1 = 3.

Для перестановки (1, 4, 3, 2) массив d = (0, 2, 1, 0). Номер перестановки равен 0 * 3! + 2 * 2! + 1 * 1! + 1 = 6.

Для перестановки (3, 2, 1, 4) массив d = (2, 1, 0, 0). Номер перестановки равен 2 * 3! + 1 * 2! + 0 * 1! + 1 = 15.

Для лексикографически наименьшей перестановки (1, 2, …, n) массив d = (0, 0, …, 0). Ее номер равен 1, так как все слагаемые кроме последнего равны нулю.

Для лексикографически наибольшей перестановки ( n, n – 1, n – 2, …, 1) массив d = ( n – 1, n – 2, n – 3, …, 0). Ее номер равен ( n – 1) * ( n – 1)! + ( n – 2) * ( n – 2)! + … + 1 * 1! + 1 = n! Эту формулу можно доказать методом математической индукции:

База индукции. 1 = 1!.

Реализация алгоритма

Заполняем массив факториалов чисел.

for (inv = 0, j = i + 1; j

Добавляем к результату значение d _i * ( n – i )!

Источник

Алгоритм создания списка всех перестановок или размещений

Сразу оговорюсь, эта статья тематически похожа на опубликованную около года назад автором SemenovVV «Нерекурсивный алгоритм генерации перестановок», но подход тут, на мой взгляд, принципиально иной.

Я столкнулся с необходимостью составления списка всех перестановок из n элементов. Для n = 4 или даже 5, задача решается вручную в считанные минуты, но для 6! = 720 и выше исписывать страницы мне уже было лень – нужна была автоматизация. Я был уверен, что этот «велосипед» уже изобретён многократно и в различных вариациях, но было интересно разобраться самостоятельно – поэтому, намеренно не заглядывая в профильную литературу, я засел за создание алгоритма.

Первую же версию кода с рекурсией я отбросил как слишком тривиальную и ресурсоёмкую. Далее, сделав «финт ушами», разработал не очень эффективный алгоритм, перебирающий заведомо большее количество вариантов и отсеивающий лишь подходящие из них. Он работал, но мне хотелось чего-то элегантного – и, начав с чистого листа, я принялся искать закономерности в лексикографическом порядке перестановок для малых значений n. В итоге получился аккуратный код, который с минимальной «обвязкой» можно на Python представить строк в 10 (см. ниже). Более того, этот подход работает не только для перестановок, но и для размещений n элементов по m позициям (в случае когда, n≥m).
Если взглянуть на перечень всех перестановок для 4 по 4, то заметна определённая структура:

Весь массив перестановок (4! = 24) можно разбить на группы из (n-1)! = 3! – шести перестановок, а каждую группу в свою очередь разбить на (n-1-1)! = 2! –две комбинации и так далее. В рассмотренном случае, когда для n = 4, на этом – всё.

Итак, с точки зрения лексикографии этот набор перестановок можно представить себе как возрастающий ряд: так сказать, 0123

Источник