как узнать нормальное ли распределение
Тестирование данных на нормальность часто является первым этапом их анализа, так как большое количество статистических методов исходит из предположения нормальности распределения изучаемых данных.
Например, пусть необходимо проверить гипотезу о равенстве средних значений в двух независимых выборках. Для этой цели подходит критерий Стьюдента. Но применение критерия Стьюдента обосновано, только если данные подчиняются нормальному распределению. Поэтому перед применением критерия необходимо проверить гипотезу о нормальности исходных данных. Или проверка остатков линейной регрессии на нормальность — позволяет проверить, соответствует ли применяемая модель регрессии исходным данным.
Нормальное распределение естественным образом возникает практически везде, где речь идёт об измерении с ошибками. Более того, в силу центральной предельной теоремы, распределение многих выборочных величин (например, выборочного среднего) при достаточно больших объёмах выборки хорошо аппроксимируется нормальным распределением вне зависимости от того, какое распределение было у выборки исходно. В связи с этим становится понятным, почему проверке распределения на нормальность стоит уделить особое внимание. В дальнейшем речь пойдёт о так называемых критериях согласия (goodness-of-fit tests). Проверяться будет не просто факт согласия с нормальным распределением с определёнными фиксированными значениями параметров, а несколько более общий факт принадлежности распределения к семейству нормальных распределений со всевозможными значениями параметров.
Проверку выборки на нормальность можно производить несколькими путями. Для начала можно вспомнить, какой вид у графика нормального распределения (гистограмма, график плотности и т.п.), как в нормальном распределении соотносятся среднее, мода, медиана, какими должны быть асимметрия и эксцесс, выполняется ли «правило 3-х сигм». Про всё это мы писали в статье про нормальное распределение. Вот с помощью такой описательной статистики можно оценить выборку на нормальность (обычно приемлемо отклонение на порядок ошибки рассчитываемого параметра). Вторая группа методов — критерии нормальности.
Критерии нормальности
Список критериев нормальности:
Подробно эти критерии с формулами и таблицами можно посмотреть здесь.
Проверка на нормальность в R (источник)
Самый простой графический способ проверки характера распределения данных — построение гистограммы (с помощью функции hist() — это сделать несложно). Если гистограмма имеет колоколообразный симметричный вид, можно сделать заключение о том, что анализируемая переменная имеет примерно нормальное распределение. Однако при интерпретации гистограмм следует соблюдать осторожность, поскольку их внешний вид может сильно зависеть как от числа наблюдений, так и от шага, выбранного для разбиения данных на классы.
Другим очень часто используемым графическим способом проверки характера распределения данных является построение т.н. графиков квантилей (Q-Q plots, Quantile-Quantile plots). На таких графиках изображаются квантили двух распределений — эмпирического (т.е. построенного по анализируемым данным) и теоретически ожидаемого стандартного нормального распределения. При нормальном распределении проверяемой переменной точки на графике квантилей должны выстраиваться в прямую линию, исходящую под улом 45 градусов из левого нижнего угла графика. Графики квантилей особенно полезны при работе с небольшими по размеру совокупностями, для которых невозможно построить гистограммы, принимающие какую-либо выраженную форму.
В R для построения графиков квантилей можно использовать базовую функцию qqnorm(), которая в качестве основного аргумента принимает вектор со значениями анализируемой переменной.
Следует отметить, что интерпретация графиков квантилей при работе с небольшими выборками, происходящими из нормально распределенных генеральных совокупностей, требует определенного навыка. Дело в том, что при небольшом числе наблюдений точки на графике квантилей могут не всегда образовывать четко выраженную прямую линию. В качестве иллюстрации этого утверждения на следующем рисунке приведены графики квантилей для 5 случайным образом сгенерированных нормально распределенных выборок по 20 наблюдений каждая (если использованный в примере пакет DAAG у Вас не установлен, выполните команду install.packages(«DAAG»)):
library(DAAG)
qreference(m = 20, seed = 145, nrep = 5, nrows = 1)
Фигура, в которую выстраиваются точки на некоторых графиках далека от прямой линии. Причина данного эффекта — в небольшом объеме наблюдений.
Тесты проверки на нормальность в R
Существует целый ряд статистических тестов, специально разработанных для проверки нормальности распределения данных. В общем виде проверяемую при помощи этих тестов нулевую гипотезу можно сформулировать так: «Анализируемая выборка происходит из генеральной совокупности, имеющей нормальное распределение». Если получаемая при помощи того или иного теста вероятность ошибки Р оказывается меньше некоторого заранее принятого уровня значимости (например, 0.05), нулевая гипотеза отклоняется.
В R реализованы практически все имеющиеся тесты на нормальность — либо в виде стандарных функций, либо в виде функций, входящих в состав отдельных пакетов. Примером базовой функции является shapiro.test(), при помощи которой можно выполнить широко используемый тест Шапиро-Уилка:
Основные классические критерии проверки на нормальность собраны в пакете nortest. Пакет можно установить с CRAN при помощи вызова функции install.packages():
Подключить установленный пакет можно при помощи функции library():
Может возникнуть вопрос: «А зачем столько много разных критериев для проверки одного факта? Нельзя ли выбрать наилучший и всегда его использовать?». Ответ на этот вопрос не утешителен: «В общем случае, к сожалению, нельзя».
Проверка гипотезы о виде распределения
Характеристики распределений
Равномерное распределение
Графическое представление  Функция плотности равномерного распределения 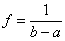 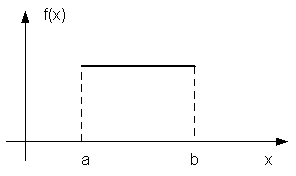 | Математическое ожидание: M[X] = (a+b)/2 Дисперсия:  |
Нормальное распределение
Графическое представление 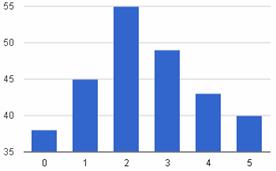 Плотность распределения 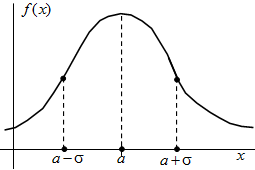 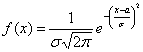 | Математическое ожидание: M[X]=a 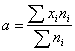 Дисперсия: D[X] = σ 2 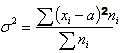 Запись Х |
N( a ; σ) означает, что случайная величина Х распределена по нормальному закону с параметрами a и σ.
Показательное распределение
Графическое представление  Плотность распределения 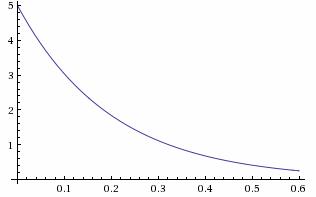 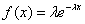 | Математическое ожидание: M[X] = 1/λ Дисперсия: D[X] = 1/λ 2 |
Распределение Пуассона
Биномиальное распределение
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
Пример 1. Нормальным или гауссовым распределением называется непрерывное распределение, плотность которого имеет вид
φ(x)– функция Гаусса (таблица),
Параметры a и σ имеют смысл математического ожидания и среднего квадратичного отклонения.
2. Справедливы формулы:
Ф(x)– интеграл вероятностей, таблица.
Обратим внимание, что Ф(-x)=–Ф(x), Ф(x)=0.5 при x>5.
3. Правило трех сигм: P(|X-a|>3ε)=0.0027 – т.е. вероятность отклонения нормально распределенной величины от математического ожидания более чем на 3σ практически равна нулю.
Главная особенность, выделяющая нормальный закон среди других законов распределения, состоит в том, что он является предельным, к которому приближаются другие законы при весьма часто встречающихся условиях.
Выбираем в качестве начала интервала 6.07, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 6.16
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
Таким образом, что 25% единиц совокупности будут меньше по величине 5.86
Q2 совпадает с медианой, Q2 = 6.1
Остальные 25% превосходят 6.26
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
Таким образом, что 10% единиц совокупности будут меньше по величине 5.76
Каждое значение ряда отличается от другого не более, чем на 0.22
Дисперсия
Среднее квадратическое отклонение
Каждое значение ряда отличается от среднего значения 6.08 не более, чем на 0.25
Коэффициент вариации
Проверка распределения на нормальность в EXCEL
history 22 ноября 2016 г.
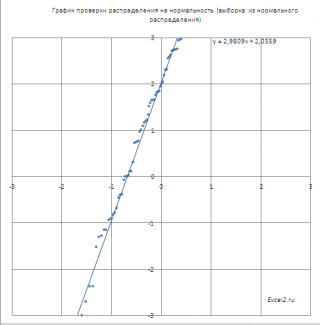
Построение графика проверки распределения на нормальность ( Normal Probability Plot ) является графическим методом определения соответствия значений выборки нормальному распределению.
Из-за наличия неустранимой статистической ошибки выборки, присущей случайной величине, невозможно однозначно ответить на вопрос «Взята ли данная выборка из нормального распределения или нет». Поэтому, рассмотренный графический метод, скорее, дает ответ на вопрос «Разумно ли предположение, что оцениваемая выборка взята из нормального распределения »?
Рассмотрим алгоритм построения графика проверки распределения на нормальность ( Normal Probability Plot ) :
Если значения выборки взяты из нормального распределения (μ не обязательно равно 0, σ не обязательно равно 1), то угол наклона кривой даст оценку стандартного отклонения σ, а ордината точки пересечения оси Y – оценку среднего значения μ.
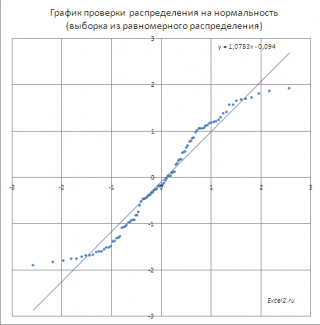
Интересно посмотреть, как будут выглядеть на диаграмме данные, полученные из выборок из других распределений (не из нормального ). В файле примера на листе Равномерное приведен график, построенный на основе выборки из непрерывного равномерного распределения.
Очевидно, что значения выборки совсем не ложатся на прямую линию и предположение о нормальности выборки должно быть отвергнуто.
Как определить, является ли распределение нормальным?
Если установлено, что исследуемые значения имеют количественный характер, следует проверить выборку на нормальность распределения. Это можно сделать несколькими способами.
Первый способ проверки выборки на нормальность распределения
Прежде всего, нужно вычислить показатели асимметрии и эксцесса, используя программу Excel, имеющуюся практически на всех компьютерах. Для этого в таблицу программы следует поместить результаты измерений. Пусть это будет ряд значений, полученных на выборке из 25 объектов: 9 10 10 10 11 11 11 11 12 12 12 12 12 12 12 13 13 13 13 14 14 15 15 16 17
По схожему алгоритму вычисляем величину показателя эксцесса характеризующего подъем или снижение вершины распределения, то есть – отклонения по оси ординат. Для того, чтобы произвести расчет данного показателя, следует выбрать пункт «эксцесс». В окне «Аргументы функций» получим его значение – 0,116.
При наличии статистических таблиц критических значений асимметрии и эксцесса (в данном учебном пособии это таблицы 9 и 10) вычисленные значения сравниваются с табличными. Если оба (!) показателя окажутся меньше табличных величин, то распределение может считаться нормальным.
Для нашего примера табличное значение показателя асимметрии находим на пересечении строки n = 25 и колонки р ≤ 0,01 (предположим, что мы анализируем результаты достаточно важных экспериментов и считаем, что вероятность ошибки статистического заключения не должна превышать 1%). Это число составляет 1,061. Так как вычисленное значение показателя асимметрии 0,579 оказывается гораздо меньше табличной величины 1,061, можно сделать заключение, что отклонение вершины распределения по оси абсцисс не столь значительно, чтобы отказаться от применения параметрических методов.
В таблице 10 находим критическое значение показателя эксцесса. Для n = 26 (так как в таблице отсутствует строка для n = 25, переходим к ближайшей строке) и
р ≤ 0,01 оно составляет 0,869. И снова фактическое значение показателя 0,116 оказывается меньше табличного 0, 869. Отсюда следует, что отклонение вершины распределения по оси ординат также несущественно и его можно считать нормальным. То, что оба показателя оказались меньше критических табличных величин, дает основание для последующего применения параметрических критериев.
Второй способ проверки выборки на нормальность распределения
При отсутствии таблиц критических значений асимметрии и эксцесса следует произвести расчеты не только этих показателей, но и их выборочных ошибок.
Ошибка показателя асимметрии производится по формуле:
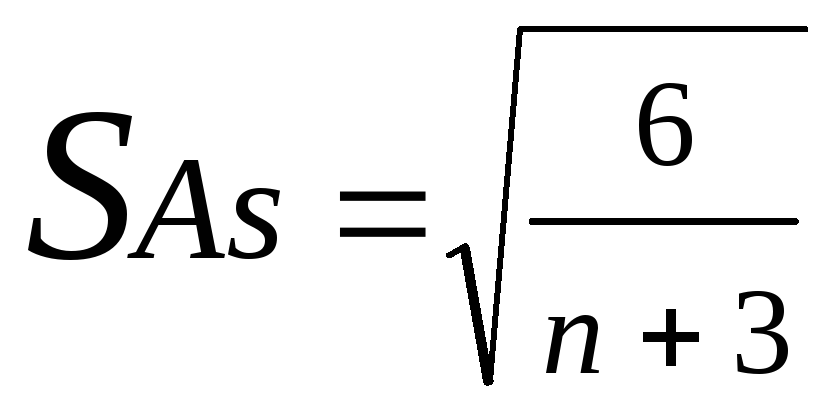
Выборочная ошибка эксцесса рассчитывается по другой формуле:
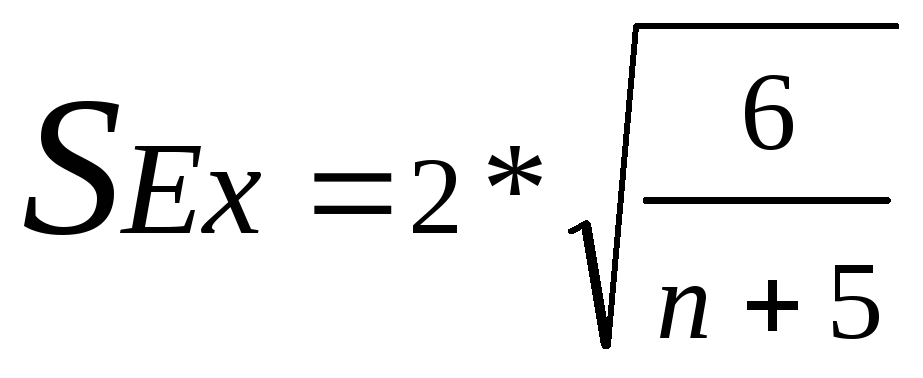
Далее следует разделить показатели асимметрии и эксцесса на их ошибки.
Частное от деления показателей асимметрии и эксцесса на их ошибки определяется как tф (фактическое значение) и сравнивается с tт,табличное значение), взятым из таблицы Стьюдента (таблица 6), при соответствующем уровне значимости и числе степеней свободы. Если фактическое значение критерия Стьюдента окажется меньше табличного, распределение признается нормальным, и, наоборот, если фактическое значение окажется больше табличного, следует сделать вывод о несоответствии распределения нормальному закону.
Для показателя асимметрии получаем следующее значение t-критерия:
Число степеней свободы (df), определяющее строку в таблице Стьюдента, находим как n-1. Следовательно, df = 25-1=24. Уровень значимости (вероятность ошибки статистического заключения), определяющий колонку в таблице Стьюдента, оставляем 1%. На пересечении строки df =24 и колонки р ≤ 0,01 находим табличное значение критерия tт = 2,80. Так как tф (1,25) оказывается гораздо меньше чем tт (2,80), можно заключить, что и второй способ проверки указывает на незначительность асимметрии кривой распределения.
Фактическое значения t-критерия для показателя эксцесса рассчитываем по формуле 
Третий способ проверки выборки на нормальность распределения
Проще всего задача решается, если имеется компьютер с установленной на ней программой Statistica. После ввода данных в таблицу вызывается стартовая панель модуля Основные статистики и таблицы (Basic Statistics/Tables). В средней части окна Descriptive Statistics (Описательные статистики) слева находится блок проверки распределений (Distribution). Чтобы проверить, относятся ли показатели выбранной переменной к распределяемым по нормальному закону, нужно поставить галочку в окне возле пункта K-S and Lilliefors test for normality (Критерий Колмогорова-Смирнова и Лилиефорса для нормальности) и нажать на кнопку Histograms (гистограммы). В появившемся окне приводятся гистограмма распределения значений переменной и наложенная на нее кривая нормального распределения, сопоставление которых позволяет визуально оценить характер распределения.
В верхней части окна указывается достоверность отличия проверяемого распределения от нормального, характеризуемая уровнем значимости р (вероятность неправильного отвержения гипотезы, если она верна). Если уровень значимости р 0,05, как на рисунке, то наблюдаемая величина распределена нормально. Зная вид распределения, в дальнейшей обработке можно применить оптимальные статистические методы.
Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z