как узнать объем куба формула

Объемы фигур. Объем куба.

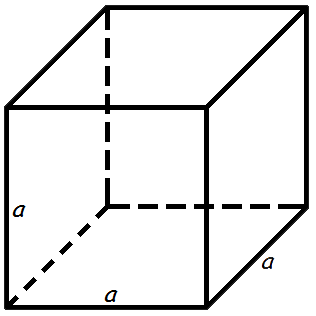
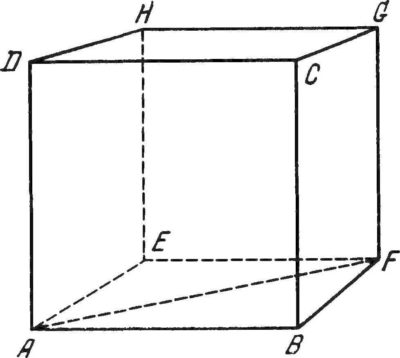
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна

где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Метод 1 из 3: Возведение в куб ребра куба

вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.

Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.

Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.

и, таким образом, вы вычислите объем куба.

Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на

ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,

другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и

равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.

В нашем примере объем куба равен:

характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические

В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических

Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих

Метод 2 из 3: Вычисление объема по площади поверхности

можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите

ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем

возведите длину ребра куба в третью степень и вычислите объем куба.

где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так

как у куба 6 равных граней).

одной грани и получите длину ребра куба.

В нашем примере, √8,33 = 2,89 см.

Метод 3 из 3: Вычисление объема по диагонали

если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив

Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба

которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен

сумме квадратов катетов (в нашем случае ребер), то есть:

дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.

Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае

диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –

это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть

Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.

Источник

Объем куба

Свойства

Куб представляет собой прямоугольный параллелепипед, у которого все ребра равны между собой. Поэтому объем куба вычисляется не просто произведением всех трех его параметров, а возведением ребра куба в третью степень. Поэтому чтобы вычислить ребро куба через объем необходимо извлечь из последнего кубический корень. a=∛V

Площадь грани куба или одной его стороны равна площади квадрата, стороной которого является ребро куба, поэтому кубический корень из объема необходимо возвести во вторую степень. S=∛(V^2 )

Площадь боковой и полной поверхности куба состоят из четырех и шести таких граней соответственно, поэтому их формулы являются аналогией предыдущей с добавлением необходимых коэффициентов. S_(б.п.)=4∛(V^2 ) S_(п.п.)=6∛(V^2 )

Периметр куба равен сумме двенадцати его ребер, равных между собой, поэтому зная, что каждое ребро представлено в виде кубического корня из объема, необходимо умножить его на двенадцать. P=12a=12∛V

Чтобы вычислить диагональ грани куба, нужно вернуться к формуле диагонали квадрата, которым представлены грани. Согласно ей, чтобы найти диагональ, нужно умножить корень из двух на сторону квадрата – ребро куба в данном случае, или кубический корень из объема. d=a√2=∛V √2

Найти диагональ самого куба немного сложнее. Для этого три вершины – диагонали и прилегающего к ней бокового ребра – соединяются в прямоугольный треугольник через диагональ основания, и по теореме Пифагора выводится формула диагонали куба. (рис.2.1) a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3=∛V √3

Чтобы найти радиус сферы, вписанной в куб, через объем, нужно разделить его кубический корень, представляющий собой ребро куба, на два. (рис. 2.2) r=a/2=∛V/2

Радиус сферы, описанной вокруг куба, равен половине диагонали куба, поэтому подставив вместо диагонали необходимую формулу через объем, получим следующее выражение: (рис.2.3) R=D/2=(∛V √3)/2

Источник

Формулы объема геометрических фигур

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

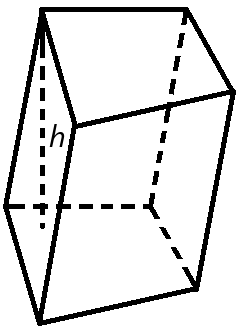
Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

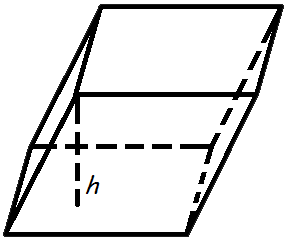
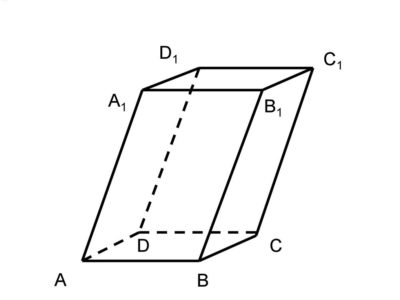
Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

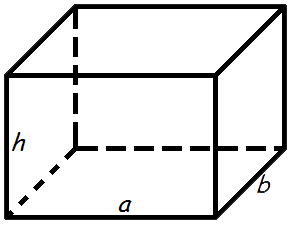
Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

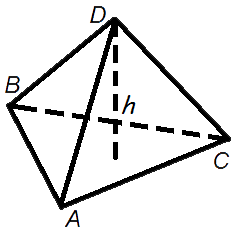
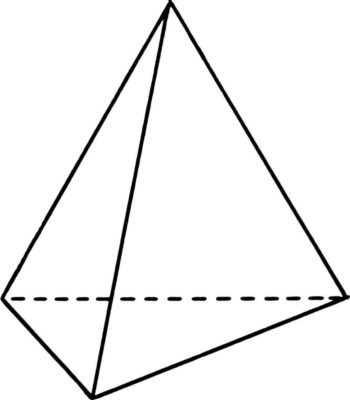
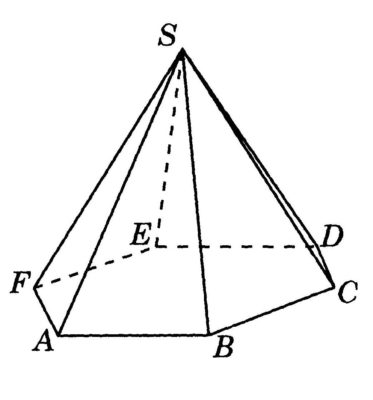
Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

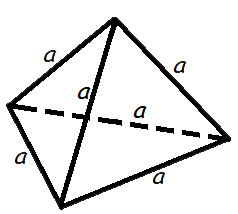
Объем правильного тетраэдра

Формула объема правильного тетраэдра:

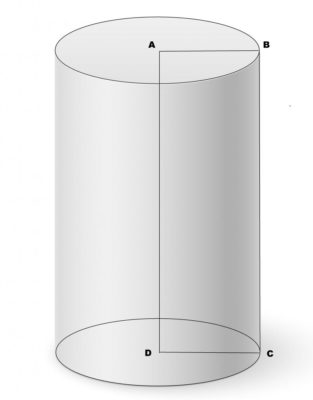
Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Формула объема.

Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.

Объемы геометрических фигур.

Параллелепипед.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Цилиндр.

Объем цилиндра равен произведению площади основания на высоту.

Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

Пирамида.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.

Усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁(abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию.

V = 1/3 πh (R 2 + Rr + r 2 )

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Призма.

Объем призмы равен произведению площади основания призмы, на высоту.

Сектор шара.

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.

Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.

Источник

Как найти объём геометрических фигур

Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м 3 ).

Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.

Содержание:

Как найти объем трехмерных объектов

Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.

Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м 3 /1000000 = 0,004256 м 3

Как найти объем для фигур цилиндрической формы

Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.

Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.

Как рассчитать объем треугольной пирамиды

Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.

Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.

В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.

Как посчитать объем куба

Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.

Как найти объем прямоугольного параллелепипеда

Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:

Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см 3

Советы по измерению:

Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.

Как найти объем цилиндра

Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:

Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:

3,14 * 2 см 2 * 5 см = 62.831853071796 = 63см 3

Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.

Как найти объем пирамиды

фото 6 — посчитать объём

Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:

Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:

V = 3 * 2 = 2 см 3 ‒ это и будет являться объемом искомой геометрической фигуры.

Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.

Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.

Источник

• ← как узнать объем куба метра
• как узнать объем кузова в кубах →

Фигура	Формула	Чертеж