как узнать объем прямоугольника в м3
Онлайн калькулятор. Объем прямоугольного параллелепипеда.
Используя этот онлайн калькулятор для вычисления объема прямоугольного параллелепипеда, вы сможете очень просто и быстро найти объем прямоугольного параллелепипеда, зная значения его длины, ширины и высоты.
Воспользовавшись онлайн калькулятором для вычисления объема прямоугольного параллелепипеда, вы получите детальное решение вашего примера, которое позволит понять алгоритм решения задач и закрепить пройденный материал.
Найти объем прямоугольного параллелепипеда
| a | = |
| b | = |
| h | = |
Ввод данных в калькулятор для вычисления объема прямоугольного параллелепипеда
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины, конвертером единиц площади и конвертером единиц объема.
Дополнительные возможности калькулятора для вычисления объема прямоугольного параллелепипеда
Теория. Объем прямоугольного параллелепипеда.
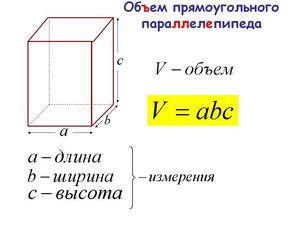
Формула для вычисления объема прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Как вычислить объем прямоугольника
Чтобы вычислить объем прямоугольного параллелепипеда, перемножьте между собой его длину, ширину и высоту (толщину). То есть воспользуйтесь формулой:
где: a, b и с – длина, ширина и высота параллелепипеда (соответственно), а V – его объем.
Все длины сторон предварительно приведите к одной единице измерения, тогда и объем параллелепипеда получится в соответствующих «кубических» единицах.
Какова будет емкость бака для воды, имеющего размеры:
длина – 2 метра;
ширина – 1 метр 50 сантиметров;
высота – 200 сантиметров.
1. Приводим длины сторон к метрам: 2; 1,5; 2.
2. Перемножаем полученные числа: 2 * 1,5 * 2 = 6 (кубических метров).
Если речь в задаче идет все-таки о прямоугольнике, то наверняка требуется вычислить его площадь. Для этого просто умножьте длину прямоугольника на его ширину. То есть примените формулу:
где:
a и b – длины сторон прямоугольника,
S – площадь прямоугольника.
Используйте эту же формулу, если в задаче рассматривается грань прямоугольного параллелепипеда – согласно определения, она также имеет форму прямоугольника.
Объем куба составляет 27 м³. Чему равна площадь прямоугольника, образуемого гранью куба?
Длина ребра куба (являющегося также и прямоугольным параллелепипедом) равняется корню кубическому из его объема, т.е. 3 м. Следовательно, площадь его грани (представляющей из себя квадрат) будет равна 3 * 3 = 9 м².
Формулы вычисления объёма прямоугольника и параллелепипеда
Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.
Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.
Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:
Вычисление объема прямоугольного параллелепипеда
Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.
Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.
Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.
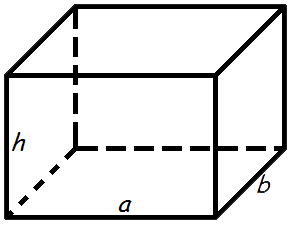
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:
V=a*b*h,
V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.
Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.
Пример первый
Определим объем бака для спирта, при следующих размерах:
Для начала обязательно согласовываем единицы измерения и перемножаем их:
Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.
Пример второй
Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.
Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.
Итак, начнем с сантиметров. Переводим метры в сантиметры:
V = 2240000 сантиметров в кубе.
V = 2.24 метра в кубе.
Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.
Пример третий
Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:
V = a * b * h;
где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5
Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:
V = 37.5 метра в кубе.
Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.
Объем прямоугольника – формула
Для учеников свойственно путать трехмерные и двумерные объекты. Это связано с тем, что на уроках математики изучаются в основном плоские фигуры, а ученик непроизвольно ищет примеры в реальной жизни, где существуют в основном 3д фигуры. Из-за этого возникает и частый вопрос: как найти объем прямоугольника?
Формула объема прямоугольника
Нужно запомнить раз и навсегда: формулы объема прямоугольника не существует.
Характеристики объема у прямоугольника нет, так же как нет ее и у любой двухмерной фигуры.
Аналогом объема служит площадь. Но словосочетание «объем прямоугольника» или объем треугольника» являются грубой ошибкой, и показывает незнание основных геометрических параметров.
Существует формула площади прямоугольника, она равна произведению длины на ширину и известна всем практически с первого класса.
Существует так же и формула объема прямоугольного параллелепипеда. Это фигура, которая состоит из шести граней, каждая из которых является прямоугольником. Очень часто именно эту фигуру по инерции называют прямоугольником, но это ошибка, от которой нужно избавляться.
Объем прямоугольного параллелепипеда равен произведению трех измерений: длины и ширины основания на высоту.
Объем и площадь
Объем и площадь – понятия во многом сходные, но есть и разница, которую стоит понимать. Площадь – это занимаемая часть плоскости. Если любую фигуру вырезать из бумаги, а затем приложить к плоскости, например к другому, более большому, листу, то фигура займет какую-то площадь.
Если фигуру обвести, а затем получившийся контур разбить на квадратики, то получится подсчитать площадь фигуры.
Объем показывает пространство, которое занимает объемная фигура.
Лучше всего объем прямоугольного параллелепипеда представляется так: если в пространстве поместить прямоугольник, провести перпендикулярно плоскости отрезок и плавно поднимать прямоугольник вверх, то результатом движения и станет объем этой фигуры.
Рис. 1. Прямоугольный параллелепипед.
Практически любую объемную фигуру можно представить в виде результата движения плоской фигуры. Например: конус это результат движения прямоугольного треугольника вокруг одного из катетов, а цилиндр результат вращения прямоугольника вокруг своей оси. Прямоугольный параллелепипед это результат вертикального движения прямоугольника-основания вверх
Рис. 2. Результаты вращения плоских фигур.
Двух и трехмерные фигуры
Как отличить двухмерную фигуру от трехмерной? Двухмерная фигура существует исключительно на плоскости. Трехмерная фигура всегда имеет в своем составе элементы плоских фигур: окружности, линии, прямоугольники и т.д.
Рис. 3. Двухмерные и трехмерные фигуры.
Если в составе фигуры можно разглядеть несколько плоских фигур, то фигура трехмерная, если же нет, и фигура состоит только из прямых, отрезков, точек и плоских углов, а саму фигуру можно изобразить на листе бумаги, то перед вами плоская фигура.
Что мы узнали?
Мы узнали, в чем разница двухмерных и трехмерных фигур. Решили, что объема прямоугольника не существует. Существует только площадь прямоугольника или объем прямоугольного параллелепипеда.
Объем прямоугольника – формула расчета
В этой статье мы поговорим о разности определений объема и площади, а так же о прямоугольнике и параллелепипеде. Разделим все понятия, обсудим, как найти площадь и как определить объем.
Определения
Часто в жизни люди совершают математические ошибки. Причем зачастую не в силу какого-то грубого незнания, а просто из-за громоздкости названий. Это не совсем верно, поскольку ведет к увеличению числа ошибок.
Рис. 1. Прямоугольный параллелепипед.
Формулы объема прямоугольника не существует.
Фигура может быть:
Рис. 2. Прямоугольник.
Разделение определений поможет избежать ошибок.
Двумерная фигура характеризуется периметром и площадью. Трехмерная имеет периметр, площадь поверхности и объем. Как понять, есть ли объем у фигуры? Достаточно представить себе, что засыпаешь в нее песок. Задержится ли он в фигуре?
В трехмерной: конусе, цилиндре, параллелепипеде – песок останется лежать, заполняя собой внутренне пространство (то есть объем). В двумерной песок просто насыплется сверху. Разделочную доску нельзя заполнить песком, так же как и нельзя найти объем прямоугольника.
Объем и площадь
Объем это пространственная характеристика. Она показывает, сколько место фигура занимает в пространстве или сколько нужно сыпучего материала или воды, чтобы заполнить фигуру изнутри.
Площадь это двумерная характеристика. Она показывает, к примеру, сколько места займет фигура на столе. Если нам нужно понять, сколько места занимает лист на столе, то считаем площадь, для того, что понять вместится ли учебник в ящик стола, нужно посчитать объем.
Из двумерных прямоугольников составляют трехмерную фигуру, которую называют прямоугольным параллелепипедом. Прямоугольный параллелепипед состоит из шести прямоугольников, которые называют гранями. Четыре боковых грани равны между собой, так же как равны между собой две оставшиеся грани-основания.
Чтобы найти площадь прямоугольника нужно перемножить между собой две стороны, выходящие из одной точки, то есть смежные. Для того, чтобы найти площадь поверхности прямоугольного параллелепипеда нужно сложить площади всех его граней.
Удивительно, но понятие объема появилось еще в Древней Греции. Им оперировал Евклид, Аристотель и Архимед. Но определение было размытым и неточным. Древние ученые увлекались двумерным пространством. Точное определение объема было дано лишь в 19 веке учеными Пеано и Жорданом.
Чтобы найти объем прямоугольного параллелепипеда, нужно так же перемножить между собой стороны, выходящие из одной точки. Но в пространстве их будет три: длина, ширина и высота.
Рис. 3. Трехмерная фигура.
Что мы узнали?
Мы разделили понятия фигур по пространственным характеристикам. Узнали как создается прямоугольный параллелепипед и разделили параллелепипед и прямоугольник, поговорили о расчете площади и объема. Привели примеры геометрических фигур из реальной жизни. Узнали, что объема прямоугольника не существует.