как узнать объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда
С научной точки зрения прямоугольный параллелепипед это объемная фигура, состоящая из 6 граней — прямоугольников. А если по-простому, то кирпич, прямоугольный бассейн или садовый бак, кирпич, спичечный коробок — все это прямоугольные параллелепипеды.
Как видим, эта фигура встречается в жизни довольно часто. И не менее часто возникает потребность найти объем такой фигуры. К примеру, чтобы знать какого размера делать бассейн, чтоб он вместил определенное количество воды или каким делать бак на дачном участке. Именно для этого мы сделали наш калькулятор, который позволит найти объем прямоугольного параллелепипеда мгновенно, в режиме онлайн. Все, что от вас требуется — знать длину, ширину и высоту объекта, ввести их в поля калькулятора и получить результат.
Как найти объем прямоугольного параллелепипеда.
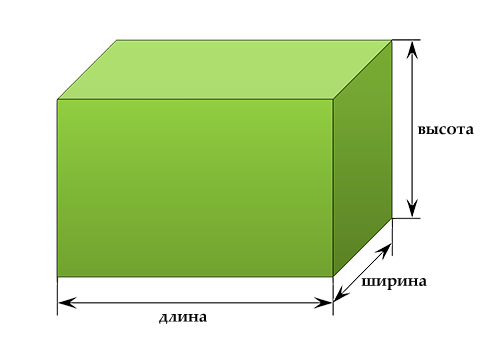
Вообще, очень просто. Если мы знаем длину, ширину и высоту, то достаточно их перемножить. Полученное число и есть искомый объем. Важно — объем измеряется в кубических метрах, сантиметрах, дециметрах и т. д. В итоге, если обозначить длину как a, ширину как b, высоту как c, а объем общепринятым способом — V, то формула для расчета объема прямоугольного параллелепипеда будет выглядеть таким образом:
Как видим, она очень проста для запоминания.
Рассмотрим на примере.
Какой объем воды содержит бассейн, если его длина 10 метров, ширина 3 метра, а глубина 1,5 метра?
Умножив, получим 10 x 3 x 1,5 = 45 м 3 или, другими словами, 45 кубических метров.
Предлагаем также рассчитать объем куба и шара.
Как найти объем прямоугольного параллелепипеда?
Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.
Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.
Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.
Основные особенности и формула для расчета
Для того чтобы найти объем параллелепипеда необходимо:
Это все предельно просто и не таит никаких подводных камней. Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
При этом важно знать, что определить параметр можно в сантиметрах, кубометрах, дециметрах и некоторых других размерностях в зависимости от требований. Если говорить о Международной системе единиц (СИ), параметр рассчитывают в сантиметрах. Это оптимальный вариант. Но при желании всегда можно перевести значение в требуемые размерности.
Формула расчета в двух вариантах
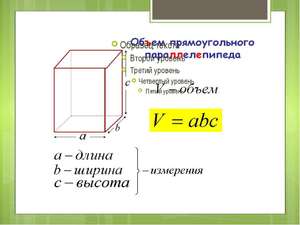
Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.
Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
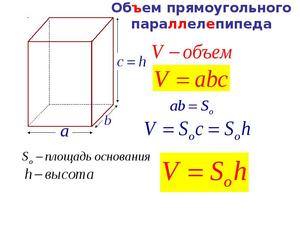
Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.
При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.
О чем еще следует знать для правильности расчета?
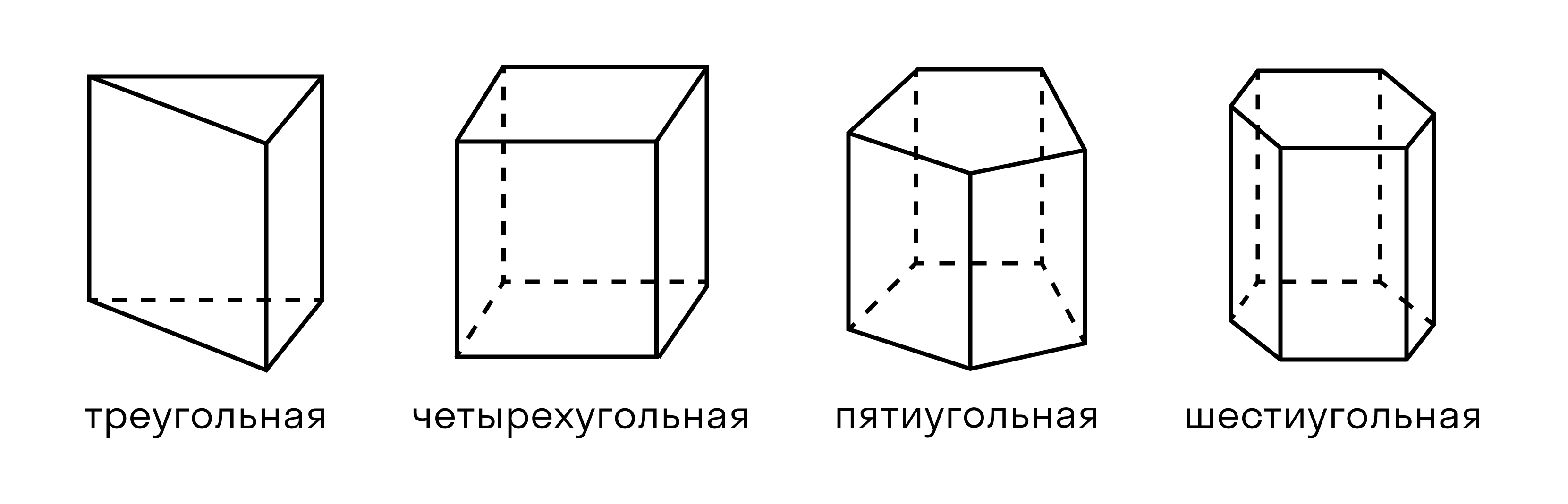
Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся. Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.
Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.
Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.
Видео
Видео поможет вам научиться находить объем прямоугольного параллелепипеда.
Объем параллелепипеда
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.
Два свойства объёма
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Давайте вспомним, какие виды параллелепипедов бывают.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.
Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.
Какие бывают призмы:
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
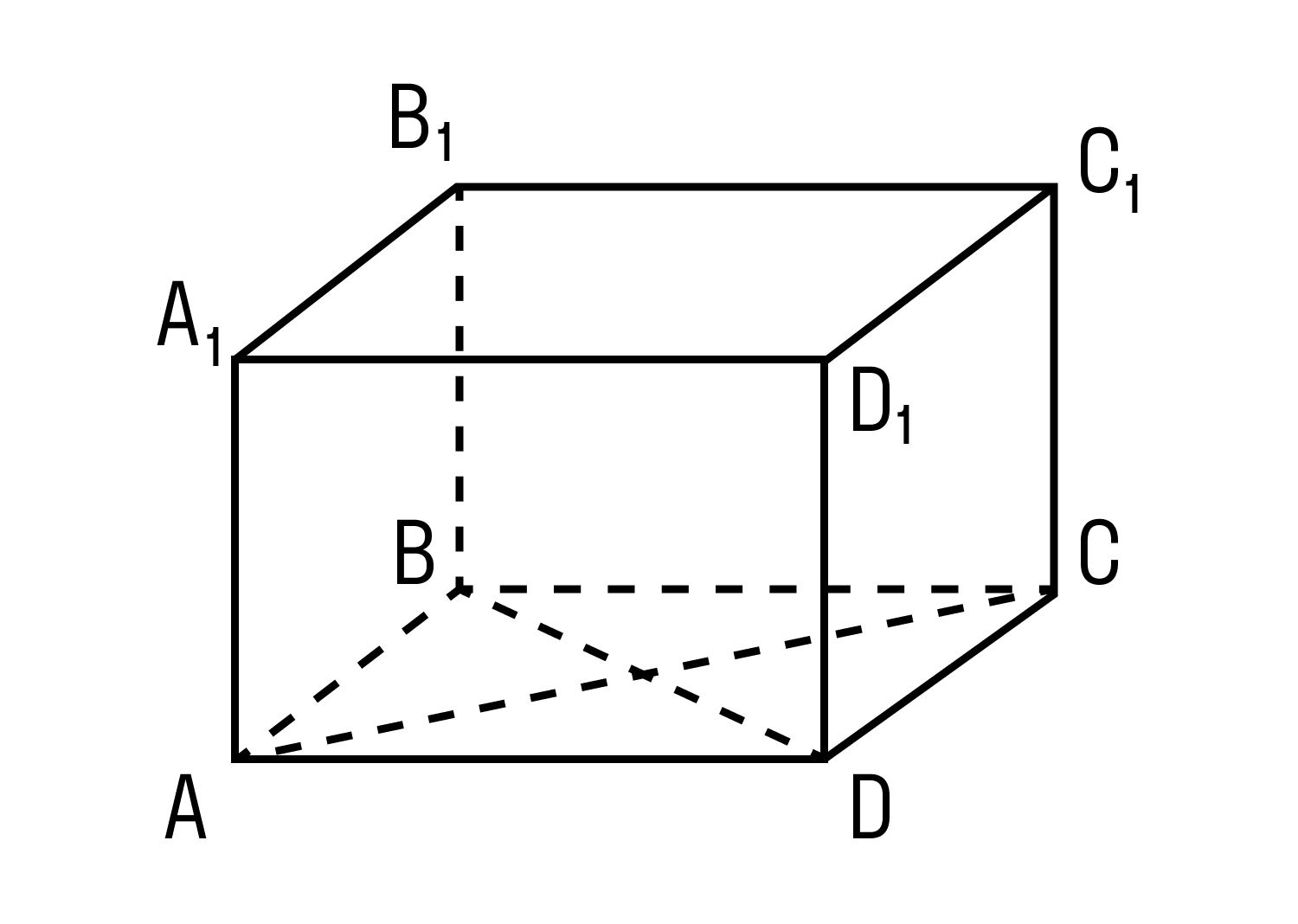
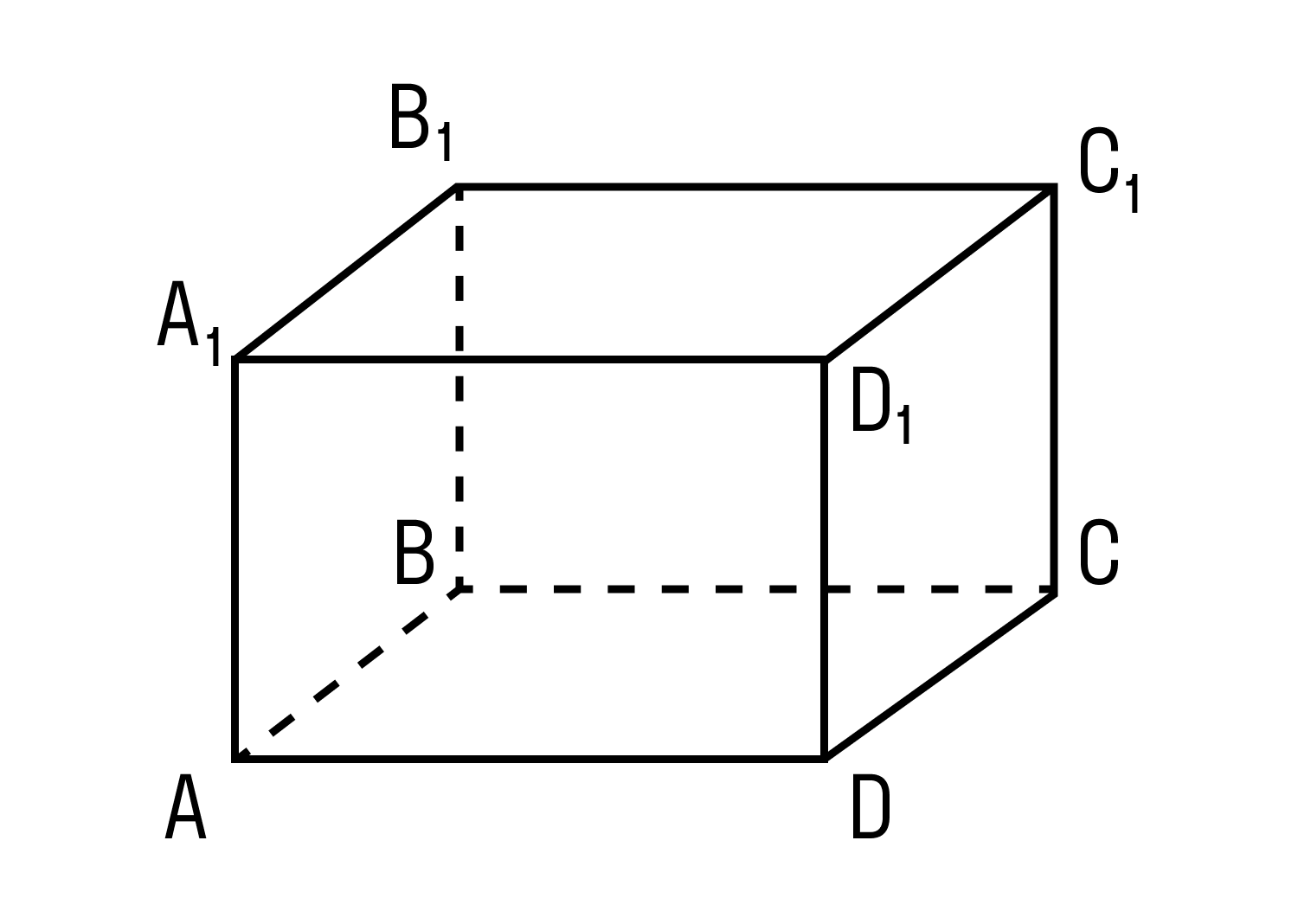
Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
| a | = |
| b | = |
| h | = |
Ввод данных в калькулятор для вычисления объема прямоугольного параллелепипеда
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины, конвертером единиц площади и конвертером единиц объема.
Дополнительные возможности калькулятора для вычисления объема прямоугольного параллелепипеда
Теория. Объем прямоугольного параллелепипеда.
Формула для вычисления объема прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Объемы фигур. Объем параллелепипеда.
Объем прямоугольного параллелепипеда, формула.
Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда
6 граней, а они, в свою очередь, являются параллелограммами.
Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.
Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и
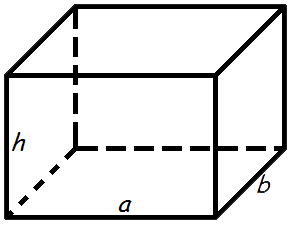
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
a – длина параллелепипеда,
b – ширина параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница
Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями
прямоугольного параллелепипеда.
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это
Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.
Объем прямого параллелепипеда, формула.
Как найти объем параллелепипеда?
Площадь боковой поверхности параллелепипеда, формула:
где Ро — периметр основания,
Площадь полной поверхности, формула
где Sо — площадь основания
Формула объёма прямого параллелепипеда:
Объем произвольного параллелепипеда.
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.
Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного
произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят
Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель
Грама указанных 3х векторов равен квадрату их смешанного произведения.

 Введите данные:
Введите данные: