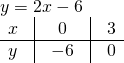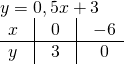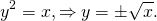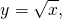как узнать обратима ли функция
Обратимые и обратные функции
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Примеры обратимых функций:
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
Примеры обратных функций:
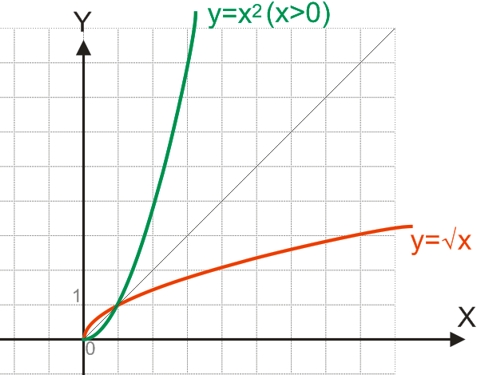
Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:
Графики функций будут симметричны относительно прямой y=x:
Функция y=arcsin(x)
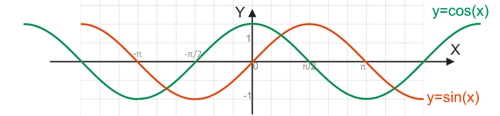
Поскольку функция y=sin(x) является периодической, она не является обратимой.
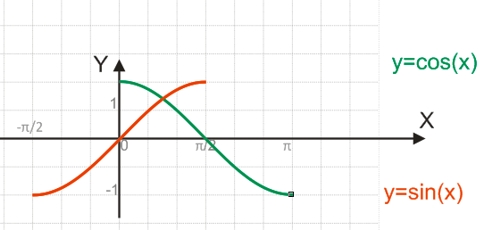
Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.
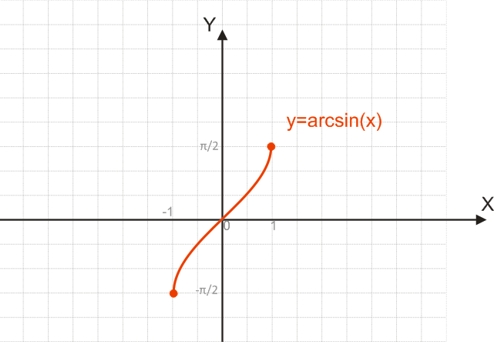
График функции y=arcsin(x):
Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.
Функция y=arccos(x)
Поскольку функция y=cos(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.
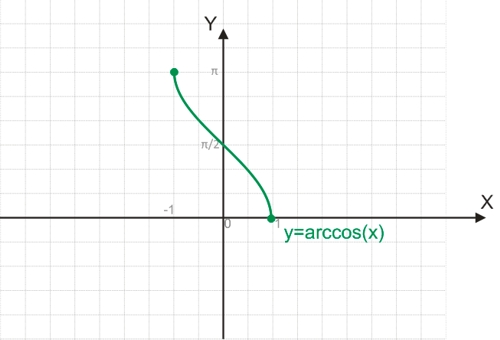
График функции y=arccos(x):
Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.
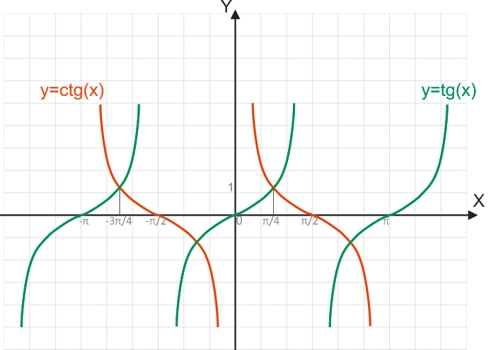
Функция y=arctg(x)
Поскольку функция y=tg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.
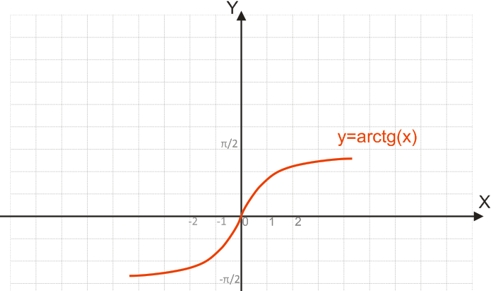
График функции y=arctg(x):
Функция y=arcctg(x)
Поскольку функция y=ctg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.
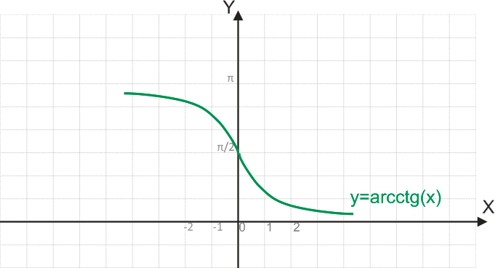
График функции y=arcctg(x):
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Алгебра
План урока:
Взаимно обратные функции
Напомним, что любая функция у = у(х) представляет собой некоторое правило, которое устанавливает соответствие между значениями х и значениями у. В частности, функция у = х 2 ставит в соответствие каждому действительному числу его квадрат. Приведем таблицу, содержащую значения этой функции для целых аргументов от – 2 до 2:
Но если есть соответствие между х и у, то должно существовать и обратное соответствие между у и х. Действительно, строки таблички можно «перевернуть» и она примет следующий вид:
Мы получили два взаимно обратных соответствия. Однако второе из них функцией не является, ведь функция должна ставить в соответствие своему аргументу только одно значение функции. Однако, судя по второй таблице, числу у = 1 соответствует сразу два х: х = – 1 и х = 1. В таком случае математики говорят, что исходная функция у = х 2 является необратимой.
Теперь «перевернем таблицу» и получим следующее:
Мы видим, что как каждому значению х соответствует единственное значение у, так и наоборот, каждому у соответствует единственное значение х. В математике для подобных соответствий используют понятие взаимно-однозначное соответствие.
Для лучшего понимания этого определения отвлечемся от чисел. Пусть в футбольном чемпионате играет несколько команд. Они образуют множество Х команд-участниц соревнования. За множество У примем отдельных футболистов, выступающих на турнире. Каждому игроку соответствует единственная команда, за которую он выступает, но обратное неверно – каждой команде соответствует несколько игроков. Значит, это пример соответствия, не являющегося взаимно-однозначным.
Пусть тренеры команд образуют множество Z. Каждый тренер тренирует лишь одну команду, и наоборот, каждую команду тренирует единственный тренер. Значит, между множествами X и Z есть взаимно-однозначное соответствие.
Вернемся к функциям. Если соответствие, которое задает функция у = у(х), является взаимно-однозначным, то каждому значению у будет соответствовать единственное значение х. Значит, существует некоторая функция х = х(у). Пары функций у = у(х) и х = х(у) называются взаимно обратными функциями.
Ещё раз скажем, что не для любой функции существует обратная функция, ведь не все они определяют взаимно-однозначное соответствие. Если всё же для у = у(х) есть обратная функция х = х(у), то у = у(х) называют обратимой функцией.
Покажем, какие функции являются обратными, на примере пары у = 4х + 12 и у = 0,25х – 3. Возьмем, например, значение х = 5 и подставим его в у = 4х + 12:
у = 4х + 12 = 4•5 + 12 = 32
Получили 32. Подставим это число в обратную функцию:
у = 0,25х – 3 = 0,25•32 – 3 = 8 – 3 = 5
Получили именно то число, которое первоначально подставили в первую функцию! Возьмем другое произвольное число, например, 10, и подставим его в у = 4х + 12:
у = 4•10 + 12 = 40 + 12 = 52
Полученный результат подставляем в у = 0,25х – 3:
у = 0,25•52 – 3 = 13 – 3 = 10
Снова получили исходное число! Выберете сами ещё несколько произвольных чисел и убедитесь, что и с ними будет происходить то же самое.
Посмотрим, как получить обратную функцию. Пусть дана зависимость
Это, по сути, выражение для вычисления у. Выразим из него х:
Получили зависимость х от у. Чтобы мы получили из нее обратную функцию, необходимо просто поменять местами буквы х и у:
Убедитесь самостоятельно на нескольких примерах, что полученная функция обратна функции у = 5х + 20.
Пример. Найдите функцию, обратную зависимости у = 1/(х + 7).
Решение. Умножим обе части равенства у = 1/(х + 7) на (х + 7):
Далее поделим обе части нау:
Перенесем семерку вправо и получим формулу для вычисления х:
Для получения обратной функции просто меняем х и у местами:
Предположим, у нас есть у= у(х), чей график нам известен, и необходимо построить график взаимно обратной функции. Как это сделать? Если одна точка на координатной прямой имеет координаты (a; b) и принадлежит функции у = у(х), то, обратной функции должна принадлежать точка (b; a):
Эти точки симметричны относительно прямой у = х:
Поэтому для построения графика обратной функции достаточно симметрично отобразить его относительно прямой у = х.
С помощью этого правила построим график функции, обратной у = х 3 :
Практика показывает, что не все школьники (да и взрослые тоже) понимают, что означает симметричность относительно прямой у = х, ведь эта прямая наклонена. Здесь требуется довольно высокий уровень пространственного мышления. Куда проще понять симметрию относительно вертикальной или горизонтальной линии. Поэтому мы покажем ещё один способ построения обратных функций, который состоит из двух этапов.
Он заключается в том, что сначала график отображают симметрично относительно вертикальной оси Оу:
На втором этапе полученное отображение поворачивают по часовой стрелке относительно начала координат:
Заметим важное правило. При построении обратной функции области определения и области значений меняются местами. Действительно, если какое-то число входит в область значения функции, то это значит, что его можно подставить в обратную функцию. Но это в свою очередь означает, что она входит в область определения обратной функции. Проиллюстрируем это правило картинкой:
До сих пор мы рассматривали способы построения обратных функций, но ведь в самом начале урока говорилось о том, что обратная функция существует не всегда. Действительно, попытаемся построить обратную функцию для у = х 2 :
Получилась та же парабола, но «лежащая на боку». Является ли она графиком функции? Нет. На рисунке проведена вертикальная линия, которая пересевает график в двух точках. Это значит, что одному значению х (в данном случае х = 5) соответствует сразу два значения у. Но подобное соответствие не является функцией. Это значит, что у = х 2 – необратимая функция.
Есть ли какой-то признак, позволяющий быстро сказать, является ли функция обратимой? Оказывается, есть. Если функция строго монотонна (то есть либо только возрастает, либо только убывает), то это гарантирует, что она ещё и обратима. Покажем это с помощью рисунков. Известно, что каждому значению строго монотонной функции соответствует лишь один аргумент. С точки зрения геометрии это означает, что любая горизонтальная линия пересекает монотонную функцию не более чем в одной точке:
К слову, это свойство мы использовали для решения некоторых уравнений. Теперь отобразим график симметрично прямой у = х, причем также отобразим и горизонтальные линии:
Горизонтальные линии превратились в вертикальные, при этом они всё также пересекают график не более чем в одной точке. Но это как раз и означает, что график задает функцию, а не какое-то другое соответствие. Отсюда делаем вывод – любая строго монотонная функция обратима.
Можно сделать вывод – обратимость функции зависит не только от самого вида функции, но и от того, на какой области определения ее рассматривают.
Кубический корень
Ранее мы изучили понятие квадратного корня. Напомним, что извлечение квадратного корня – это операция, обратная возведению в квадрат. Другими словами, функция
Можно дать и другое определение, не использующее понятие функции:
Например, мы знаем, что число 5 в кубе равно 125:
Это значит, что кубический корень из 125 равен 5.
Для обозначения кубического корня используют тот же знак радикала, что и для квадратного корня. Чтобы их отличать друг от друга, в случае с кубическим корнем перед знаком радикала ставят тройку:
Заметим важное отличие кубического и квадратного корня. Мы привыкли, что под знаком радикала не должно стоять отрицательное число. Но кубический корень из отрицательного числа извлечь можно. Например, мы знаем, что (– 6) 3 = – 216. Отсюда следует, что
График кубического корня можно получить, просто построив функцию, обратную у = х 3 :
Корни n-ой степени
Аналогично кубическому корню можно ввести понятие и корня произвольной n-ой степени.
Для обозначения корня n-ой степени используется знак радикала, перед которым стоит число n. Приведем пример. Мы знаем, что 2 5 = 32. Это значит, что корень 5-ой степени из 32 равен 2:
Если же показателем n является нечетное число, то график у = х n будет схож с графиком у = х 3 :
Если n нечетно, то корень можно извлечь и из отрицательного числа. Так, известно, что (– 3) 7 = – 2187. Это значит, что корень седьмой степени из (– 2187) равен (– 3):
Очевидно, что корень получится отрицательным, если под ним стоит отрицательное число. Если же подкоренное выражение положительно, то и сам корень положителен. Более того, можно заметить, что корень из отрицательного числа равен корню из противоположенного ему положительного числа, взятого со знаком минус:
В общем случае графики всех корней нечетных степеней будут похожи на график кубического корня:
При четном значении n корень n-ой степени нельзя извлечь из отрицательного числа. Действительно, попробуем возвести в четную степень положительное число:
Получили другое положительное число. Теперь попробуем возвести в четную степень отрицательное число:
(– 5) 4 = (– 5)•(– 5)•(– 5)•(– 5) = 625
Результат снова положительный! Минусы у отрицательных чисел «сократились» друг с другом, и получилось положительное произведение. Но раз при возведении в четную степень всегда получается неотрицательное число, значит, и под четным корнем должно также стоять неотрицательное число. Поэтому подкоренное выражение не может быть отрицательным.
Арифметические корни n-ой степени
Мы видим, что складывается не очень удобная для математиков ситуация: корни n-ой степени из отрицательного числа можно извлечь, если n – нечетное число, но при четном n такая операция уже недопустима. Это порождает много проблем при работе с корнями. Для устранения этих проблем вводится понятие арифметического корня степени n. Его особенность в том, что он всегда извлекается из неотрицательного числа и сам принимает значения, не меньшие нуля.
Заметим, что корень нечетной степени из отрицательного числа всегда можно выразить с помощью арифметического корня, просто вынеся знак минус из-под корня:
Поэтому арифметических корней вполне хватает для работы в любых ситуациях.
Определение корня можно записать в более формализованном виде:
Проиллюстрируем использование этой формулы:
Свойства корня n-ой степени
Далее рассмотрим некоторые свойства корней степени n, помогающие вычислять их значения. Сразу скажем, что они во многом идентичны свойствам квадратного корня.
Для доказательства этого свойства правую часть в n-ую степень:
Приведем примеры использования этого свойства:
Отсюда следует, что множители можно вносить и выносить из-под знака корня:
Следующее свойство помогает извлекать корни из дробей.
Доказывается это свойство так же, как и первое. Возведем в n-ую степень правую часть формулы:
Продемонстрируем применение доказанного тождества:
Заметим, что если под корнем находится степень какого-то числа, то ее вынести из-под радикала:
Доказать это можно, разложив число a m в произведение:
Всего справа стоит m множителей. Теперь извлечем корень степени n:
Справа всё те же m множителей, а потому
Таким образом, получаем, что
Покажем несколько примеров использования этого правила:
Далее посмотрим, как извлекать корень из другого корня.
Для доказательства возведем корень в левой части формулы в степень mn:
По определению корня получаем, что
Проиллюстрируем использование данного правила:
Последнее свойство, которое нам осталось изучить, называют основным свойством корня.
Доказательство записывается всего в одну строчку:
Степени в корне и под ним можно «сокращать»:
Сравнение корней
Естественно, что большинство корней – это не целые, а иррациональные числа, которые довольно сложно вычислять. Тем не менее есть несколько правил, которые помогают оценивать их значение. Из графиков корней видно, что все они являются возрастающими функциями. Поэтому, если необходимо сравнить два корня одной степени, достаточно сравнить их подкоренные выражения. Тот корень, у которого под корнем стоит большее число, и будет больше
В частности, справедливы неравенства:
В случае, если у корней различаются степени, следует постараться преобразовать их так, чтобы степени всё же совпали.
Пример. Сравните числа
Решение. Преобразуем первое число, чтобы у нас получился корень шестой степени:
Так как 121 > 119, то и
Пример. Сравните числа
Решение. Сначала избавимся от вложенных корней:
Получили два кубических корня. Меньше тот из них, у которого под радикалом меньшее число:
Пример. Сравните корни
Решение. Имеем корни 7-ой и 4-ой степени. К какой одинаковой степени можно привести оба корня? Это число 28, ведь оно представляет собой произведение 7•4:
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?
Обратная функция
Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x.
Еще один пример взаимно-обратных функций:
Вспомним определение функции. Числовая функция y = f(x) — это такое соответствие между двумя числовыми множествами A и B, при котором каждому числу x ∈ A отвечает одно-единственное число y ∈ B. Множество A называется при этом областью определения функции, множество B — областью значений.
Пусть соответствие f является взаимно-однозначным:

Тогда существует функция g, которая действует в обратную сторону: каждому числу y ∈ B она ставит в соответствие одно-единственное число x ∈ A, такое, что f(x) = y:

Функция g называется обратной к функции f. Точно так же и функция f будет обратной к функции g.
Если мы возьмём какое-либо число x ∈ A и подействуем на него функцией f, то получим число y = f(x) ∈ B. Теперь на полученное число y подействуем функцией g. Куда попадём? Правильно, вернёмся к исходному числу x. Это можно записать так:
 | (1) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число 3 в степень x, а затем совершить обратное действие — взять от полученного числа 3 x логарифм по основанию 3 — мы вернёмся к исходному числу x:
Графики взаимно-обратных функций симметричны относительно прямой у = x.
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
1) Выражаем из формулы функции x через у. Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Обратная функция. Урок алгебры в 10-м классе (профильный уровень)
Разделы: Математика
Воспитательная: формировать коммуникативную компетентность.
Оборудование: компьютер, проектор, экран, интерактивная доска SMART Board, раздаточный материал (самостоятельная работа) для работы в группе.
Ход урока.
1. Организационный момент.
Цель – подготовка учащихся к работе на уроке:
— настрой учащихся на работу, организация внимания;
— сообщение темы и цели урока.
2. Актуализация опорных знаний учащихся. Фронтальный опрос.
Для учащихся на интерактивной доске демонстрируется график функции. Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.
По окончании исследования учитель сообщает, что сегодня на уроке они познакомятся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы записаны на обыкновенной доске и в виде раздаточного материала есть у каждого ученика (раздается до урока)
3. Объяснение нового материала.
Цель — формировать знания по новой теме в соответствии с программным материалом; изучить свойство обратимости функции и научить находить функцию, обратную данной; развивать предметную речь.
Учитель проводит изложение материала в соответствии с материалом параграфа. На интерактивной доске учитель проводит сравнение графиков двух функций, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет, тем самым подводит учащихся под понятия обратимой функции.
Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Определение 1: Функцию y=f(x), x X называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Учащимся предлагается сделать вывод о связи между областью определения и множеством значений обратных функций.
Для рассмотрения вопроса о способах нахождения функции обратной данной, учитель привлек двух учащихся. Ребята накануне получили задание у учителя самостоятельно разобрать аналитический и графический способы нахождения функции обратной данной. Учитель выступил в роли консультанта при подготовке учащихся к уроку.
Сообщение первого ученика.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учащийся привел примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима
Затем ученик знакомит учащихся со способом нахождения обратной функции, заданной аналитически.
Затем решает два примера на нахождение функции обратной данной.
Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим 
Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.
Ответ:
Во время объяснения на интерактивной доске выполняется следующее задание:
Построить в одной системе координат график функции 
4. Первичное закрепление нового материала.
Цель – установить правильность и осознанность понимания изученного материала, выявить пробелы первичного осмысления материала, провести их коррекцию.
Учащиеся делятся на пары. Им раздаются листы с заданиями, в которых они и выполняют работу в парах. Время на выполнение работы ограничено (5-7 мин). Одна пара учащихся работает на компьютере, проектор на это время выключается и остальным ребятам не видно, как работают учащиеся на компьютере.
По окончании времени (предполагается, что с работой справилось большинство учащихся) на интерактивной доске (вновь включается проектор) показывается работа учащихся, где и выясняется в ходе проверки правильность выполнения задания в паре. При необходимости учителем проводится коррекционная, разъясняющая работа.
Самостоятельная работа в парах
5. Итог урока. По вопросам, которые были заданы перед началом лекции. Объявление оценок за урок.
Домашнее задание §10. №№ 10.6(а,в) 10.8-10.9(б) 10.12 (б)
Алгебра и начала анализа. 10 класс В 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2007 год