как узнать пересекает ли прямая плоскость

Точка пересечения прямой и плоскости онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Точка пересечения прямой и плоскости − теория, примеры и решения

1. Точка пересечения плоскости и прямой, заданной в каноническом виде

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L₁:

,

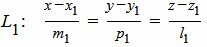(1)

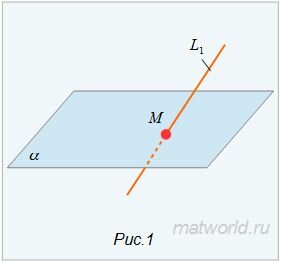
Найти точку пересечения прямой L₁ и плоскости α (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:

Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L₁ и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L₁ лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L₁ и плоскости α.

Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же

2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L₁ в параметрическом виде:

Задачу нахождения нахождения точки пересечения прямых L₁ и плоскости α можно решить разными методами.

Метод 1. Приведем уравнения прямой L₁ к каноническому виду.

Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:

Так как левые части уравнений (10) равны, то можем записать:

Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямой L₁ и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):

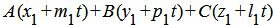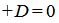(13)

Откроем скобки и найдем t:

Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L₁ лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.

Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L₁ и плоскости α подставим полученное значение t из (14) в (8).

3. Примеры нахождения точки пересечения прямой и плоскости.

Пример 1. Найти точку пересечения прямой L₁:

Представим уравнение (15) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (17) и (18):

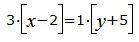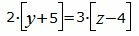Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

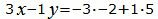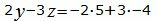Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):

Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

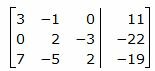Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:

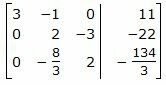Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:

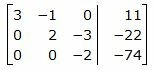Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:

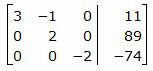Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:

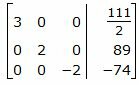Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

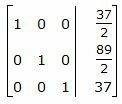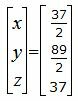Ответ. Точка пересечения прямой L₁ и плоскости α имеет следующие координаты:

Пример 2. Найти точку пересечения прямой L₁:

Представим уравнение (22) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (24) и (25):

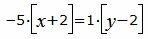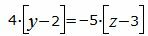Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

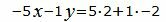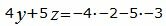Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):

Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:

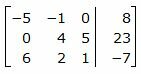Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:

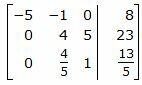Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:

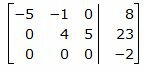Из расширенной матрицы восстановим систему линейных уравнений:

Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L₁ и плоскость α не пересекаются, т.е. они параллельны.

Ответ. Прямая L₁ и плоскость α параллельны, т.е. не имеют общую точку.

Пример 3. Найти точку пересечения прямой в параметрическом виде L₁:

Решение. Для нахождения точки пересечения прямой L₁ и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):

Упростив уравнение, получим:

Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L₁ удовлетворяет уравнению плоскости α. Следовательно прямая L₁ лежит на плоскости α.

Ответ. Прямая L₁ лежит на плоскости α.

Источник

Пересечение прямой с плоскостью

Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми

Плоскость и пересекающая ее прямая занимают общее положение.

На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :

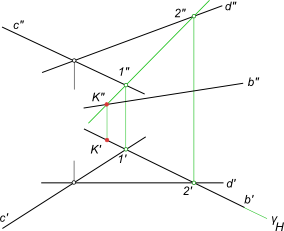
2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γ_H пересекает прямые c` и d`;

3) определяем точку K»=l»∩b». Зная K», находим K` на пересечении b` с линией проекционной связи.

Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми

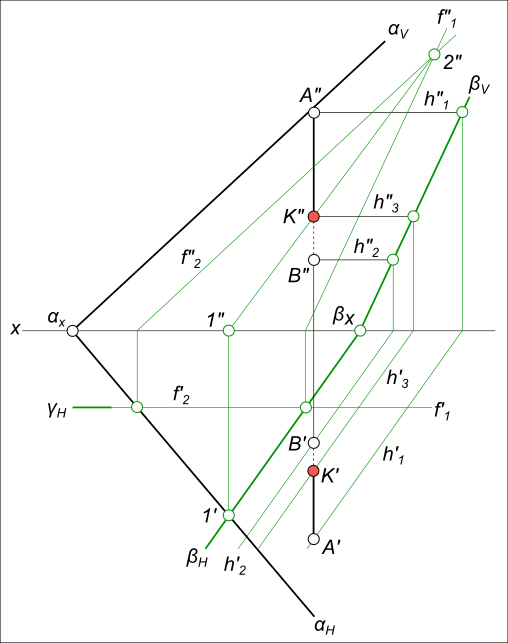
Задача по нахождению точки встречи прямой с плоскостью заданной следами.

Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).

При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.

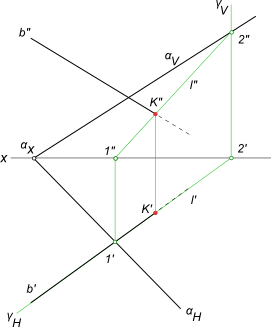
Найти точку встречи профильной прямой AB с плоскостью α заданной следами

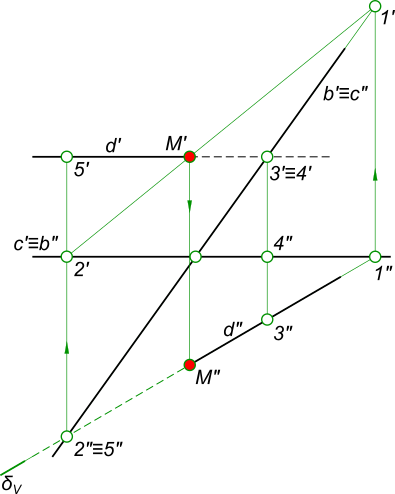
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость

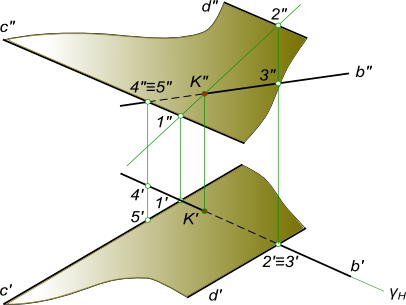
Алгоритм выполнения геометрических построений: 1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α; 3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K» точки K находим в пересечении d» с линией проекционной связи.

Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник