как узнать периметр круга по диаметру
Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
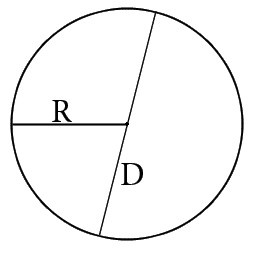
где R –это радиус, а D – это диаметр
Периметр круга — онлайн калькулятор
Круг – двухмерная геометрическая фигура, границей которого по определению является окружность. Центром фигуры становится зафиксированная на плоскости точка, равноудаленная от любого места на замкнутой кривой. Прямая линия, соединяющая центр с каждой точкой окружности называется радиусом — R. Рассчитать длину окружности можно по одной из известных величин – радиусу или диаметру.
Достоверная формула для определения периметра и длины круга была выведена древнегреческим математиком Архимедом Сиракузским в III веке до нашей эры. Ученый первый обнаружил закономерность в соотношении общей длины тела к его диаметру, и предложил обозначить константой ∏. Абстрактное число было равно 3,14159265359 … и до бесконечности. Голландский математик Лудольф ван Цейлен рассчитал и ограничил ∏ до 32 знаков после запятой. Константа стала основой для современной формулы вычисления периметра и длины окружности через радиус.
В калькуляторе периметра круга используется классический принцип расчета:
Для вычисления параметров круга, достаточно вставить в строку известное значение радиуса и получить результат.
Примеры вычисления
С помощью удобного инструмента можно быстро и просто найти длину любого круглого тела. Например, чтобы узнать периметр экватора Земли, необходимо подставить значения в поля калькулятора. Согласно географическим данным, экваториальный радиус составляет 6 378.1 километра:
Значение полностью соответствует официально установленной протяженности экватора.
Расчет может применяться не только для определения абстрактных величин. В повседневной жизни формула является одной из самых востребованных. Например, чтобы сделать удачную покупку ювелирного кольца в интернет-магазине, не обязательно примерять десятки изделий для уточнения размера в традиционном бутике. Достаточно сантиметром измерить диаметр старого украшения, и разделить значение на 2. Например, если радиус кольца 9 мм, то длина равна:
Круг – одно из самых распространенных геометрических тел в повседневной жизни. Целая фигура и её отдельные части используются во всех сферах промышленности и народного хозяйства, от крупномасштабного строительства до производства посуды. Необходимость быстро вычислить параметры окружности возникает часто. Онлайн калькулятор периметра круга можно использовать для решения элементарных математических и бытовых задач.
Онлайн калькулятор. Длина окружности. Периметр круга.
Используя этот онлайн калькулятор, вы сможете найти длину окружности.
Воспользовавшись онлайн калькулятором для вычисления длины окружности (периметра круга), вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти длину окружности

Ввод данных в калькулятор для вычисления периметрa окружности
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины.
Теория. Длина окружности
Формулы для вычисления длины окружности.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Способы расчета периметра круга и длины окружности
Периметр круга — что это, определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159. \)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, равное 3,14
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.