как узнать период функции
Узнать ещё
Знание — сила. Познавательная информация
Как найти период функции
Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции
где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.
Найти период функции:
Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции
А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то
А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции
А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть
Как определить периодичность функции
Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
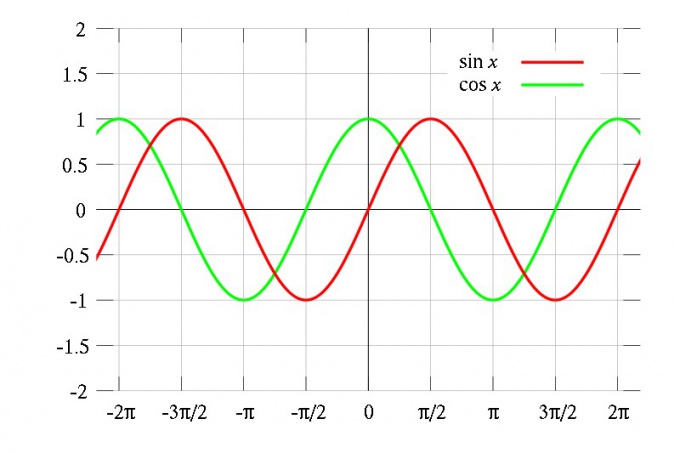
Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Периодические функции
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.
Дадим определение периодической функции:
Например, — периодические функции.
Для функций и период
Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:
1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения
График функции может выглядеть, например, вот так:
Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.
2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).
Построим график функции при
Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.
Период функции равен 2. Повторим периодически участок длины 2, который уже построен.
3. Найдите наименьший положительный период функции
Наименьший положительный период функции равен
График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).
Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции
4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции
Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.
Исследование функции на периодичность
Разделы: Математика
Цель: обобщить и систематизировать знания учащихся по теме “Периодичность функций”; формировать навыки применения свойств периодической функции, нахождения наименьшего положительного периода функции, построения графиков периодических функций; содействовать повышению интереса к изучению математики; воспитывать наблюдательность, аккуратность.
Оборудование: компьютер, мультимедийный проектор, карточки с заданиями, слайды, часы, таблицы орнаментов, элементы народного промысла
“Математика – это то, посредством чего люди управляют природой и собой”
А.Н. Колмогоров
I. Организационный этап.
Проверка готовности учащихся к уроку. Сообщение темы и задач урока.
II. Проверка домашнего задания.
Домашнее задание проверяем по образцам, наиболее сложные моменты обсуждаем.
III. Обобщение и систематизация знаний.
1. Устная фронтальная работа.
1) Сформируйте определение периода функции
2) Назовите наименьший положительный период функций y=sin(x), y=cos(x)
3). Назовите наименьший положительный период функций y=tg(x), y=ctg(x)
4) Докажите с помощью круга верность соотношений:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)
tg(x+ π n)=tgx, n € Z
ctg(x+ π n)=ctgx, n € Z
sin(x+2 π n)=sinx, n € Z
cos(x+2 π n)=cosx, n € Z
5) Как построить график периодической функции?
1) Доказать следующие соотношения
a) sin( 740º ) = sin(2 0º )
b) cos( 54º ) = cos(-1026º)
c) sin(-1000º) = sin( 80º )
2. Доказать, что угол в 540º является одним из периодов функции y= cos(2x)
3. Доказать, что угол в 360º является одним из периодов функции y=tg(x)
a) tg 375º
b) ctg 530º
c) sin 1268º
d) cos (-7363º)
5. Где вы встречались со словами ПЕРИОД, ПЕРИОДИЧНОСТЬ?
Ответы учащихся: Период в музыке – построение, в котором изложено более или менее завершенная музыкальная мысль. Геологический период – часть эры и разделяется на эпохи с периодом от 35 до 90 млн. лет.
Период полураспада радиоактивного вещества. Периодическая дробь. Периодическая печать – печатные издания, появляющиеся в строго определенные сроки. Периодическая система Менделеева.
6. На рисунках изображены части графиков периодических функций. Определите период функции. Определить период функции.
7. Где в жизни вы встречались с построением повторяющихся элементов?
Ответ учащихся: Элементы орнаментов, народное творчество.
IV. Коллективное решение задач.
(Решение задач на слайдах.)
Рассмотрим один из способов исследования функции на периодичность.
Задача 1. Найдите наименьший положительный период функции f(x)=1+3
Решение: Предположим, что Т-период данной функции. Тогда f(x+T)=f(x) для всех x € D(f), т.е.
Положим x=-0,25 получим
Мы получили, что все периоды рассматриваемой функции (если они существуют) находятся среди целых чисел. Выберем среди этих чисел наименьшее положительное число. Это 1. Проверим, не будет ли оно и на самом деле периодом 1.
Так как
Задача 2. Показать, что функция f(x)=cos 2 (x) периодическая и найти её основной период.
Задача 3. Найдите основной период функции
Допустим Т-период функции, тогда для любого х справедливо соотношение
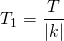
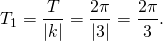
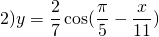
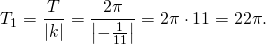
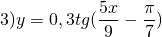
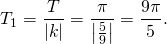
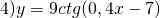










 =1
=1 , n € Z
, n € Z


 , отсюда sinT=0, Т= π n, n € Z. Допустим, что при некотором n число π n действительно является периодом данной функции. Тогда и число 2 π n будет периодом
, отсюда sinT=0, Т= π n, n € Z. Допустим, что при некотором n число π n действительно является периодом данной функции. Тогда и число 2 π n будет периодом
