как узнать площадь 5 угольника

Калькулятор площади пятиугольника

Пятиугольник представляет собой геометрическую фигуру с пятью углами. Существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным и носит название «пентагон».

Геометрия пятиугольника

Пятиугольник — это фигура, которая состоит из пяти соединенных отрезков. Стороны произвольного многоугольника могут соединяться под разными углами, в результате чего фигура может быть невыпуклой. Наиболее ярким примером невыпуклого многоугольника является звезда, а пятиугольника — проекция зубчатой короны, когда два «зубца» выступают над прямоугольным основанием. Выпуклый многоугольник — это фигура, продолжение отрезков которого не пересекает других сторон. Если же мы продлим отрезки зубцов или лучей звезды, они пересекут другие стороны фигуры.

Пятиугольник в реальности

Невыпуклые геометрические фигуры редко встречаются в человеческой повседневности и обычно представляют собой основания для нестандартных призм. Наиболее распространенным пятиугольником в реальности считается пентагон — правильный многоугольник. Пентагон нашел применение в архитектуре и дизайне, и тезкой фигуры является одно из самых известных зданий Америки — штаб министерства обороны США.

Додекаэдр — платоново тело, каждая из 12 сторон которого является правильным пятиугольником. Додекаэдр используется в различных сферах, но наиболее известным представлением многогранника считается игральная кость d12, которая используется как генератор случайных чисел для настольных ролевых игр.

Несмотря на то, что многие организмы обладают пентасимметрией, например, морские звезды или плоды мушмулы, природные пятиугольные объекты практически не встречаются в природе.

Площадь пентагона

Площадь любой геометрической фигуры — это количественная оценка того, какую часть плоскости ограничивают ее стороны. Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле:

S = n/4 × a 2 × ctg(pi/n),

где n – количество сторон фигуры, a – длина стороны.

Таким образом, если подставить n = 5 и выразить получившееся выражение десятичной дробью, мы получим простую формулу для вычисления площади пентагона:

где a — длина одной стороны.

Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как:

Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных:

Рассмотрим на примерах, как вычислить площадь правильного пятиугольника.

Примеры из жизни

Пентагон

Штаб министерства обороны США — это всемирно известное здание, которое имеет форму правильного пятиугольника. Каждая сторона штаба имеет длину 281 м и мы без проблем можем узнать, какую площадь занимает здание. Для более удобного представления выразим длину в километрах, введем эти данные в форму калькулятора a = 0,281 и получим результат:

Площадь Пентагона составит 0,136 квадратных километров.

Школьная задача

К примеру, необходимо вычислить площадь пентагона, зная, что радиус вписанной окружности составляет 15 см. Мы можем выразить сторону многоугольника через простое соотношение радиуса вписанной окружности и длины стороны a = 1,4131 r, после чего посчитать по формуле его площадь. Проще всего ввести значение радиуса в ячейку «Радиус вписанной окружности r» и получить мгновенный результат:

Кроме непосредственно площади фигуры, калькулятор автоматически подсчитал остальные атрибуты пятиугольника.

Заключение

Пентагон нечасто встречается в реальной жизни, однако при решении производственных вопросов или школьных задач вам может понадобиться рассчитать площадь или периметр правильных многоугольников. Наш каталог калькуляторов к вашим услугам.

Источник

Площадь многоугольника

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Пример многоугольника

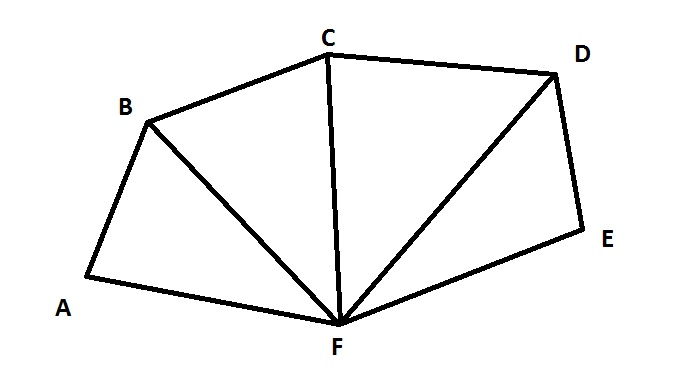
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Источник

Площадь правильного пятиугольника

Площадь правильного пятиугольника — это число, характеризующее правильный пятиугольник в единицах измерения площади.

Правильный пятиугольник (пентагон) — это пятиугольник, у которого все стороны и углы равны.

[править] Обозначения

n — число сторон, n = 5;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α = π/5;

P₅ — периметр правильного пятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;

S₅ — площадь правильного пятиугольника.

[править] Формулы

[math]S_5=\frac<\sqrt<25+10\sqrt<5>>><4>a^2 \Leftrightarrow[/math] [math]\Leftrightarrow S_5=5S_<\triangle>, \ S_<\triangle>=\frac<\sqrt<25+10\sqrt<5>>><20>a^2 \Leftrightarrow[/math] [math]\Leftrightarrow S_5=\frac<1><2>P_5r, \ P_5=5a, \ r=\frac<\sqrt<25+10\sqrt<5>>><10>a \Leftrightarrow[/math] [math]\Leftrightarrow S_5=\frac<5\sqrt<10+2\sqrt<5>>><8>R^2, \ R=\frac<\sqrt<50+10\sqrt<5>>><10>a \Leftrightarrow[/math] [math]\Leftrightarrow S_5=5\sqrt<5-2\sqrt<5>>r^2, \ r=\frac<\sqrt<5>+1><4>R[/math]

[править] Другие многоугольники

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

Навигация

Инструменты

Источник

Как посчитать площадь многоугольника?

Не смог найти ответ на свой вопрос через яндекс и гугл, поэтому решил обратиться к вам за помощью.

Есть формулы для расчета площади правильного n-угольника, но мне нужно для неправильного.

Задача такая: дана фигура с n сторонами (например 7), мы знаем только длины всех сторон и нужно найти площадь фигуры.

Знаю, что в том же Blender и autocad можно соеденить точки (углы) сторон многоугольника, нажать на волшебную кнопку для подсчета площади и вуаля, есть ответ. Какой метод используется в этих случаях? Можно формулу, алгоритм или название метода подсчета.

Задача такая: дана фигура с n сторонами (например 7), мы знаем только длины всех сторон и нужно найти площадь фигуры.

Просто по длинам сторон задача не имеет общего решения даже для 4 сторон, какие там нафиг n

Нужны углы или координаты, далее уже есть формулы типа Гаусса

Всё так. Я уже отписался про формулу площади Гаусса. Основная проблема это переход к системе координат. Можно связать длины сторон с координатами через формулу (Спасибо @Ученик Кодзимы). Но можно ли решить полученную систему (ы) я не знаю. Думаю надо копать в этом направлении

Рздели на треугольники и подсчитай сумму площадей трегольников 🙂

Площадь каждлого треугольника по основанию и высоте считай.
S=1/2 основание умножить на высоту)

Вариант хороший, но откуда высоты взять?

Я так и делал. Но мне нужна либо готовая формула, либо как то автоматизировать способ подсчета через треугольники. Мне вот интересно, как тот же блендер и автокад считают.

Так а в чем проблема вывести формулу оснрвывающуюся на количестве сторон (а значит и известных углах) и длине стороны? Смотришь как ты посчитал и подставляешь вместо циферок буковки

Если известно колличество углов то и углы известны, нет?

Я уже нее соображаю в столь поздний час. А как зная количество сторон и углов, а также длины сторон мы сможем найти все углы?

А как посмотреть как блендер считает?

Вроде открытый был всегда он. В исходниках и посмотреть.

ну и что он там насчитает не зная диагоналей

я не понимат, ведь при одних и тех же сторонах может быть разная площадь, например многоугольник вытянутый или один из углов вогнутый. Так что имхо информации ни разу не достаточно

А может, двойным интегрированием попробовать?

Еееееее. Давайте сделаем из вопросов ответы маил.

Мне через личку уже подсказали про последний способ из данной статьи. Называется формула площади Гаусса. Минус в том что, нужно всё переводить в координаты.

Можно аппроксимировать. Могу предложить заполнить площадь фигуры равными квадратами без пересечения со сторонами и с пересечениями. Истинную площадь (приближённо) найти как среднее из площадей. Для повышения точности уменьшать размер квадратов до тех пор, пока разница вычисленных площадей между итерациями (до и после уменьшения) составит не более требуемой относительной погрешности (например 0,001).
Оптимизировать процесс расчёта можно уменьшая размер только тех квадратов, которые находятся рядом с границей n-мерной фигуры.

И как уже отметили выше, нужны либо углы между сторонами, либо координаты точек.

Пилишь многоугольник на правильные фигуры, считаешь их площадь, складываешь. По-другому площадь любых неправильных фигур не считается. Площадь правильного многоугольника как-то можно посчитать через формулу, но я не помню как. Ы.

Источник

Калькулятор площади многоугольника

Многоугольник или полигон — геометрическая фигура, которая имеет n-ное количество углов. В общем случае многоугольник — это часть плоскости, которая ограничена замкнутой ломанной.

Геометрия многоугольников

В целом такая геометрическая фигура может иметь абсолютно любой вид. К примеру, символы звезды и компаса, полигон для моделирования или грань шестеренки — многоугольники. Многоугольные фигуры разделяются на две группы:

Выпуклый полигон, у которого все углы равны и все стороны равны, считается правильным и имеет собственное название. К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон. Любой правильный многоугольник имеет свою вписанную и описанную окружность. При этом круг также можно представить как правильный полигон, который имеет бесконечное количество углов.

Многоугольники в реальности

Невыпуклые многоугольники практически не распространены в реальной жизни: они довольно редко встречаются в природе, а в рукотворном виде она выступают в роли граней деталей машин. Многие морские организмы обладают пентасимметрией, и наиболее очевидным примером невыпуклой фигуры является морская звезда.

Правильные геометрические фигуры наоборот широко встречаются в природе. Наиболее очевидным примером являются пчелиные соты, каждая ячейка которых представляет собой гексагон. Такие гексагональные ячейки позволяют маленьким труженицам наиболее экономно использовать площадь улья, заполняя пространство без просветов. Кроме того, многие простейшие организмы, например радиолярии, имеют форму правильных полигонов.

Площадь многоугольника

Площадь геометрической фигуры — это характеристика плоского объекта, которая показывает его размер. Площадь невыпуклых многоугольников находится путем разбиения фигуры на более мелкие составляющие, обычно треугольники или квадраты. Наш онлайн-калькулятор позволяет вычислять площадь только правильных многоугольников, которая определяется общей формулой:

S = n/4 × a 2 × ctg(pi/n),

где n — количество сторон фигуры, a — длина стороны.

Так как около любого правильного полигона можно описать окружность или вписать ее в него, мы можем использовать соответствующие радиусы для вычисления площадей многоугольников. Сторона и радиус описанной окружности для любого полигона соотносятся как:

где R – радиус описанной окружности, n – количество сторон геометрической фигуры.

Для вписанной в полигон окружности соотношение немного изменяется и выглядит как:

где r – радиус вписанной окружности.

Таким образом, для определения площади любого правильного полигона вам понадобится указать количество сторон n и любой параметр на выбор:

Рассмотрим пару примеров для нахождения площади любого многоугольника.

Примеры из жизни

Пчелиные соты

Пчелиные соты — уникальный природный объект, который состоит из множества гексагональных призматических ячеек. Давайте подсчитаем, сколько таких шестиугольников находится в одних сотах. Для этого нам нужно узнать общую площадь и площадь одной ячейки. Из Википедии мы знаем, что стандартная рамка для сот имеет размеры 435 х 300 мм, соответственно, общая площадь составляет 130 500 квадратных миллиметров. Там же указано, что горизонтальный диаметр одной ячейки составляет примерно 5,5 мм. Горизонтальный диаметр полигона — это диаметр вписанной в него окружности, следовательно, мы знаем параметр r = 2,75 мм. Таким образом, при n = 6 площадь одной ячейки составляет:

Теперь мы можем узнать общее количество ячеек в одних сотах, которое выражается как 130500/26,19 = 4982

Снежинка

Снежинки имеют форму правильного треугольника или шестиугольника благодаря тому факту, что вода состоит из трех атомов и при переходе из одного агрегатного состояния в другое, молекулы воды соединяются с другими частицами и образуют треугольник или гексагон. Равносторонний треугольник — это такой же правильный полигон, как и другие, ведь он имеет три равных стороны и три равных угла. Соответственно, мы можем определить площадь такой снежинки, зная только длину стороны. Пусть сторона снежинки равна 8 условным единицам. Тогда для определения площади нам потребуется указать n = 3 и a = 8. Мы получим результат в виде:

Кроме площади абстрактной снежинки, наш калькулятор посчитал также радиусы вписанной и описанной окружности.

Заключение

Правильный полигон — это не только экзотический додекагон, но и квадрат или равносторонний треугольник, а значит, такую фигуру вы обязательно встретите не только в школьных задачах, но и в быту, на работе и в реальной повседневности. Используйте наш калькулятор для определения площадей любых правильных многоугольников.

Источник